收入与消费关系的再认识
——基于函数性典型相关分析的研究
靳刘蕊
(河南财经学院统计学系,河南 郑州 450002)
收入与消费关系的再认识
——基于函数性典型相关分析的研究
靳刘蕊
(河南财经学院统计学系,河南 郑州 450002)
将函数性典型相关分析方法应用于城镇居民家庭人均可支配收入与消费性支出的共变模式研究,发现城镇居民家庭收入和消费之间的相关形式在不同收入的地区之间存在着差异,不同收入水平的地区应实施不同的收入和消费政策。同时,通过研究也验证了函数性典型相关分析方法在经济数据分析中具有良好的性质,可挖掘出一些用传统方法不易识别的经济规律。
消费函数;面板数据;曲线相关;典型相关分析
一、引 言
改革开放以来,随着我国社会经济的迅速发展,居民的收入水平和消费水平都在不断地提高。同时,人民生活消费水平的提高又是促进社会经济持续健康发展的根本动力。在世界经济增长速度放缓,内需主导经济增长的格局进一步强化的条件下,着力促进消费需求的增长是实现国民经济持续健康快速发展的必然选择。因此,研究收入与消费之间的关系,对制定有效的消费政策和促进经济增长有着特殊的经济意义。
在收入与消费之间关系的研究文献中,绝大多数文献着力于研究收入对消费的单向影响关系——消费函数的表现形式。例如,最有代表性的是凯恩斯提出的绝对收入假说、杜森贝利提出的相对收入假说、莫迪利安尼等提出的生命周期假说、弗里德曼提出的持久收入假说等;随着现代各种经济理论和计量分析工具的发展与应用,消费函数理论及其研究成果层出不穷(郭新华等,2006)。以上研究成果具有内容的抽象性和适用对象的普遍性等特点,尤其是最有代表性的消费函数在经济学发展史上具有重要的意义。
毫无疑问,收入是影响消费的决定性因素,但同时,消费通过促进经济发展也影响着收入,收入与消费的关系是双向共变的。对于不同收入水平的地区,收入与消费之间的相关关系和共变模式是否相同?如果不同,那么不同收入水平的地区是否应根据本地区收入与消费的变化模式来制定和实施不同的收入和消费政策。为此笔者引入函数性典型相关分析方法对收入与消费的相关关系进行研究。函数性典型相关分析(FCCA)可用于研究两组曲线或时间数列相互关联的主要变化模式以及关联程度。
二、函数性典型相关的构建和算法
传统的典型相关分析(CCA)可以根据截面数据研究两组传统变量之间的相关关系,但却无法根据面板数据对两个函数性变量进行类似分析,函数性典型相关分析解决了此类问题。函数性典型相关分析的思想与传统多元统计分析中的典型相关分析的思想相同(朱建平,2006),但由于其分析对象是两个函数性变量,从而在算法上与传统典型相关分析算法有所不同。
(一)函数性典型相关的构建
假设对两个函数X、Y在时间t的某个有限区间T内进行N次观测,得到N对观测曲线(Xi,Yi),i=1,2,…,N。设ξ和η表示典型变量权重函数。假设总体均值曲线已知,并已经在观测数据曲线中减去了均值曲线,则样本方差和协方差曲线可表示为:

定义相应的算子 v11、v22、v12,f表示一个 t的函数,v11f表示为:

相应地定义 V11、V12。典型变量(ξ,Xi)与(η,Yi)的样本相关系数的平方用ccorsq(ξ,η)表示:

对于第一对典型变量的求解,直觉的方法就是简单地寻找函数ξ1和η1使ccorsq(ξ,η)最大化。这等同于求解以下约束条件下的最大化问题:
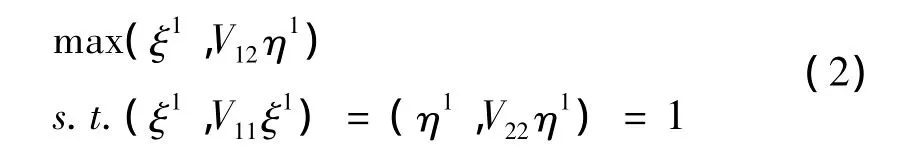
但是,从理论结果和实例来看,(2)式的最大化求解并不能得到关于数据或模型的任何有意义的信息。假设z1,…,zn是任意的实数向量,在函数典型相关分析中为了克服由函数性数据的高维引起的计算崩溃问题,克服在无限维数据中不存在相应的自协方差算子及其逆矩阵的问题,克服总能够找到典型权重函数使典型相关等于1的问题等,必须施加正则化(Brumback et al,1998)。对于某个常数αx,存在函数ξ使得对于所有的 i有 zi= αx+(ξ,Xi)。同样,对于某个常数αy,存在函数η使得对于所有的i有zi=αx+(η,Xi)。这意味着既可以利用Xi也可以用Yi对给定的zi做出完全预测。因此,不仅可以找到使ccorsq(ξ,η)=1的ξ和η(因为(ξ,Xi)和(η,Yi)完全相关),而且可以将作为典型变量的zi取任何值,包括常数。从这种意义上来说,任何可能的函数都可以作为具有完全相关性的典型变量权重向量(Davidian et al,2004)。为了得到有意义的结果,典型变量权重函数的求解过程必须施加正则化,主要方法是粗糙惩罚法。用二阶导数积分的平方‖D2f‖2来量化粗糙程度,并在适当的情况下施加周期性边界条件。典型相关分析引入平滑的方式是在约束项中加入粗糙惩罚项,类似于岭回归技术。形式为:

如果函数f和g满足适当的边界条件,据分步积分法可推导出(D2f,D2g)=(f,D4g),因此,有‖D2f‖2=(D2f,D2f)=(f,D4f)。所以上式等同于:

通过在约束项中加入粗糙惩罚项,在评估特定的候选典型变量时,不仅仅要考虑其方差,还要考虑其粗糙性,因此,(3)式所示问题等同于对惩罚样本相关系数平方的最大化问题:

称(4)式的求解过程为平滑典型相关分析。
与经典典型相关分析类似,使(4)式最大化的函数(ξ1,η1)是方程组

的最大正特征值ρ1对应的特征函数。第一对典型变量(ξ1,Xi)和(η1,Yi)的相关系数为。
平滑参数λ1和λ2的值越大,表明对粗糙惩罚越重视,而对平滑典型相关分析得到的典型变量的真实相关性重视得越少。要得到既具有适当平滑的权重函数又具有合理的相关系数的这样一对典型变量,必须选择合适的平滑参数。一般地,仅考虑λ1=λ2=λ的特殊情况对解决一般的问题就足够充分了。平滑参数可以主观地选取,也可以采用自动化过程选取,例如交叉确认法。
若第一对典型变量不足以代表两个原始函数X和Y,则可求其次要的典型变量。方程组(5)的最大特征值之后的其他正特征值及其对应的特征函数给出了次要的典型相关系数及典型变量的权重函数。这些特征函数关于惩罚样本协方差算子V11+λ1D4、V22+λ2D4正交,而不是关于原样本协方差算子正交。可采用与计算第一对典型变量时相同的平滑参数计算次要典型变量相关系数。
(二)函数性典型相关分析算法
实际中,可以用多种数值方式实现平滑的函数典型相关分析,主要有三种方法:离散化法、基函数法和对典型变量粗糙惩罚法(Ramsay,2005)。
1.离散化法。用细网格将函数ξ、η和协方差算子vjk(s,t)离散化,用一个有限的差分近似替代算子D4。方程组(5)就变成一个大的线性方程组,其第一特征值和特征向量可以用标准的数值方法解出。
2.基函数方法。对函数 Xi、Yi和权重函数 ξ、η用同一个基展开。设 φ1,φ2,…,φm为一个合适的基,K 是元素为(D2φj,D2φk)的矩阵,J 是元素为(φj,φk)的矩阵。如果是傅立叶基或其他正交基,则J是单位阵。定义C和D分别为Xi和Yi的基展开系数矩阵,有。以 a和b分别表示函数ξ、η的基展开系数向量。定义、和为数据基展开对应的样本M×M方差和协方差矩阵,其(v,ρ)元素分别为。在基展开情况下,给定数据的平滑典型相关问题转化为求解下面方程组的特征值问题:

基函数的数目M应足够大,以保证是通过平滑参数λ而不是维度M来对正则化进行控制。根据经验,M值大约为20时可有好的结果,且不会引起过度的计算负担。
3.粗糙惩罚法。设zi=(ξ,Xi)是一个可能的典型变量。可定义一个矩阵RX来衡量变量zi基于函数变量 Xi的粗糙程度,即 ‖D2ξ‖2=z'RXz。同样,设wi=(η,Yi),定义矩阵RY用来衡量变量wi基于函数变量 Yi的粗糙程度,即 ‖D2η‖2=w'RYw。其中,RX和 RY为 Moore-Penrose广义逆矩阵。这样,平滑典型相关方法可转化为下面的问题:
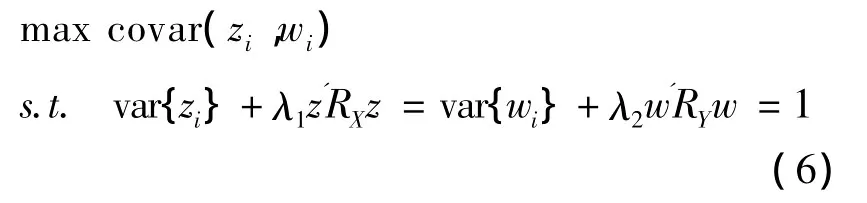
简化求解(6)式的复杂性,问题转化为求解下面的特征值问题:

对(7)式左乘[z'w'],整理可知,(7)式的任何解都满足

所以,│ρ│≤1。由于常数向量的最光滑函数内插的粗糙程度为零,RX1=RY1=0,所以(7)式第一对典型变量为常数z=w=1,对应的特征值为ρ=1,应该被忽略。求解(7)式的第二大特征值时,还要满足附加约束。
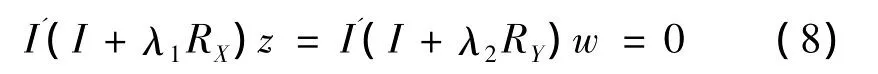
因此,(7)式的第二个及随后的特征解是我们要求的典型变量,且自动地满足样本均值为0的条件。
三、中国城镇人均可支配收入与消费性支出关系的再认识
本文利用1998年~2008年我国29个地区城镇居民家庭的人均可支配收入和人均消费性支出的面板数据,研究我国城镇居民家庭人均可支配收入与消费性支出之间的相关关系。
为了排除不同地区由于经济发展程度不同的影响,从总体上反映城镇居民家庭的人均可支配性收入和人均消费性支出之间的关系,计算29个地区人均可支配收入和人均消费性支出的平均曲线以及其一阶、二阶导数曲线,如图2所示。从总体来看,人均可支配性收入和人均消费性支出的变化趋势大致相同:由平均曲线可知,在观察期内人均可支配收入高于人均消费性支出,它们同时随着时间的迁移而持续增长;由一阶导数曲线可知,人均可支配收入的增长速度始终快于人均消费性支出的增长速度,在1995年~1997年间它们的增长速度都是减缓的,1997年之后增长速度又都持续加快;由二阶导数曲线可知,在1995年~1997年间它们的增长速度减缓的速度逐渐下降,人均消费性支出的增长速度减缓的速度慢于人均可支配收入,1998年~2005年期间两者增长速度加快,且人均可支配收入的增长速度加快的速度高于人均消费性支出。

图1 我国29个地区城镇家庭人均可支配收入和消费性支出
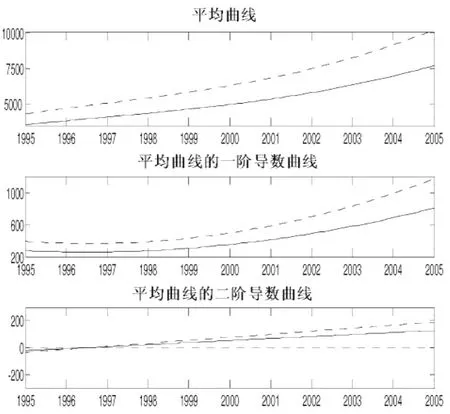
图2 我国29个地区城镇家庭平均人均可支配收入和消费性支出的平均曲线及其一阶、二阶导数曲线
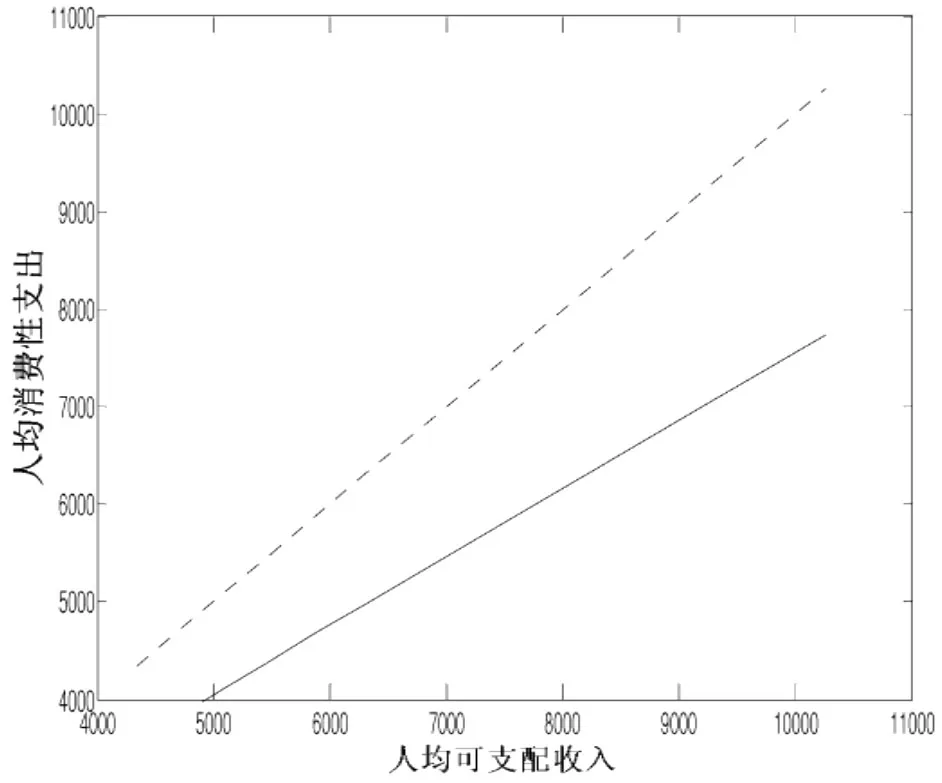
图3 城镇家庭平均人均消费性支出相对于平均人均可支配收入的曲线

图4 城镇家庭人均可支配收入和消费性支出的第一对典型变量权重函数
图3中虚线代表人均消费性支出等于可支配收入的状况,实线代表1995年~2005年期间实际的平均人均消费性支出相对于平均人均可支配收入的状况,由图可以看出,平均人均消费性支出占平均人均可支配收入的比重随着时间迁移有逐渐地缓慢下降趋势。
下面根据中心化后的人均消费性支出和人均可支配收入曲线的方差协方差函数,采用二阶导数积分的平方作为惩罚项来计算两者的典型变量权重函数,其中平滑参数由交叉确认方法确定。图4~图6为前三对相关性较强的典型变量的权重函数图,表1为29个地区对应的典型变量得分。
图4为第一对典型变量权重函数,可以看出两条曲线非常相似,在1995年~2005年期间,人均可支配收入的典型变量权重函数的变化先于人均消费性支出,这意味着在此期间人均可支配收入偏离平均水平之后接着出现了人均消费性支出的相应变动。从1995年到1998年,第一对典型变量权重函数都小于零,但不断增大,说明两个变量都低于平均水平,且低于平均水平的程度逐渐减小;此后到2000年期间,权重函数都大于零,但经历了先增长后下降的趋势,说明两个变量在该期间都高于平均水平,但高于平均水平的程度先增加后减少;从2000年到2004年,两个变量都低于平均水平,且2002年到2003年之间低于平均水平的程度逐渐增大,2003年到2004年之间低于平均水平的程度又逐渐减小;2004年之后,两个变量都高于平均水平,且高于平均水平的程度迅速增大。第一对典型变量之间的典型相关系数的平方为0.9955,说明两个变量之间的这种变化模式具有很高的相关性。从表1可知,河北、山西、内蒙古、辽宁、吉林和四川等17个地区在第一对典型变量上得分较高,表明在这些人均可支配收入和人均消费性支出较低的地区,两者之间随时间变化的相关关系主要遵循图4所示的模式,人均可支配收入偏离平均水平之后很快就出现人均消费性支出的变动,且变动程度大致相同。
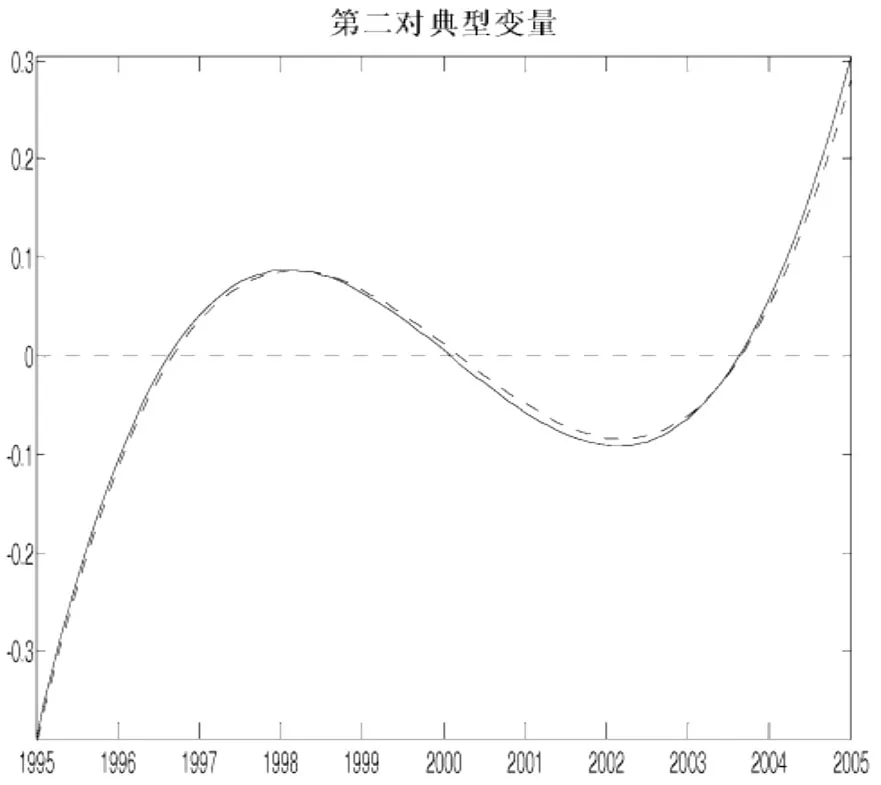
图5 城镇家庭人均可支配收入和消费性支出的第二对典型变量权重函数

图6 城镇家庭人均可支配收入和消费性支出的第三对典型变量权重函数
由图5第二对典型变量权重函数可以看出,它们也非常相似,但与第一对典型变量权重函数的变化大致相反,但波动程度较大。人均消费性支出的典型变量权重函数的变化先于人均可支配收入权重函数的变化,但时间差很小。第二对典型变量在1995年到1997年期间,两个变量低于平均水平,但低于平均水平的程度逐渐减小;此后到2000年期间,两个变量高于平均水平且高于平均水平的程度先逐渐增大,1998年达到极大值点后逐渐减小;从2000年到2004年,两个变量都低于平均水平,其中2000年到2002年低于平均水平的程度逐渐增大,2003年到2004年低于平均水平的程度又逐渐减小;2004年之后,两个变量都高于平均水平,且高于平均水平的程度迅速增大。第二对典型变量之间的相关系数的平方为0.9968,说明两个变量之间的这种变化模式也具有很高的相关性。从表1中可知,北京、上海、浙江、山东和福建等5个地区在第二对典型变量上得分较高,表明在这些人均可支配收入和人均消费性支出较高的地区,两者之间随时间变化的相关关系主要遵循图5所示的模式,这些地区支出的高度变动几乎与收入同时发生且变动程度也大致相同,支出的变动稍微领先于收入,可以认为对于人均可支配收入比较高的地区,消费的增加在一定程度上促使了收入的增加。
由图6第三对典型变量权重函数可以看出,1995年~2005年期间,人均可支配收入的典型变量权重函数的变化先于人均消费性支出的变化,同样意味着在此期间人均可支配收入高度变动之后接着出现人均消费性支出的高度变动。与第一对典型变量相比较,第三对典型变量中,人均消费性支出变动滞后于人均可支配收入变动的时间较长,且变动程度较大。第三对典型变量之间的相关系数的平方为0.8381,说明两个变量之间的这种变化模式也具有较高的相关性。由表1可知,天津、广东、江苏、安徽、湖南、广西和云南等7个地区在第三对典型变量上得分较高,表明在这些人均可支配收入和人均消费性支出处于中等水平的地区,两者之间随时间变化的相关关系主要遵循图6所示的模式,这些地区支出的高度变动稍微滞后于收入的变动,由此可以认为对于人均可支配收入中等的地区,收入的增加会促使消费在一定时间之后增加。
通过以上描述性分析和函数性典型相关分析,可以看出我国29个地区城镇居民家庭的人均可支配收入和人均消费性支出之间有着高度的相关性,但随着时间发展的相关形式在不同人均可支配收入的地区之间存在着差异。随着经济的发展,不同地区的消费群体其消费水平以不同的形式变化,给未来市场带来新的发展机遇。在可支配收入水平较高的地区,消费性支出的变化不完全是收入变化的结果,相反消费水平的提高可能会促使收入的增加,因此扩大消费品的种类和提高消费品的质量可能促使该地区的内需增加;在可支配收入处于中等和较低水平的地区,提高居民的收入水平能促使消费的增加,从而促使该地区的内需增加。
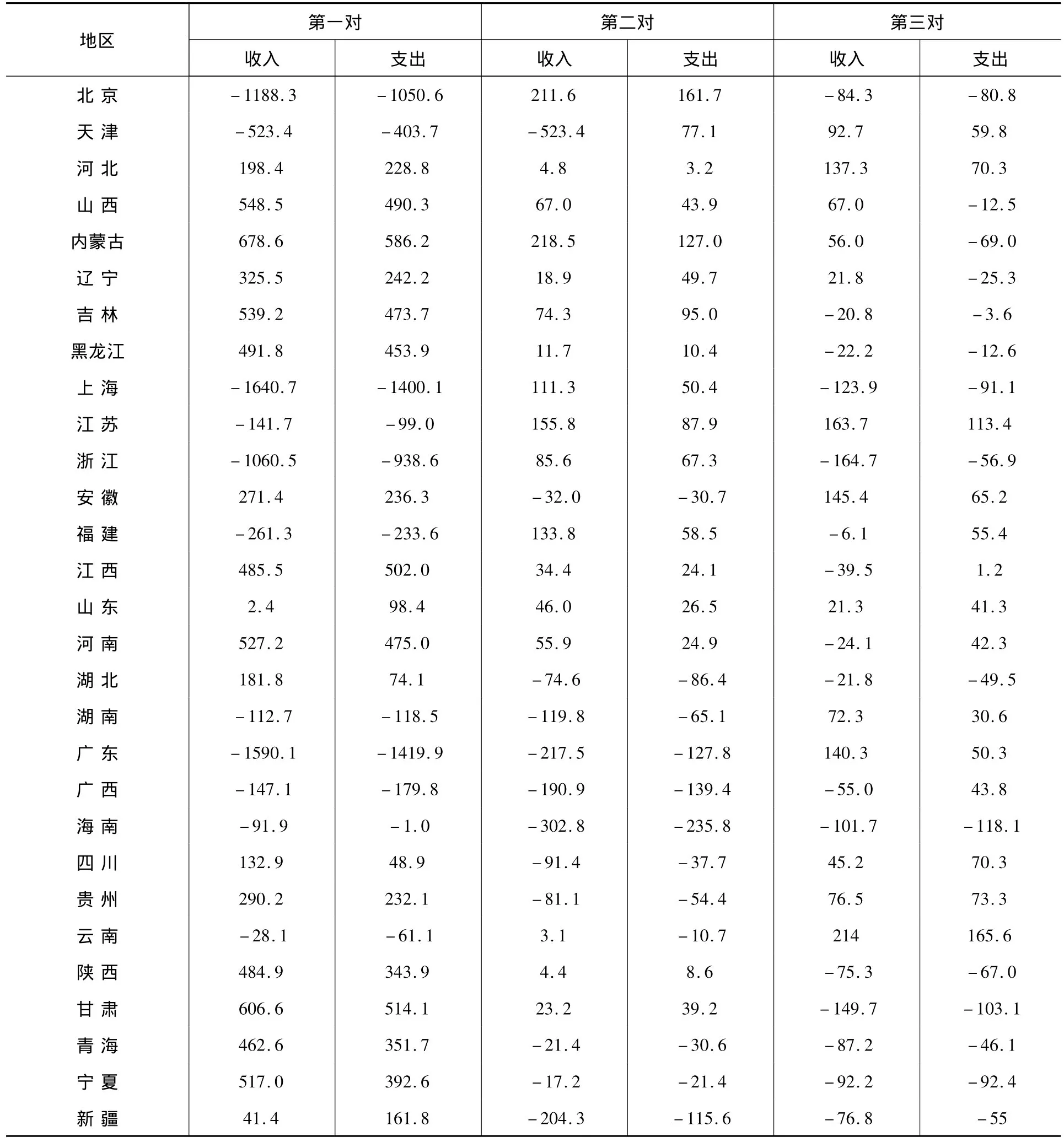
表1 典型相关得分
四、结 论
随着经济的发展,不同地区的消费群体其消费水平以不同的形式变化,给未来市场带来新的发展机遇。鉴于以上研究,为了扩大内需,不同收入水平的地区应实施不同的收入和消费政策,例如,在可支配收入水平较高的地区,提高居民收入的同时,扩大消费品的种类和提高消费品的质量也能促使该地区的内需增加;在可支配收入处于中等和较低水平的地区,提高居民的收入水平是促使消费增加、进而扩大内需的最有效办法。
此外,随着技术的进步,各领域测度和记录越来越多的函数性数据。相对于传统的数据分析方法,函数性数据分析从函数的视角提供了数据分析的新思路和方法(严明义,2007),可以对数据挖掘出更多的潜在的、不易识别或度量的发展变化模式和信息。函数性典型相关分析是对函数性数据进行分析的一种方法,具有区别与传统典型相关分析方法的独特优势,在经济数据分析中具有重要的现实意义和广阔的应用前景。
[1]郭新华,李勇辉,伍再华.现代西方消费函数理论前沿与发展研究[J].生产力研究,2006,(1):235-237.
[2]严明义.函数性数据的统计分析:思想、方法和应用[J].统计研究,2007,(2):87 -94.
[3]朱建平.应用多元统计分析[M].北京:科学出版社,2006.
[4]Brumback B A,Rice J A.Smoothing spline models for the analysis of nested and crossed samples of curves(with Discussion)[J].Journal of the American Statistical Association,1998,(93):961-994.
[5]Davidian M,Lin X,Wang J L.Introduction Emerging Issues in longitudinal and Functional Data Analysis[J].Statistical Sinica,2004,(14):613 -614.
[6]Ramsey J O.Functional components of variation in handwriting[J].Journal of the American Statistical Association,2000,(92):9 -15.
[7]Ramsay J,Silverman B.Functional data analysis[M].New York Springer,2005.
Rethink the Relationship Between Income and Expenditure
JIN Liu-rui
(Statistics Department,Henan University of Finance and Economics,Zhengzhou 450002,China)
In the paper the method of functional canonical correlation analysis(FCCA)is applied into analyzing covering models between annual income per capita and living expenditure of urban households.We find that there are different relation modes between income and consumption in different regions.And then,we verify that FCCA has good properties and significance in analyzing economic data and can mine economic laws which cannot be easily found with traditional methods.
consumption function;panel data;correlation between curves;canonical correlation analysis
F014.5
A
1007-9734(2010)04-0020-07
2010-04-15
靳刘蕊,女,河南辉县人,博士,研究方向为多元统计分析和数据挖掘。
责任编校:陈 强,王彩红

