钻井液压力多进制相移键控信号的数值建模及特性分析

沈 跃，李 翠，朱 军，苏义脑，李 林

（1.中国石油大学物理科学与技术学院，山东东营 257061;2.中石油钻井工程技术研究院，北京 100083）

钻井液压力多进制相移键控信号的数值建模及特性分析

沈 跃1，李 翠1，朱 军1，苏义脑2，李 林2

（1.中国石油大学物理科学与技术学院，山东东营 257061;2.中石油钻井工程技术研究院，北京 100083）

通过理论建模和数值分析研究3种钻井液压力多进制相移键控（MPSK）调制方式应用于钻井液压力信号传输的可行性。利用二进制数据中相邻两位码元的组合形成携带四进制信息的数字基带控制信号，建立脉宽及脉位钻井液压力多进制相移键控调制以及正交相移键控（QPSK）多进制调制的旋转阀控制逻辑规则。通过构建钻井液压力多进制相移键控信号数学模型，研究3种MPSK信号的频域特性和传输特性。数值分析表明:由于脉位MPSK和QPSK调制方式带宽内信号能量比较大，适于数据传输;在井筒参数和载频相同条件下，钻井液信道对QPSK信号传输的影响要大于脉位MPSK调制，但从旋转阀转速控制角度分析，QPSK相对于脉位MPSK调制更容易实现，只是信号的检测和数据恢复技术相对要求较高。

随钻测井;钻井液压力;多进制相移键控;数学模型;特性分析;数值计算;信号

地质导向钻井及闭环钻井等现代钻井技术需要较高的井下信息传输速率［1-2］。目前先进的钻井液信息遥测系统均采用连续压力波技术结合钻井液压力多进制相移键控调制技术，以频带方式进行数据传输［3］，钻井液压力调制通常分为二进制差分相移键控（DPSK）调制［4-5］及多进制相移键控（MPSK）调制，MPSK调制在与DPSK相同载频和信号带宽下可以成倍提高信息传输速率，例如，Schlumberger公司的PowerPulse旋转阀系统，采用四进制的正交相移键控（QPSK）方式进行钻井液压力调制，信息传输速率达到16 bit/s。由于目前采用的钻井液压力MPSK调制技术仅限于QPSK方式，其他基于钻井液压力的MPSK调制方法与QPSK方式相比有何特点及可行性研究还未见报道，笔者通过构建钻井液压力MPSK信号的数学模型，研究3种MPSK调制方式应用于钻井液压力信号传输的可行性。

1 钻井液压力MPSK信号数学建模

1.1 多进制相移键控调制的旋转阀控制逻辑规则

根据数字通信理论，每个二进制位为一个二进制码元，多个相邻的二进制码元可组成一位多进制码元，由于多进制码元携带的信息量大，有利于提高通信系统的传输效率。钻井液压力的多进制相移键控（MPSK）调制利用载波的4种相位状态来代表四进制信息，通过二进制数据中相邻两位码元的组合形成携带四进制信息的数字基带信号，数字基带信号作用于载波相位实现相移键控调制［6］。数字基带信号以比特（bit）周期构成，载波相位受调制后，MPSK信号的一个比特周期由4个载波周期组成［7］。QPSK信号的产生通过编码数字基带信号构成一个脉宽为Tc的可变幅度逻辑控制脉冲序列LQPSK（t）作用在旋转阀电机上，通过在比特周期的第一个载波周期时间内降低旋转阀转速对压力载波进行四进制键控移相。脉位MPSK调制的钻井液压力MPSK信号产生是通过编码数字基带信号构成一个脉宽为Tc的固定幅度逻辑控制脉冲序列LMPSKP（t）作用在旋转阀电机上，通过在比特周期内某一位置的载波周期内降低旋转阀转速一半对压力载波进行四进制键控移相。脉宽MPSK调制的钻井液压力MPSK信号产生是通过编码数字基带信号构成一个宽度为k1Tc（k1为四进制码元值）的固定幅度逻辑控制脉冲序列LMPSKW（t）作用在旋转阀电机上，通过在比特周期内前k1个载波周期降低旋转阀转速一半对压力载波进行四进制键控移相。因此，对于某一个二进制编码数据，将其用四进制描述后依据不同的MPSK调制规则会产生3种数字基带信号，见图1。

根据信号相位与角频率关系θ（t）=ωnt，在基带脉冲宽度Tp内通过降低旋转阀转速使压力载波产生的相位滞后或相移为

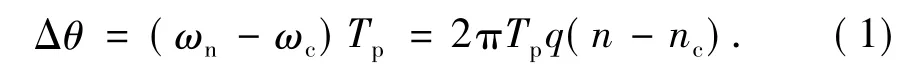
式中，ωn为基带脉冲作用下的载波角频率;ωc为无基带脉冲时载波角频率;n为基带脉冲作用下的旋转阀转速;nc为无基带脉冲时旋转阀转速;q为旋转阀的阀孔数。遵循通信理论的2π/M信号矢量分配规则［8］，旋转阀的控制逻辑规则见表1。

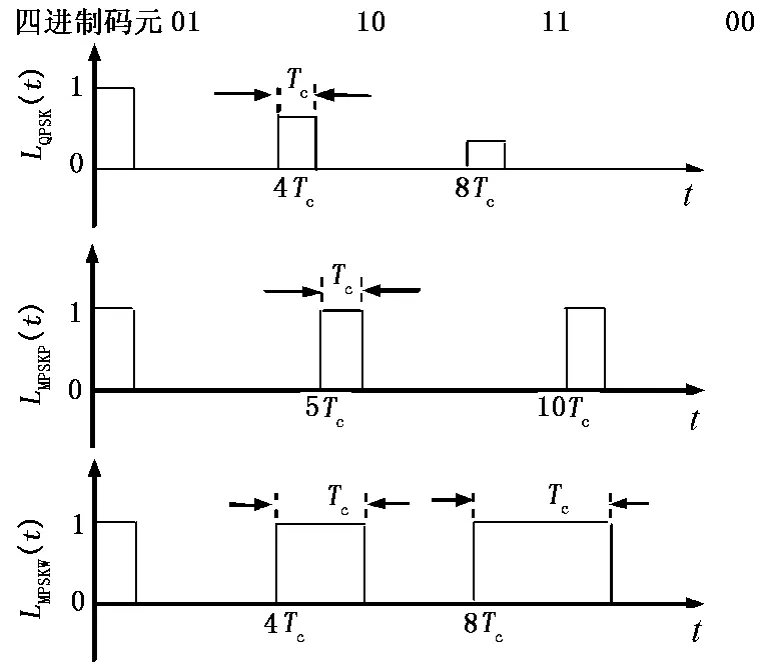
图1 旋转阀控制数字基带信号Fig.1 Digital baseband signal for rotary valve control

表1 多进制相移键控调制的旋转阀控制逻辑规则Table 1 Rotary valve control logic rule of MPSK modulation

1.2 数学建模

根据通信原理，在数字调制信号作用下，钻井液压力MPSK信号可表示为［9］

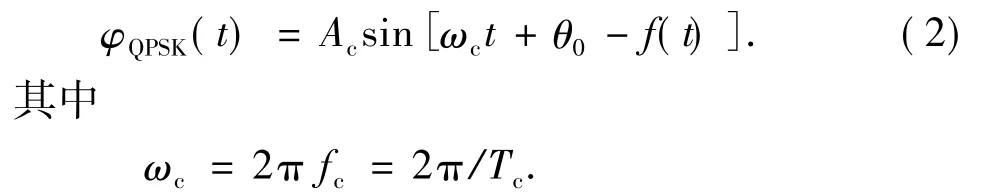
式中，Ac为压力载波幅度，Pa;θ0为载波初相位，（°）;f（t）为与数字调制信号有关的相移函数。

以10位二进制数进行多进制相移键控调制为例，设数据编码为C=c10c9c8c7c6c5c4c3c2c1，其中cn为二进制码元，将C分为5组，每组的两位二进制码元ambm可组合成四进制码元dm=ambm，则数据编码又可表示为

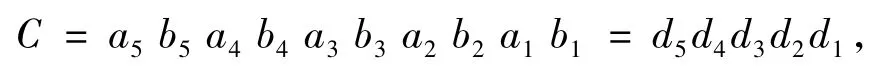
其中dm有00，01，10，11四种状态，m=1，2，…，5。当四进制码元由d1→d5顺序传送时，即构成图1所示的数字基带信号。

1.2.1 QPSK信号数学模型

设可变幅度单脉冲函数为

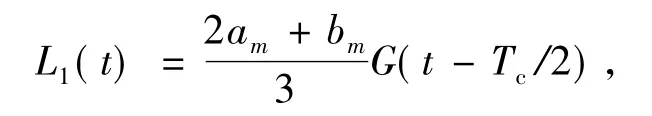
其中G（t）为门函数，根据信号的数学分析，在可变幅度单脉冲作用下的相移函数为

由于f1（t）为分段函数，需通过傅里叶正、逆变换转换成连续函数。由G（t）的频谱密度函数G（jω）=TcSa（ωTc/2），根据傅里叶变换的时移特性，对L1（t）进行傅里叶变换得

根据傅里叶变换的时域积分性质得f1（t）的频谱密度函数为

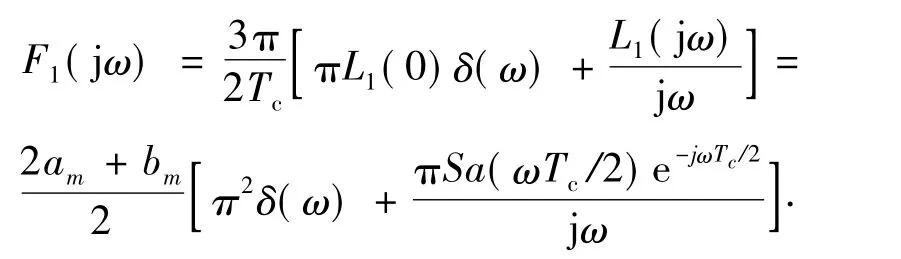
对F1（jω）进行傅里叶逆变换得到单脉冲调相时的相移函数为

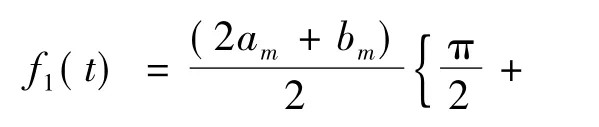
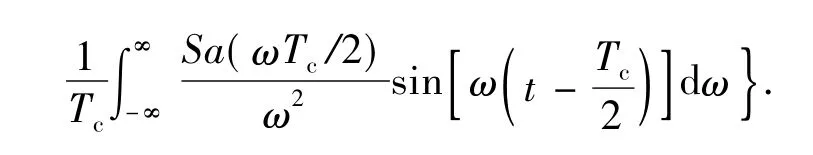
对于图1所示的数字基带信号LQPSK（t），每个四进制码元代表的脉冲在时间轴上间隔4Tc出现，相当于相对于第一个码元脉冲分别延迟了4（m－

1）Tc，脉冲幅度为（2am+bm）/3。因此QPSK调制的数字基带信号可表示为

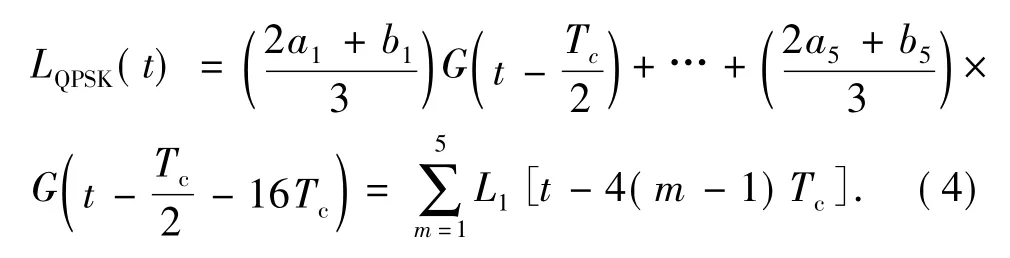
根据相移函数与调相数字基带信号的积分关系，通过傅里叶正、逆变换转换成连续函数得

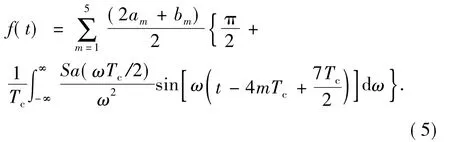
因此，由5位四进制码元构成的钻井液压力QPSK信号数学模型为

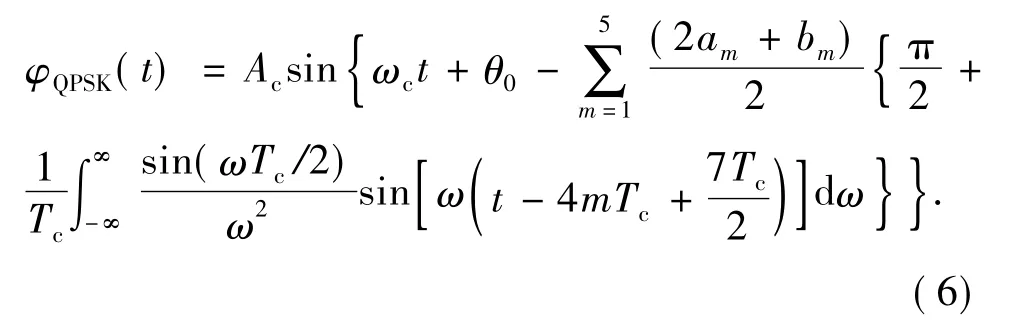
1.2.2 脉位MPSK调制的数学模型

对于图1所示的数字基带信号LMPSKP（t），每个四进制码元在时间轴上间隔4Tc出现，码元脉冲的位置与数据编码有关，以第一个码元位置为基准，码元脉冲相当于分别延迟［4（m－1）－（2am+bm－1）］Tc出现。设单脉冲函数为L1（t）=G（t－Tc/2），则脉位MPSK调制的数字基带信号可表示为

该函数只适用于调相过程，对于不发生调相的情况，即ambm=00时该函数不适用，故在编程运算时对ambm=00情况进行特殊处理。

根据相移函数f（t）与LMPSKP（t）的积分关系，利用傅里叶变换的时移性质和时域积分定理，通过傅里叶正、逆变换得到相移函数

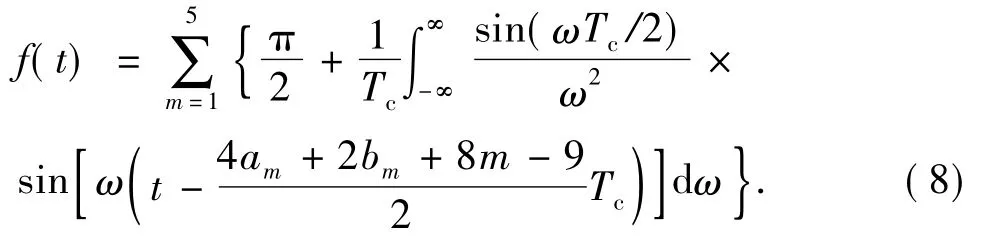
由5位四进制码元构成的脉位MPSK调制钻井液压力MPSK信号数学模型为

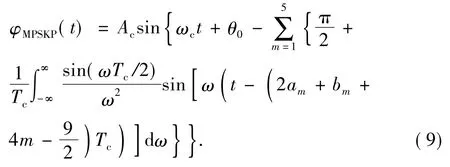
1.2.3 脉宽MPSK调制的数学模型

根据脉宽MPSK调制的钻井液压力调制规则，四进制码元产生的脉宽应使调制后的载波相位滞后（2am+bm）π，即脉冲宽度以标准单脉冲函数L1（t）=G（t－Tc/2）为基准沿时间坐标展宽，则脉宽MPSK调制的数字基带信号可表示为

在ambm=00情况下同样要进行特殊处理。根据相移函数f（t）与LMPSKW（t）的积分关系，利用傅里叶变换性质得到相移函数

由5位四进制码元构成的脉宽MPSK调制钻井液压力MPSK信号数学模型为

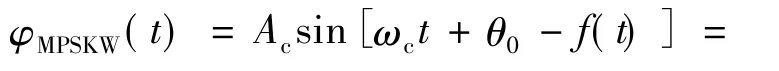
2 钻井液压力MPSK信号特性分析

2.1 频域特性

由于调制和传输过程中每种数据编码的出现具有随机性，以10位二进制数据转换为5位四进制数为例，数据编码有210=45=1024种组合，因此可以将已调钻井液压力信号看作随机信号，其平均功率谱密度［10］为

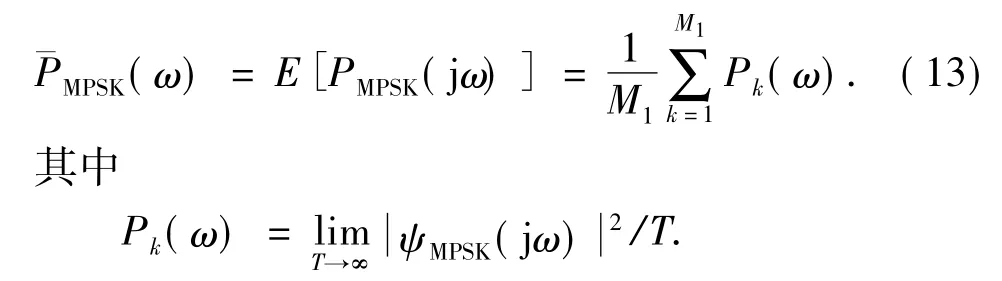
式中，Pk（ω）为第k个样本信号的功率谱密度函数;ψMPSK（jω）为φMPSK（t）的傅里叶变换;M1=1024为随机信号样本数。

图 2 为Ac=1，fc=20 Hz，θ0=0°条件下，由5位四进制码元组成的数据在3种多进制相移键控调制方式下产生的钻井液压力MPSK信号平均功率谱密度。

图2 钻井液压力MPSK信号平均功率谱密度Fig.2 Average power spectrume density of drilling fluid pressure MPSK signals

从图中看出，3种调制方式的平均功率谱密度（频谱）均存在明显频带，且相同载频下信号频谱的主瓣带宽均相同。其中QPSK和脉宽调制MPSK信号存在明显的主、副瓣，QPSK信号副瓣较小，脉宽调制MPSK信号副瓣较大，脉位调制MPSK信号频谱只能看出主瓣，但形状不规则。通常信号传输后只有主瓣带宽内的信号分量被接收到，如果副瓣过大将造成主瓣内信号能量的降低，使信号接收质量下降。根据通信原理，四进制相移键控调制的信息传输速率为载频的一半，因此3者的频带利用率相等，但带宽内信号分量占信号总能量的比率（信号能量比）有所区别，见表2。

由表2看出，相同载频下脉宽MPSK调制带宽内信号能量比远小于其他两种调制方式，表明经过相同传输距离后脉宽MPSK调制信号的接收质量相对要降低很多，从频谱角度看不能保证信号的有效传输;脉位MPSK调制及QPSK调制带宽内信号能量比相对较高，适用于井下数据的调制与传输，但从旋转阀转速控制角度分析，QPSK调制相对于脉位MPSK调制更容易实现。

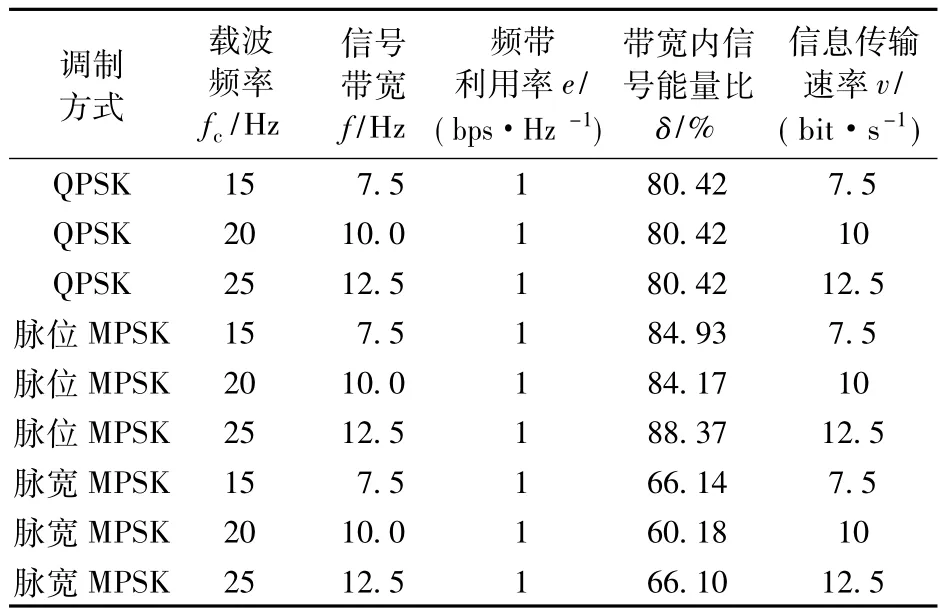
表2 钻井液压力MPSK信号的频域特性分析Table 2 Frequency domain characteristics analysis of drilling fluid pressure MPSK signals

2.2 传输特性

压力波信号在钻柱中传播时，由于钻柱特性、管壁对钻井液质点振动的阻碍、钻井液质点间的摩擦及钻井液压缩性的影响会产生信号传输的能量损失。

考虑压力信号在总井深为D的定向井中传输情况，将定向井钻柱分为垂直段OA、造斜段AB和水平段BC，压力波由井底经水平段传输至造斜段，然后进入垂直段钻柱到达井口。设:垂直段井深为DA，垂直段与造斜段井深之和为DB，造斜段钻柱曲率半径为R;将定向井钻柱均分成N段，每段长度为ΔD=D/N;井口钻井液温度为T0，井底钻井液温度为地层温度Td=0.03（DA+R），井温随定向井的垂深呈线性分布。对塑性钻井液流体应用伯努利方程，可得到任一井深处的压力和温度。

垂直段井深:

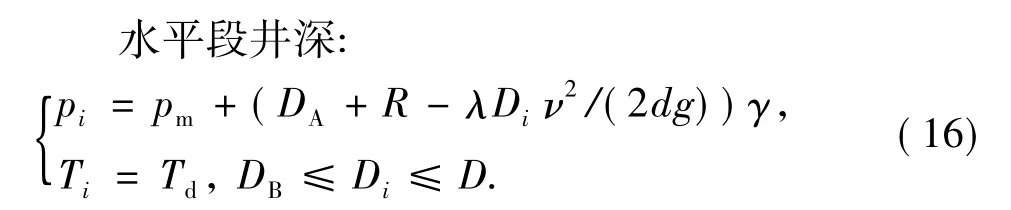
式中，pi为任一井深处钻井液压力;Ti为任一井深处钻井液温度;Di为任一井深;pm为井口泵压;λ为水力摩阻系数;ν为钻井液平均流速;γ=ρg为钻井液重度;ρ为钻井液密度。

根据钻井液压力波的传播特性方程［7］，得到任一井深处压力波的幅度为

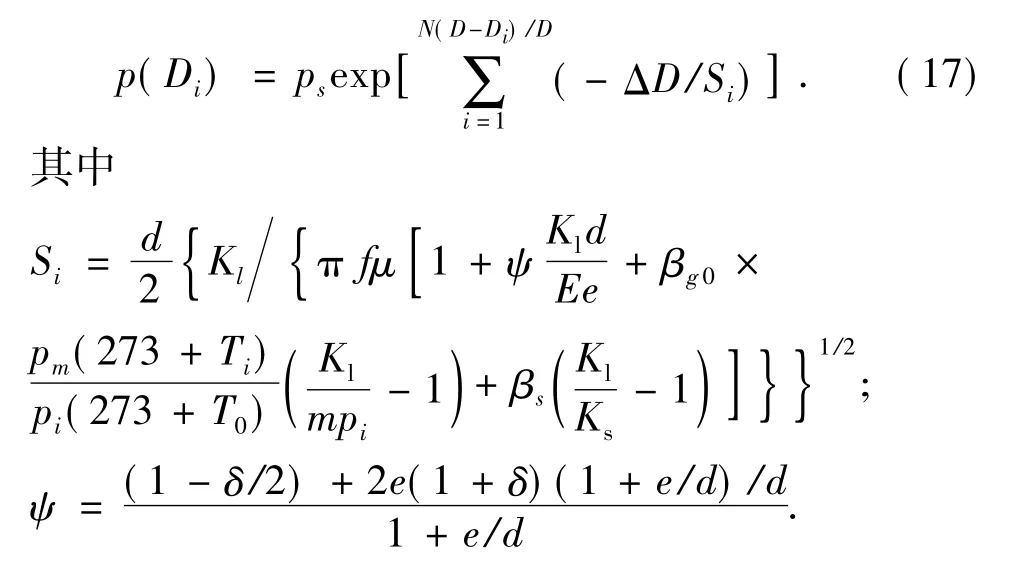
式中，ps为信号源压力;p（Di）为传输后在任一井深处的信号压力;Si为各段信道压力衰减指数［11-12］;βg0为井口钻井液含气率;m=1.2为气体比热容比;βs为钻井液中固相体积分数;Ks为钻井液固相体积弹性模量;Kl为液体弹性模量;E为钻柱弹性模量;e为钻柱壁厚;d为钻柱内径;δ为钻柱材料泊松比;μ为钻井液动力黏度;f为信号频率。

3 信号的时域仿真及传输特性分析

数值计算针对定向井情况，设:总井深3.225 km，其中垂直段井深2.0 km;造斜段井眼曲率半径143 m;造斜段井眼长度225 m;水平段长度1.0 km。根据文献［13］中提供的钻柱及钻井液参数:钻柱内径108.6 mm，壁厚9.2 mm，弹性模量2.1×105MPa，泊松比0.3;水基钻井液的固相体积分数15%，钻井液固相弹性模量16.18 GPa，钻井液动力黏度20 mPa·s，密度1 245 kg/m3，液体弹性模量2.04 GPa，井口钻井液含气率1%，井口钻井液温度30℃，流量30 L/s;井口泵压20 MPa;钻柱沿井深分成645段;载波幅度Ac=1 Pa，载频fc=20 Hz，初相θ0=0°;QPSK 调制数据编码为 C=1101100110，脉宽MPSK调制数据编码为C=0101010101，脉位MPSK调制数据编码为C=0001101100。数值分析表明，相应MPSK调制信号频谱的高频成分最丰富，钻井液信道对信号传输的影响最大。

3.1 信号的时域仿真与特性分析

根据钻井液压力MPSK信号数学模型，通过MATLAB 编程对 φQPSK，φMPSKW（t）和 φMPSKP（t）进行数值仿真，同时模拟出源信号传输全井段3.225 km距离后的信号波形，见图3～5。

图4 脉宽调制MPSK信号波形及随距离传输结果Fig.4 Waveform of MPSK signal based on PWM and transmitted results with propagation distance

图5 脉位调制MPSK信号波形及随距离传输结果Fig.5 Waveform of MPSK signal based on PPM and transmitted results with propagation distance

由图中源信号可以看出，3种MPSK调制信号波形均符合钻井液压力载波相位受码元控制的调制规律，说明通过相应的数字基带信号数学分析所建立MPSK信号数学模型的正确性。信号传输过程中由于存在能量损耗，信号幅度随传输距离逐渐减小;由于钻井液信道对信号不同频率成分的衰减程度不同，高频分量相对低频分量衰减更大，信号出现不同程度的失真。

3.2 信号传输特性及调制方式对信号传输的影响

设信号传递函数为钻井液信道某一井深处的信号幅度与源信号幅度之比，根据钻井液信道的传输特性分析，信号传递函数与传输距离、信号频率、井筒与钻井液参数有关。数值计算与分析表明，在载波频率、钻柱内径、钻井液黏度和含气率影响下，3种MPSK调制信号的传递函数随传输距离均呈近指数规律下降。3种MPSK调制信号的平均功率谱形状不同，说明频率分布是有差别的，如果信号频谱的高频成分越丰富，信道对信号的衰减程度越大。在信道参数和载频相同条件下，MPSK信号传输过程中信号传递函数随传输距离的变化曲线见图6。从图中可以看出，信道对脉宽与脉位MPSK信号传输的影响非常接近，对QPSK信号传输的影响要大于脉宽与脉位 MPSK信号。这一结果可以从3种MPSK调制信号的平均功率谱分析得出，通过数值计算，在 0～fc频带内 QPSK信号的能量比为59.33%，脉宽 MPSK调制信号的能量比为76.53%，脉位 MPSK调制信号的能量比为70.42%，说明QPSK信号频谱的高频分量相对比较丰富，信道对QPSK信号的衰减较大。

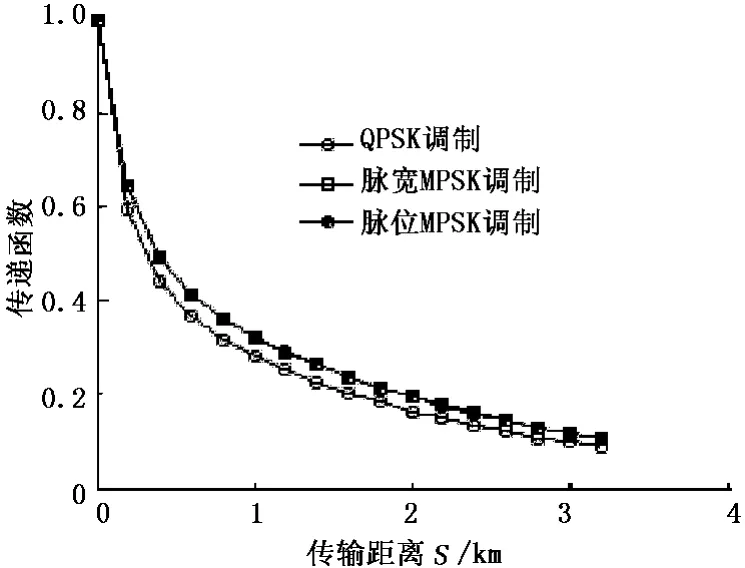
图6 调制方式对信号传输的影响Fig.6 Impacts of modulating type on signal propagation

载波频率的选取关系到井下信息的最大上传速率，在钻井过程中通常要根据不同的钻进深度、井筒参数和井眼轨道类型等来实时调整载波频率，以保证最大信息传输速率，因此如何确定最佳载波频率是非常关键的。通过钻井液压力MPSK信号的数学模型和式（17）的信号传递函数表达式，根据钻进过程中的钻柱和钻井液参数、井眼轨道类型、井深及地面可检测和处理的最小信号幅度，选择不同的频率值通过数值计算得到地面处的信号强度，然后用比对法可以确定出最佳参考载波频率。通过上述MPSK的信号特性分析编制相应的信号强度预测软件，可以为载波频率的合理选取提供参考依据。

4 结论

（1）根据多进制相移键控调制的旋转阀控制逻辑规则，通过数字基带信号控制旋转阀转速可以实现钻井液压力的MPSK调制。载波相位受码元调制的结果符合MPSK信号的调制规律，从而说明3种钻井液压力MPSK信号数学模型的正确性。

（2）脉位MPSK调制及QPSK调制带宽内信号能量比相对较高，适于井下数据的调制与传输，但从旋转阀转速控制角度分析，QPSK调制相对于脉位MPSK调制更容易实现，这是目前国外采用QPSK调制方式进行井下测量数据传输的主要原因。

（3）信道参数和载频相同条件下，钻井液信道对QPSK信号传输的影响要大于脉宽与脉位MPSK调制，因此对于钻井液压力QPSK信号的检测和数据恢复技术要求较高。

［1］ 张绍槐.现代导向钻井技术的新进展及发展方向［J］.石油学报，2003，24（3）:82-89.

ZHANG Shao-huai.New progress and development direction of modern steering drilling techniques［J］.Acta Petrolei Sinica，2003，24（3）:82-89.

［2］ 沈忠厚，黄洪春，高德利.世界钻井技术新进展及发展趋势分析［J］.中国石油大学学报:自然科学版，2009，33（4）:64-70.

SHEN Zhong-hou，HUANG Hong-chun，GAO De-li.A-nalysis on new development and development trend of worldwide drilling technology［J］.Journal of China University of Petroleum（Edition of Natural Science），2009，33（4）:64-70.

［3］ MARTIN C A，PHILO R M，DECKER D P，et al.Innovative advances in MWD［R］.SPE 27516，1994.

［4］ SHEN Yue，SU Yinao，LI Gensheng，et al.Numerical modeling of DPSK pressure signals and their transmission characteristics in mud channels［J］.Petroleum Science，2009，6（3）:266-270.

［5］ 沈跃，苏义脑，李林，等.钻井液连续压力波差分相移键控信号的传输特性分析［J］.石油学报，2009，30（4）:593-597.

SHEN Yue，SU Yi-nao，LI Lin，et al.Analysis on transmission characteristics of differential phase shift keying signal of continuous pressure wave in drilling fluid channel［J］.Acta Petrolei Sinica，2009，30（4）:593-597.

［6］ 王秉钧，冯玉珉，田宝玉.通信原理［M］.北京:清华大学出版社，2006:180-252.

［7］ HUTIN R，TENNET R W，KASHIKAR S V.New mud pulse telemetry techniques for deepwater applications and improved real-time data capabilities［R］.SPE 67762，2001.

［8］ 李宗豪.基本通信原理［M］.北京:北京邮电大学出版社，2006:365-370.

［9］ 江力，吴海红，严素清，等.通信原理［M］.北京:清华大学出版社，2007:36-38.

［10］ 周娟.信号分析与处理［M］.北京:机械工业出版社，2002:79-85.

［11］ 石在虹，刘修善.井筒中钻井信息的传输动态分析［J］.天然气工业，2002，22（5）:68-71.

SHI Zai-hong，LIU Xiu-shan.An analysis of drilling information transmission behavior in wellbore［J］.Natural Gas Industry，2002，22（5）:68-71

［12］ 何树山，刘修善.钻井液正脉冲信号的衰减分析［J］.钻采工艺，2001，24（6）:1-12.

HE Shu-shan，LIU Xiu-shan.Analysis of signal attenuation for positive drilling fluid pulse［J］.Drilling＆ Production Technology，2001，24（6）:1-12.

［13］ 刘修善，苏义脑.泥浆脉冲信号的传输速度研究［J］.石油钻探技术，2000，28（5）:24-26.

LIU Xiu-shan，SU Yi-nao.Study on transmission velocity of mud pulse signal［J］.Petroleum Drilling Techniques，2000，28（5）:24-26.

Numerical modeling and characteristics analysis of drilling fluid pressure MPSK signals

SHEN Yue1，LI Cui1，ZHU Jun1，SU Yi-nao2，LI Lin2

（1.College of Physics Science and Technology in China University of Petroleum，Dongying257061，China;2.CNPC Drilling Research Institute，Beijing100083，China）

The feasibility for the downhole data transmission of the drilling fluid pressure multiple phase shift keying（MPSK）modulation was researched by theoritical modeling and numerical analysis.The rotary valve control logic rules were built for drilling fluid pressure MPSK modulation based on the pulse width and pulse position control and the quadrature phase shift keying（QPSK）modulation by digital baseband control signal formed with the combination of adjacent double bits symbol in binary data.The frequency domain characteristics and transmission characteristics of the MPSK signals were studied by numerical modeling of the drilling fluid pressure MPSK signals.Numerical calculation results show that the MPSK signal based on pulse position modulation and the QPSK signal are fit for transmitting downhole data for their higher signal power in the bandwidth.The impacts on the QPSK signal transmission are greater than the MPSK signal based on pulse position modulation with the signal transfer function analysis in the condition of the same wellbore parameter and carrier frequency，but the QPSK modulation is correspondingly easy to be actualized by analysis of the rotary valve rotary speed control and better signal detecting and data recovering technology are needed in the QPSK signal processing.

logging while drilling;drilling fluid pressure;multiple phase shift keying（MPSK）;mathematical model;characteristic analysis;numerical calculation;signal

TE 927.6

A

10.3969/j.issn.1673-5005.2010.05.014

1673-5005（2010）05-0077-07

2010－06－01

国家高技术研究发展计划重大项目（2006AA06A101）;中国石油大学（华东）自主创新科研计划项目（09CX04058A）

沈跃（1961－），男（汉族），四川大竹人，副教授，博士，从事井下系统、信息与控制工程及智能检测技术的研究。

（编辑 修荣荣）