氢原子钟蓝宝石谐振腔的设计和实验表现

代克，张燕军，王文明，张为群

（1. 中国科学院上海天文台，上海 200030；2. 中国科学院研究生院，北京100039）

氢原子钟蓝宝石谐振腔的设计和实验表现

代克1,2，张燕军1，王文明1,2，张为群1

（1. 中国科学院上海天文台，上海 200030；2. 中国科学院研究生院，北京100039）

为了设计主动型氢原子钟蓝宝石谐振腔的结构尺寸，对根据TE011模式下蓝宝石谐振腔的麦克斯韦尔方程组推出的超越方程进行了求解，利用电磁场有限元分析软件对蓝宝石腔进行了仿真分析。通过计算S参数，确认了所设计的氢原子钟蓝宝石谐振腔实现氢脉泽自激振荡的现实性。利用SOHM-4型氢钟机架作为实验床，在离子泵电流1.1 mA时，得到了强度为-102.93 dbm的脉泽振荡信号。此信号强度与标准的主动型氢原子钟在相同的离子泵电流下的信号强度相仿。

氢钟；蓝宝石谐振腔；有限元分析

随着卫星激光测距（SLR）、甚长基线干涉（VLBI）等空间大地测量技术的发展，氢原子钟作为目前最实用的地面频率标准，已经应用于世界各国地面观测站的建设中。传统的主动型氢原子钟质量大、体积大，许多学者都在氢原子钟小型化方向上进行探索。采用蓝宝石作为填充介质的谐振腔能有效解决氢原子钟小型化的问题，它不仅能减小谐振腔的体积和质量，还能保持接近传统主动型氢原子的频率稳定度。因此，国内外许多研究人员都在从事蓝宝石谐振腔型氢原子钟的研究[1-3]。

1 理论分析和仿真

蓝宝石填充介质谐振腔的结构如图1所示，它由金属外腔和内部蓝宝石填充介质两部分构成。图中a表示金属外腔的半径，b表示内部蓝宝石填充介质外半径，c表示蓝宝石填充介质的内半径，h表示蓝宝石填充介质谐振腔的高度。根据麦克斯韦尔方程组可以推导出蓝宝石填充介质谐振腔在TE011模式下的亥姆霍兹方程，并由此可推导出蓝宝石填充介质谐振腔尺寸与腔频关系的超越方程式（1）[4]，然后可利用matlab6.5软件解此方程来确定TE011模式下蓝宝石腔的尺寸。由于需要蓝宝石腔的光轴与Z轴平行，所以TE011模式下蓝宝石填充介质谐振腔的腔频决定于蓝宝石晶体光轴垂直方向的相对介电常数，其值为9.36，记作rε=9.36。为便于分析，定义1a/ b ρ≡。当设定了外金属腔半径a和高h的值，b可以通过1ρ值来得到，而c可以通过方程式（1）确定，于是可解得蓝宝石填充介质谐振腔的尺寸。

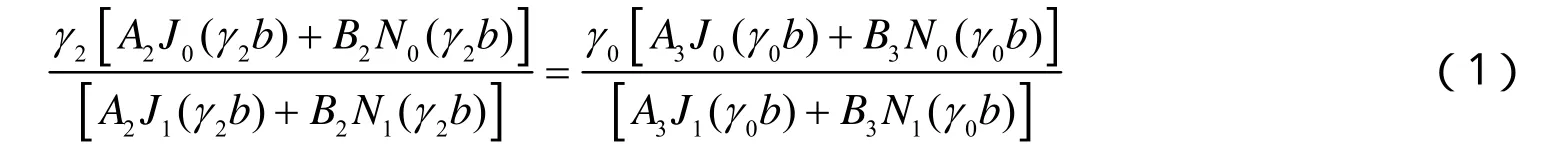
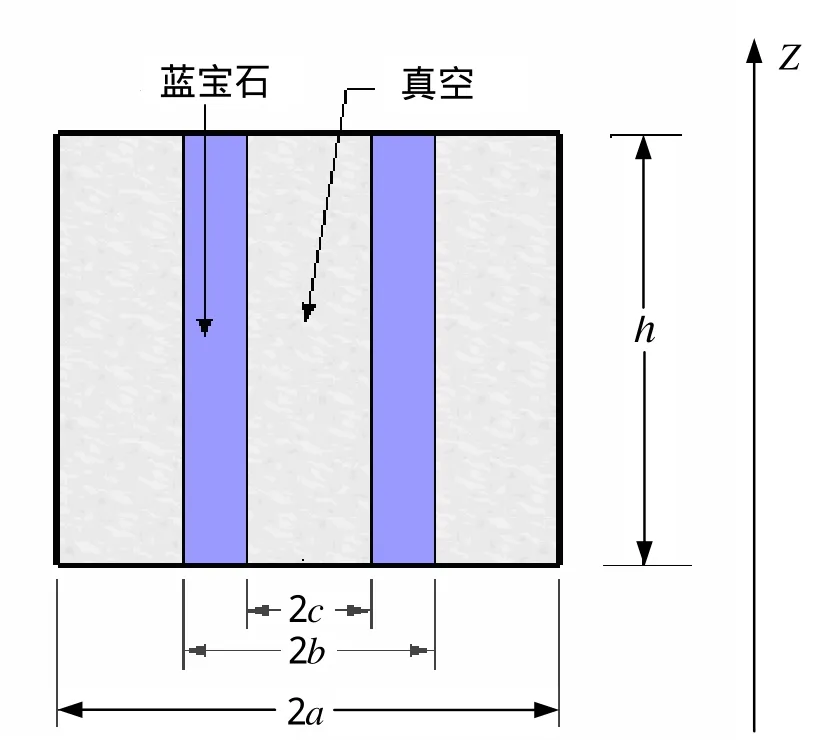
图1 蓝宝石谐振腔结构剖面简图

式（1）中：

式（1）中，ω为蓝宝石腔在TE011模式下的振荡频率，μ0为真空磁导率，ε0为真空介电常数，Jn(X)表示第一类n阶贝塞尔函数，Nn(X)表示第二类n阶贝塞尔函数，εi在蓝宝石区域为εγ，在真空区域为ε。由于腔的体积由a和h来决定，首先设定a=87.5 mm，h=162.9 mm，此时腔的体积为3.92 L，约

0为传统主动型原子钟体积的1/4。在a，h确定的情况下，当ρ1变化时，b和c随其发生变化。计算结果如表1所示。

表1 蓝宝石腔尺寸随1ρ的变化

由于此腔体应用于氢原子钟，我们关心的两个重要参数是有载Q值和填充因子η′，有载Q值反映腔体与外界电路部分耦合以后的损耗，它包括腔体本身的能量损耗和外电路的能量损耗。填充因子η′表征腔内对氢原子超精细跃迁起作用的磁场与整个腔内磁场的比值。有载Q值和填充因子η′的乘积S参数（散射因子）决定腔体是否能够实现氢脉泽自激振荡。由于无载Q值随1ρ增大而减小，在相同外接电路条件下，有载Q值与无载Q值变化成正比关系。而填充因子η′的变化是：当1ρ在0～0.5之间时，η′随1ρ增大而逐渐增大，在1ρ=0.5附近时η′达到最大值，之后逐渐减小。由于填充因子的计算需要仿真分析软件HFSS的场计算器，需要确定尺寸建模完成后才能计算，因此只能通过不同尺寸的仿真结果去接近η′值最大时的1ρ值。1ρ=0.5是我们所作计算的结果中最接近η′最大值的1ρ值，所以这里选择1ρ=0.5时的蓝宝石腔尺寸。

对上面计算得到的蓝宝石腔尺寸（a=87.5 mm，b=43.8 mm，c=36.7 mm，h=162.9 mm），我们利用电磁场有限元分析软件HFSS V10进行了仿真分析。由于软件本身并没有识别TE011模式的能力，我们将腔体内的电场绘制出来（如图2所示）以辨别TE011模式，左边一幅为横截面电场强度分布图，右边一幅为端面电场强度分布图。从端面场形可以看出，根据麦克斯韦方程边界条件横电波端面场强为0，判断其为TE模式，根据横截面电场分布的驻波形式可以看出其模式为TE011。腔体仿真得到的频率为1.435 8 GHz，无载Q值为54 727。

图2 TE011模式下蓝宝石腔横截面和腔端面鉴别场

通过计算式（1）和蓝宝石腔的仿真和实验，我们能得到如表2所示蓝宝石腔的性质。计算蓝宝石腔温度系数的具体方法来源于文献[5]，在此不详述。

表2 腔频率随尺寸及温度的变化

并不是所有的蓝宝石填充介质都能满足脉泽自激振荡，我们可以用S参数判别条件来判断[6]。如果S>5 900，那么谐振腔便可以实现氢脉泽自激振荡。经网络分析仪测试腔体的有载Q值约为45 000，如图3所示。腔体的填充因子η′可以利用式（2）[7]通过仿真软件计算得到，其值为0.523，由此可算得S=23 535，该值大于5 900。这样我们就从理论上证实了此腔体可以实现氢脉泽自激振荡。

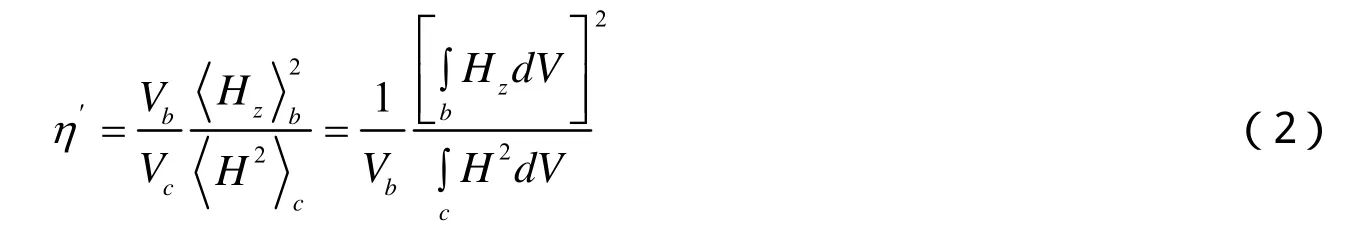
式（2）中，Vb为储存泡体积，Vc为谐振腔体积，H为总体场强度，Hz为Z向磁场强度。

图3 蓝宝石腔的腔频和有载Q值

2 蓝宝石谐振腔实验

为了验证蓝宝石填充介质谐振腔能够在实验上实现氢脉泽自激振荡，我们对腔体进行了脉泽振荡实验。我们利用传统的主动型原子钟（SOHM-4）作为试验床，利用它的真空系统和电子系统，这是一种节省成本的方法。用一个设计好的架子将蓝宝石谐振腔固定于SOHM-4的真空系统内，经过C场、氢分子电离效果及氢流量的调试，当离子泵电流为1.1～1.2 mA时（离子泵真空本底电流为0.3 mA），我们得到了强度为-102.9 dbm的脉泽振荡信号，如图4所示。

通过脉泽信号稳定度测试，我们得到1 s稳定度为9.8×10-13，10 s稳定度1.33×10-13。由于固定蓝宝石谐振腔的架子存在应力问题，且SOHM-4型标准主动型原子钟温度控制系统的温控精度不能满足高温度系数的蓝宝石谐振腔的要求，我们得到的长期稳定度结果很差。

图4 蓝宝石谐振腔氢钟的自激振荡信号

3 结语

我们设计了用于替代标准主动型氢原子钟谐振腔的小型蓝宝石填充介质谐振腔，从理论和实验两方面验证了它能够实现氢脉泽自激振荡。下一步工作是围绕腔体的物理部分的小型化设计工作，包括蓝宝石腔型氢原子钟束光学系统的设计，磁屏蔽系统的设计，精密温控系统的设计等等。由于蓝宝石谐振腔本身的温度系数很高，精密温度控制和电子自动调谐系统都是保证蓝宝石主动型氢原子钟中期和长期稳定性的必要条件，这些都是我们未来研究中必须解决的问题。

[1] MORIKAWA T, TAKAHEI K, UEHARA M, et al. Design Optimization of a Sapphire Loaded Cavity for a Spaceborne Hydrogen Maser[C] // Proceeding of 14th EFTF, 2000: 462-465.

[2] 王暖让, 周铁中, 高连山. 氢频标蓝宝石微波腔的小型化进展[C] // 2008全国频率控制技术年会论文集. 北京: 2008全国频率控制技术年会组委会, 2008: 144-147.

[3] ZIVANOV S, SCHWEDA H, GOUJON D, et al. Physics Package of the 35 kg Active Hydrogen Maser for the ACES Space Mission of ESA Frequency Control Symposium[C] // 2007 Joint with the 21st European Frequency and Time Forum. IEEE International, 2007, 10(1): 637-641.

[4] 曹昱, 吕善伟, 冯克明. 氢频标部分充填介质微波腔模式分裂的分析[J]. 系统工程与电子技术, 2005, 27(7): 1199-1202.

[5] CAO Yu. Frequency-temperature Analysis of Sapphire Ring Dielectric-loaded Cylindrical Cavity in Hydrogen Maser Atomic Frequency Standard[C] // 2004 Asia-pacific Radio Science Conference, 2005, 4: 13-16.

[6] 王庆华, 翟造成, 张为群, 等. 小型TE111无泡隔膜腔氢脉泽的实验研究[J]. 计量学报, 2000, 21(2): 89-94.

[7] VANIER J, AUDION C. The Quantum Physics of Atomic Frequency Standards[M]. Bristol and Philadelphia: Adam Hilger, 1989.

A Design of Sapphire Loaded Cavity for H-maser and Its Experimental Performance

DAI Ke1,2, ZHANG Yan-jun1, WANG Wen-ming1,2, ZHANG Wei-qun1

(1. Shanghai Astronomical Observatory, Chinese Academy of Sciences, Shanghai 200030, China;
2. Graduate University of Chinese Academy of Sciences, Beijing 100039, China)

To design the dimensions of sapphire loaded cavity for active H maser, we solved the transcendental equation which was deduced from Maxwell equations for the cavity in TE011 mode. By FEM (finite element methods) simulation of the cavity, the solution we got was confirmed. Then the ability of the cavity to sustain self-oscillation was calculated. With the active H maser SOHM-4 as a experimental bed, an H maser signal with oscillation power of -102.93 dBm was obtained from the sapphire loaded cavity, while the ion pump flux was about 1.1 mA. The signal power is almost as same as that of the standard active H maser, for the same ion pump flux.

H-maser; Sapphire loaded cavity; FEM (finite element methods) simulation

TM935.115

A

1674-0637(2010)02-0103-05

2009-11-30

上海市自然科学基金资助项目（10ZR1435900）

代克，男，硕士，主要从事蓝宝石型氢原子钟方面的研究。