三能级Tonks-Girardeau气体的Ramsey干涉的研究

刘先锋，韩玖荣，张首刚

（1. 扬州大学物理科学与技术学院，扬州 225002；

2. 中国科学院国家授时中心，西安 710600；

3. 中国科学院时间频率基准重点实验室，西安 710600）

三能级Tonks-Girardeau气体的Ramsey干涉的研究

刘先锋1，韩玖荣1，张首刚2,3

（1. 扬州大学物理科学与技术学院，扬州 225002；

2. 中国科学院国家授时中心，西安 710600；

3. 中国科学院时间频率基准重点实验室，西安 710600）

采用Ramsey分离振荡场方法，研究了紧束缚一维强相互作用的超冷玻色气体在Tonks-Girardeau区的Ramsey干涉。在等失谐情况下，干涉条纹宽度随着原子与分离场作用时间和拉比（Rabi）频率的增大而变窄。对量子投影噪声的研究表明，相比二能级Tonks-Girardeau气体，对于三能级模型，通过控制原子总数和调节外场可以降低量子噪声, 有效地减少噪声对Tonks-Girardeau气体系统的干扰。原子干涉的探索对提高量子频率标准的精度具有重要理论指导意义。

Tonks-Girardeau气体；Ramsey干涉；量子投影噪声

在量子多体系统中强关联问题已经引起人们广泛的关注，而Tonks-Girardeau（TG）气体[1]就是其中之一。TG气体是以物理学家Tonks和Girardeau名字命名的，描述了由类似费米子性质的具有强相互作用的玻色子构成的一维系统。然而，这样的玻色子的量子行为并不完全等同于理想的费米子，它们的特征动量分布就反映了这一点。最近，2个实验[2-3]首次利用光晶格实现了TG区域并且观察到了TG气体的性质，从而引起了在量子信息、量子计算、量子相干和强关联系统等方面的研究。原子囚禁和冷却技术的发展促进了实验上成功地制备了低维气体[4-5]。利用费米-玻色映射（Fermi-Bose mapping）方法[1,6]，可将无相互作用无自旋的费米子波函数映射到硬核玻色子，因此TG模型是完全可解的。近期，Girardeau的费米-玻色映射方法已被用来研究TG气体[7-8]、TG混合原子气体[9]以及二能级原子系统[10-11]。

Ramsey干涉技术在现代精密测量、量子频标等方面有着重要运用，据此提出和实现了多种观察原子干涉的实验方案。相干布居囚禁（CPT）方法便是上述实验方案之一[12]，先后有多个研究小组运用此方法得到了碱金属原子束[13-14]和蒸汽原子[15-16]的干涉图样[17]；此外，基于早年Ramsey提出的空间分离振荡场方法[18-19]，Muga领导的研究小组分别运用半经典和全量子的处理方法对二能级铯原子干涉进行了研究[10-11,20-21]。

根据Ramsey的观点，原子通过空间两个外场的间隔区域的时间越长，所得到的中央干涉条纹就越窄[18-19]，基于这一点，超冷原子被广泛运用。原子囚禁和冷却技术的发展为实验上制备低维原子气体进入TG区提供了有力的技术支持。一方面，近几年来，研究者们先后提出了利用光晶格(OL)、磁光晶格（MOL）、谐振子势阱、雪茄型势阱等的原子囚禁方案[2-3,22-28]；另一方面，运用激光冷却或蒸发冷却可以将原子冷却到接近0 K的温度。在Ramsey干涉条纹研究过程中，诸多其他因素值得考虑，量子运动效应就是其中之一。无论是纵向的还是横向的运动都会破坏Ramsey条纹[18-19,29]。最近，Seidel和Muga在量子运动效应对原子干涉影响方面的研究表明[26-28]，由于受到量子反射和隧穿的影响，干涉条纹发生了改变。为了利用原子干涉，寻找更高精度的原子钟，有研究者提出可以运用玻色-爱因斯坦凝聚（BEC），因为借此可利用它的低速度和窄速率分布特性，但是玻色-爱因斯坦凝聚中碰撞频移和不稳定性的存在[30]将会对原子频标的精度产生影响。近年来对TG气体的研究结果，引起了我们对TG气体的关注并试图对其Ramsey干涉进行研究。在足够低密度和强相互作用下限制原子的横向运动，玻色气体进入TG区域。与一般原子气体相比，TG气体具有一维性和狭窄的速率分布优势；此外，TG气体很好地抑制了三体关联作用[31]，从而增强了TG气体的稳定性。另外，TG气体成功克服了玻色-爱因斯坦凝聚中出现的碰撞频移和不稳定等问题。

运用Ramsey方法[18-19]研究原子干涉，寻求更高精度的原子钟已成为现代精密测量方面的有力工具。近期，TG气体的二能级原子Ramsey干涉已被报道[10-11,20-21]，然而二能级原子的运用并不是最佳的，相比之下，三能级TG气体更具优势，更具应用前途。本文将研究三能级TG气体的Ramsey干涉及量子投影噪声。

1 三能级TG气体的Ramsey干涉

1.1 理论模型

我们把超冷玻色气体装载到雪茄型谐振子势阱中，当横向角频率ω⊥远大于纵向的角频率ωz，从而在横方向能级之间的能量差非常大，因此被囚禁的原子在这个方向上跃迁要比纵向上跃迁困难得多。原子只能在横向基态作零点振动，此时系统的横向自由度被冻结了，原子可以在纵向运动，于是原子气体呈现出准一维特性。现利用雪茄型谐振子势阱对N个三能级超冷玻色原子进行囚禁，在很强的径向束缚势下，使玻色气体进入TG区域。如图1所示，所有超冷玻色原子在初始t0时刻都制备在基态，它们具有一个小动量ħk0，在t0到t0+τ和t0+T+τ到t0+T+2τ这两段时间内施加两个完全一样的振荡电磁场。每一个振荡场由两种频率的激光场构成，TG原子气体的电子则由基态|g＞到激发态|a＞和|b＞，即发生跃迁。

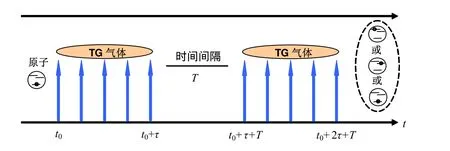
图1 Ramsey干涉示意图

对于V型三能级超冷玻色原子，包含三个量子态：基态|g＞，激发态|a＞和|b＞，对应的能量分别是Eg=ħωg，Ea=ħωa和Eb=ħωb，如图2所示。在频率分别为v1和v2的外加激光场的作用下，原子和激光场相互作用。设外场频率和原子跃迁频率的失谐Δa=v1−(ωa−ωg)和Δb=v2−(ωb−ωg)。其中，|a＞↔|g＞和|b＞↔|g＞的跃迁是偶极允许的，而|a＞↔|b＞跃迁偶极禁戒。

在偶极旋波近似下，相互作用绘景中，对于单个原子，系统的哈密顿量表示为[32]

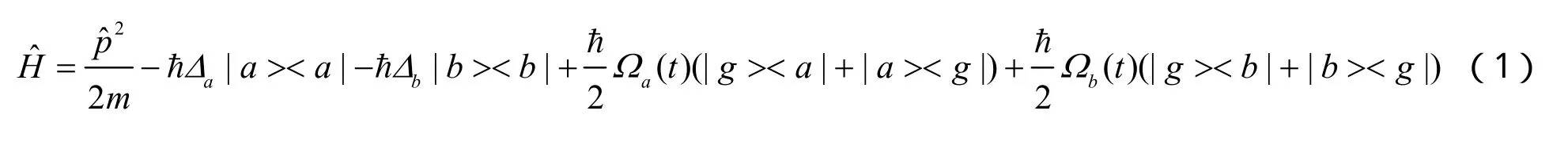
式（1）中，第一项表示原子的动能，Ωj(t)（其中j=a，b）表示两外场的拉比（Rabi）频率，是时间的函数。

1.2 薛定谔方程的半经典解

对原子的质心运动可以进行经典处理，并且与系统的内部状态无关[21,33]，因此，在半经典处理情况下，相互作用绘景中的波函数|ψI(t)＞是以下薛定谔方程的解

初始时刻，原子处于基态|ψI(t0)＞=|g ＞，在时域t∈[t0, t0+τ]内原子与外场相互作用时间τ后，接着原子在T时间内停止与外场作用，这一过程中相互作用绘景中哈密顿量为零，因此演化算符为单位矩阵。最后，原子在时域t∈[t0+T+τ, t0+T+2τ]内与外场作用时间τ。原子末态可表示为

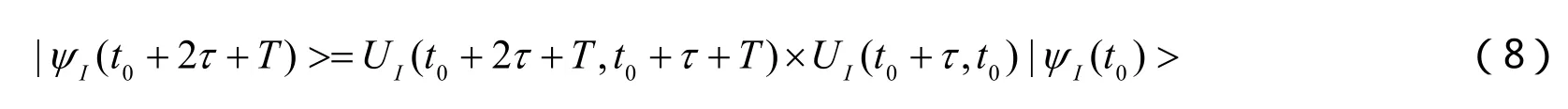
1.3 讨论

Ramsey干涉条纹指的是与外场相互作用后，原子处于激发态的几率和外场频率与原子跃迁频率间失谐量的关系。利用式（8），可计算得到原子处于激发态总的几率为

由式（9）至式（12）可知，对于三能级的TG气体原子来说，Ramsey干涉条纹由失谐Δ，拉比频率以及场作用时间τ决定。在图3中，我们分别画出了Ωa=Ωb和Ωa≠Ωb这两种情况下Ramsey的干涉条纹P(Δ)。很明显，干涉图样关于Δ=0对称分布。

图3 等拉比频率（Ωa=Ωb =π/2）与非等拉比频率（Ωa=π，Ωb=π/2）下的Ramsey干涉条纹P(Δ)（其他参数：T＝10 s，τ=1 s）

接下来，我们计算了Ramsey干涉随原子和场的作用时间τ的变化关系，选择参数如下：T=5 s，以及==π/2，在图4中分别给出了等失谐情况下当τ =1 s和τ =5 s时的干涉。可见，随着原子和场作用时间的增加，干涉图样更加狭窄，另外P(Δ)的最大值增大。对于拉比频率不相等的情况，我们同样得到了与上述一致的结论。

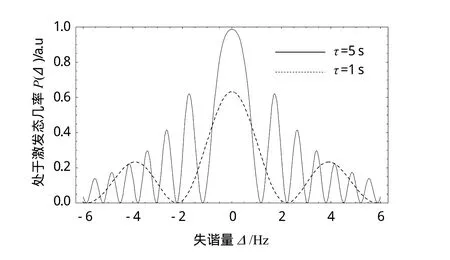
图4 当场和原子作用时间τ =1 s和τ =5 s时Ramsey干涉条纹（拉比频率取为==π/2）

为研究激发态原子概率P()Δ随失谐Δ和拉比频率aΩ，bΩ以及原子和外场作用时间τ三者的变化关系，利用式（11）和式（12）得到

图5 P(Δ)与 /rad的关系图

图5给出了处于激发态概率P(Δ)与Ωτ'的关系图，其中q=Δ2/(+)。图5表明，随着q值的增大，P(Δ)的最大值减小。若q→0，即+＞＞Δ2，则P(Δ)→1；若q→+∞，即+＜＜Δ2，则P(Δ)→0。

2 三能级TG气体的量子投影噪声

我们已经讨论了TG区单个原子的情况，然而对于Ramsey干涉，处于激发态原子的数目涨落问题是不能忽视的，接下来我们将计算三能级TG气体的量子投影噪声并且与二能级系统进行比较。

考虑到系统已由二能级系统转为三能级系统，为了能准确表述三能级系统量子投影噪声，在此首先引入单跃迁算符[34]，可具体表示为

这里r和s代表原子三个能级g，a和b，但是r和s不能同时分别为a和b，而x，y，z表示单跃迁算符可进行投影的3个不同方向。利用以上结论可以得到

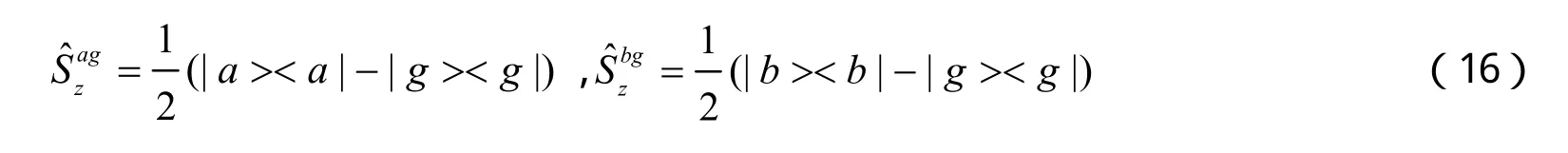
量子噪声实则反映了对于N粒子组成的系统处于激发态原子数目的涨落。在此，我们应用波函数ΨB(x1,...,xN)计算量子噪声。对于一个处于基态的三能级超冷玻色原子系统，通过与外场相互作用发生了|a＞↔|g＞和|b＞↔|g＞的2种可能的跃迁。接下来，我们计算这2种中任何一种情况的量子投影噪声情况。考虑由N个原子构成的系统，有n个原子发生了|g＞→|a＞跃迁（n≤N），剩余的N-n个原子发生了|g＞→|b＞跃迁，根据文献[35]，对于三能级系统，投影算符表示为

为了计算期待值，实际计算过程中可利用玻色-费米映射（Bose-Fermi mapping），即ΨB(x1,...,xN)=ΑΨF(x1,...,xN)，其中反对称单位函数Α=sgn(xk−xj)，我们可以用费米子波函数ΨF代替玻色子波函数ΨB。

式（19）中Φi和Φj分别表示第i个和第j个粒子的波函数，αi=＜Φi|ai＞＜ai|−|gi＞＜gi|Φi＞和βj=＜Φi|bj＞＜bj|−|gj＞＜gj|Φi＞表示两种跃迁下粒子处于激发态与基态概率之差。通过进一步推导得

三能级与二能级相比，量子投影噪声差值为

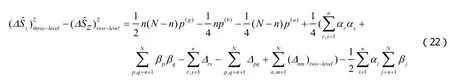
式（22）描述了三能级系统与二能级系统TG气体的量子投影噪声的差值，这与粒子数N，量子投影算符的期待值，以及α和β值有关。显然，如果我们实验上控制基态和两个激发态之间的耦合场的强度或者失谐的大小，那么我们可使得式（22）为负值，也就是说三能级系统相比于二能级系统量子噪声变得更小。通过调节外场减小量子噪声，起到了对强相互作用TG气体的负的修正作用。因此，抑制噪声是我们目前的这个系统的一个突出优点。另外，与二能级原子系统相比，三能级超冷玻色原子系统可以对两个场进行调节、控制，实验控制手段更为丰富。

3 结论

本文对三能级超冷TG气体的Ramsey干涉和量子投影噪声进行了研究。发现一维强相互作用的玻色气体在实现了TG气体的情况下具有窄的速率分布，用以研究Ramsey干涉具备较长的相干时间，TG强相互作用玻色气体表现出类似于费米子的性质，两者的数密度等同，在TG气体中，可以避免玻色-爱因斯坦凝聚中出现的碰撞频移和不稳定性等问题。研究表明，等失谐情况下，三能级Ramsey干涉条纹宽度随着与场相互作用时间和拉比频率的增大而变小。量子投影噪声的计算结果显示，通过控制原子数目和对外场的调节，能够使量子噪声比二能级系统中更小。三能级TG气体在抑制量子噪声方面有显著作用，此外，三能级系统提供了更为丰富的实验控制手段。

对三能级TG理想气体干涉的理论研究，对原子频标的研究、提高原子频标的精度具有很好的理论指导作用，可望在不久的将来TG气体在原子干涉方面能有更广泛的用途。

[1] GIRARDEAU M. Relationship Between Systems of Impenetrable Bosons and Fermions in One Dimension[J]. Journal of Mathematical Physics, 1960, 1(6): 516-523.

[2] PAREDES B, WIDERA A, MURG V, et al. Tonks-Girardeau Gas of Ultracold Atoms in an Optical Lattice[J]. Nature, 2004, 429(6989): 277-281.

[3] KINOSHITA T, WENGER T, WEISS D S. Observation of a One-dimensional Tonks-girardeau Gas[J]. Science, 2004, 305(5687): 1125-1128.

[4] OLSHANII M. Atomic Scattering in the Presence of an External Confinement and a Gas of Impenetrable Bosons[J]. Physics Review Letters, 1998, 81(5): 938-941;

[5] BERGEMAN T, MOORE M G, OLSHANII M. Atom-atom Scattering Under Cylindrical Harmonic Confinement: Numerical and Analytic Studies of the Confinement Induced Resonance[J]. Physics Review Letters, 2003, 91(16): 163201.1-163201.4.

[6] GIRARDEAU M D, WRIGHT E M. Dark Solitons in a One-dimensional Condensate of Hard Core Bosons[J]. Physics Review Letters, 2000, 84(25): 5691-5694.

[7] MINGUZZI A, GIRARDEAU M D. Pairing of a Harmonically Trapped Fermionic Tonks-Girardeau Gas[J]. Physics Review A, 2006, 73(6): 063614.1-063614.4.

[8] BENDER S A, ERKER K D, GRANGER B E. Exponentially Decaying Correlations in a Gas of Strongly Interacting Spin-polarized 1D Fermions with Zero-range Interactions[J]. Physics Review Letters, 2005, 95(23): 230404.1-230404.4.

[9] GIRARDEAU M D, MINGUZZI A. Soluble Models of Strongly Interacting Ultracold Gas Mixtures in Tight Waveguides[J]. Physics Review Letters, 2007, 99(23): 230402.0-230402.4.

[10] MOUSAVI S V, CAMPO A, LIZUAIN I, et al. Seeking Better Times: Atomic Clocks in the Generalized Tonks-Girardeau Regime[J]. Journal of Physics: Conference Series, 2008, 99: 012014.0-012014.8.

[11] MOUSAVI S V, CAMPO A, LIZUAIN I, et al. Ramsey Interferometry with a Two-level Generalized Tonks-Girardeau Gas[J]. Physics Review A, 2007, 76(3): 033607.1-033607.9.

[12] ARIMONDO E. Coherent Population Trapping in Laser Spectroscopy [J]. Progress in Optics, 1996, 35: 257.

[13] THOMAS J E, HEMMER P R, EZEKIEL S, et al. Observation of Ramsey Fringes Using a Stimulated, Resonance Raman Transition in a Sodium Atomic Beam[J]. Physics Review Letters, 1982, 48(13): 867-870.

[14] HEMMER P R, SHAHRIAR M S, RIVERA H L, et al. Semiconductor Laser Excitation of Ramsey Fringes by Using a Raman Transition in a Cesium Atomic Beam[J]. Journal of the Optical Society of America B, 1993, 10(18): 1326-1329.

[15] ZIBROV A S, MATSKO A B. Optical Ramsey Fringes Induced by Zeeman Coherence[J]. Physics Review A, 2001, 65(1): 013814.1-013814.10.

[16] ZANON T, GUERANDEL S, CLERCQ E D, et al. High Contrast Ramsey Fringes with Coherent-population-trapping Pulses in a Double Lambda Atomic System[J]. Physics Review Letters, 2005, 94(19): 193002.1-193002.4.

[17] BUDKER D, GAWLIK W, KIMBALL D F, et al. Resonant Nonlinear Magneto-optical Effects in Atoms[J]. Review of Modern Physics, 2002, 74(41): 1153-1201.

[18] RAMSEY N F. A Molecular Beam Resonance Method with Separated Oscillating Fields[J]. Physics Review, 1950, 78(6):695-699.

[19] RAMSEY N F. Experiments with Separated Oscillatory Fields and Hydrogen Masers[J]. Review of Modern Physics, 1990, 62(3): 541-552.

[20] SEIDEL D, MUGA J G. Ramsey Interferometry with Guided Ultracold Atoms[J]. European Physics Journal D-Atomic, 2007, 41(1): 71-75.

[21] SEIDEL D, MUGA J G. Two-frequency Ramsey Interferometry[J]. Physics Review A, 2007, 75(2): 023811.1-023811.7.

[22] HAN Jiu-rong, LIU Jin-ming, JING Hui, et al. Energy Spectrum of Two-component Bose-einstein Condensates in Optical Lattices[J]. Communications in Theoretical Physics, 2005, 43(5): 809-813.

[23] XU Guang-yuan, YAN Li, WANG Yang-jun, et al. Study of Dynamical Behaviour and Fermionization of a Bosonic Gas in Funnel Potential[J]. Chinese Physics B, 2008, 17(11): 4158-4162.

[24] DUNJKO V, LORENT V, OLSHANII M. Bosons in Cigar-shaped Traps: Thomas-fermi Regime, Tonks-girardeau Regime, and in Between[J]. Physics Review Letters, 2001, 86(24): 5413-5416.

[25] PEDRI P, SANTOS L. Three-dimensional Quasi-tonks Gas in a Harmonic Trap[J]. Physics Review Letters, 2003, 91(1): 110401.1-110401.4.

[26] LIANG Zhao-xing, ZHANG Zheng-dong, LIU Wei-min. Dynamics of a Bright Soliton in Bose-Einstein Condensates with Time-dependent Atomic Scattering Length in an Expulsive Parabolic Potential[J]. Physics Review Letters, 2005, 94(5): 050402.1-050402.4.

[27] LIU Wei-min, FAN Wen-bin, ZHENG Wei-mou, et al. Quantum Tunneling of Bose-einstein Condensates in Optical Lattices Under Gravity[J]. Physics Review Letters, 2002, 88: 170408.1-170408.4.

[28] JI An-chun, SUN Qing, XIE Xin-cheng, et al. Josephson Effect for Photons in Two Weakly Linked Microcavities[J]. Physics Review Letters, 2009, 102(2): 023602.1-023602.4.

[29] SEIDEL D, MUGA J G. Quantum Motion Effects in Atom Interferometry[J]. Israel Journal of Chemistry, 2007, 47(1): 67-73.

[30] KADIO D, BAND Y B. Analysis of a Magnetically Trapped Atom Clock[J]. Physics Review A, 2006, 74(5): 053609.1-053609.10.

[31] GANGARDT D M, SHLYAPNIKOV G V. Stability and Phase Coherence of Trapped 1D Bose Gases[J]. Physics Review Letters, 2003, 90(1): 010401.1-010401.4

[32] SCULLY M O, ZUBAIRY M S. Quantum Optics[M]. Cambridge University Press, 2003.

[33] DAMBORENEA J A, EGUSQUIZA I L, HEGERFELDT G C, et al. On Atomic Time-of-arrival Measurements with a Laser of Finite Beam Width[J]. Journal of Physics B, 2003, 36(12): 2657-2669.

[34] WOKAUN A, ERNST R R. Selective Excitation and Detection in Multilevel Spin Systems: Application of Single Transition Operators[J]. Journal of Chemical Physics, 1977, 67(4): 1752-1758.

[35] ITANO W M, BERGQUIST J C, BOLLINGER J J, et al. Quantum Projection Noise: Population Fluctuations in Two-level Systems[J]. Physics Review A, 1993, 47(5): 3554-3570.

Study of Ramsey Interferometry with Three-level Tonks-Girardeau Gas

LIU Xian-feng1, HAN Jiu-rong1, ZHANG Shou-gang2,3

(1. College of Physics Science and Technology, Yangzhou University, Yangzhou 225002, China;
2. National Time Service Center, Chinese Academy of Sciences, Xi’an 710600, China;
3. Key Laboratory of Time and Frequency Primary Standards, Chinese Academy of Sciences, Xi’an 710600, China)

The Ramsey’s method of separated oscillatory fields is applied to study Ramsey interferometry but using a Tonks-Girardeau model that describes a coherent one-dimensional gas of ultracold bosons with strong interactions. Under the equal detuning, the interference fringes width can be narrowed by increasing the Rabi frequency and the field-crossing time. Moreover, we gain further insight into the quantum projection noise. In contrast to a two-level TG gas, our results illustrate that the modulation of the total number of three-level atoms and the external fields tend to lower the quantum noise limit, so as to reduce the interference of the noise to the strongly interacting bosonic Tonks-Girardeau gas. The investigation on the atomic interferometry is a great theoretical guidance to the research of quantum frequency standard.

Tonks-Girardeau gas; Ramsey interferometry; quantum projection noise

TM935.113

A

1674-0637(2010)02-0081-11

2009-12-22

国家自然科学基金重点资助项目（10834007）；中国科学院重要方向资助项目（KJCX2-SW-T12)；国家自然科学基金专项类资助项目（10647144）；扬州大学自然科学基金资助项目（GK0513102）

刘先锋，男，硕士研究生，主要从事凝聚态物理方面的研究。