灰色系统理论在我国就业人数预测中的应用

罗明奇,王利红,马少仙

(1.西北民族大学 计算机科学与信息工程学院,甘肃 兰州 730030;2.兰州交通大学 数理与软件工程学院,甘肃 兰州 730070)

灰色系统理论在我国就业人数预测中的应用

罗明奇1,王利红2,马少仙1

(1.西北民族大学 计算机科学与信息工程学院,甘肃 兰州 730030;2.兰州交通大学 数理与软件工程学院,甘肃 兰州 730070)

以我国1999—2006年的就业人数数据为依据,利用灰色系统理论原理,对我国就业人数的原始数据进行弱化处理,以减少冲击波对数据的影响。对弱化后的数据序列处理中引入多元统计思想,确定最终弱化的终止条件,然后以此弱化后的数据为基础建立灰色 GM(1,1)微分模型-x(1)=38 164.384 6。根据灰色系统理论原理得知模型不具有很好的预测效果。探究了模型失效的缘由,提出了模型改进的建议。

灰色系统理论;弱化算子;就业人数;预测

我国高等教育规模的逐步扩大,高校的持续扩招,使得这几年的高校毕业生人数逐步增加,在就业方面的压力已经显现,大学生充分就业已经是一个问题。我国经济的持续高速发展,经济结构的逐步调整,使得劳动力需求也逐步增加。社会的进步,城镇化建设的进一步深化,使得越来越多的农村剩余劳动力脱离农村进入城市。由于农村人口占我国人口的大多数,这就隐性增加了就业人数,给社会形成了极大的就业压力。但是,我们也注意到,当我国经济快速增长的时候,相应的失业率也在增长,奥肯定律在我国失效了。失效的原因:一方面是由于随着社会的进步,科学技术的发展使得越来越多的智能机器设备取代了人力;另一方面,随着我国计划生育法的观念进一步深入,优生优育的观念已经被社会接受,我国的人口增长率在逐渐放缓。

但是我国所面临的就业压力还是巨大的,本文以我国1999—2006年的就业人数数据为依据,引入弱化算子的作用,减少冲击波对数据的影响,建立灰色 GM(1,1)微分模型,并对我国以后各年的就业人数进行预测分析,以期对以后各年的就业安排有所帮助。

一、相关理论

从1982年邓聚龙教授创立灰色系统理论(Gray Theory)以来,灰色系统理论已经广泛应用于各个学科中。艾什比(Ashby)将内部信息未知的对象称为黑箱(Black Box),这种称谓已被人们普遍接受。灰色系统理论的基本思想是:根据序列曲线几何形状的相似程度判断其关联程度,曲线越接近,序列之间的关联程度越大,反之关联程度越小。即根据系统行为特征数据和相关因素数据即可做出各个序列的图形,从直观上就可以判定,进行系统分析。选准系统行为特征的映射量之后,还需要进一步明确影响系统主行为的有效因素。如要作量化研究分析,则需要对系统行为特征映射和各个有效因素进行适当处理,通过算子作用,使之化为数量级大体相近的无量纲数据,并将负相关因素转化为正相关因素[1-3]。

定理1[4]设原始数据序列是

二、模型的构造和预测

选取我国1999—2006年的就业人数数据,如表1(本文所有数据均来源于文献[5])

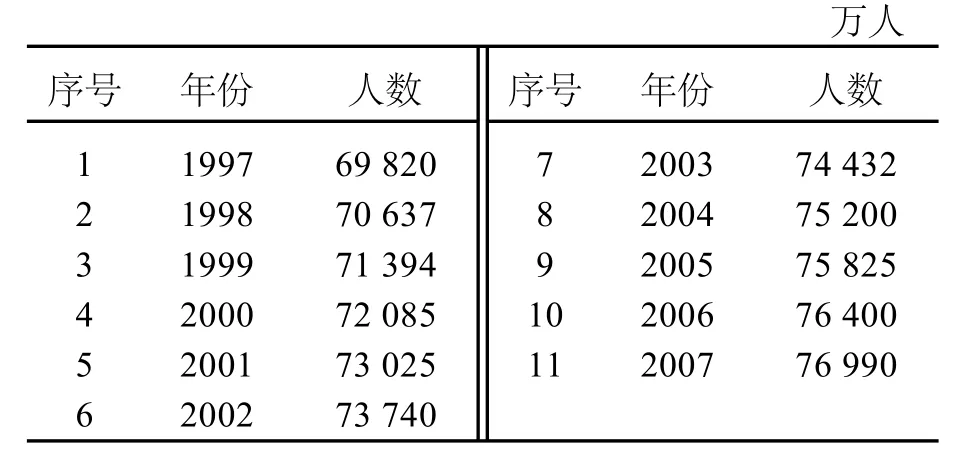
表1 1997—2007年我国就业人数情况表

对表1的1999—2006年的数据进行弱化处理,2007年的数据作为对比参照,以说明弱化的程度,只要使得弱化达到一定的精度即可,如定理1引入弱化算子,处理后的数据见表2。

分别依据二阶弱化和三阶弱化后的数据建立回归方程,得:

其中,式(1)为按照二阶弱化后的数据建立的模型,式(2)为按照三阶弱化后的数据建立的模型,它们的拟合优度分别为=0.998 6=0.999 1。说明对原始数据进行弱化处理之后建立的回归模型很好地拟合了数据。经检验,给定α=0.05时方程(1)、(2)显著。据此进行预测,即在方程(1)、(2)中带入x=11,分别得到:y2=76 600.9,y3=76 492.46。

表2 经弱化算子作用之后的数据表 万人

与作为对比的2007年的数据相对照,对原始数据二阶弱化即可。

当k＞4时,序列X(0)的准光滑性条件满足,X(1)准指数规律满足,由此选取2003—2007年的数据序列为基础建立灰色GM(1,1)微分模型。

在灰色系统理论中a为发展系数,b为灰色作用量,-a反映了^x-1与^x(0)的发展态势。一般情况下,系统作用量应是外生的或者是前定的,而 GM(1,1)微分模型是单序列序建模,只用到系统的行为序列,而无外作用序列。GM(1,1)微分模型中的灰色作用量b是从背景值中挖掘出来的数据,它反映数据变化的关系,其确切内涵是灰色的,灰色作用量是内涵外延化的具体体现。虽然在本例中引入了弱化算子的作用,减少了冲击波对数据的干扰,使得数据尽可能的在相同的平台上,但是这种引入致使所得到的经过二阶算子作用的数据序列并不适用于 GM(1,1)微分模型建模。

三、展 望

虽然在本文中按照多元统计的思想,在对原始数据序列进行弱化处理中,成功达到了确定弱化算子阶数的目的。但是最后经过二阶弱化算子作用的序列建立了灰色 GM(1,1)微分模型-x(1)=38 164.384 6。经过分析研究发现该模型并没有达到精确预测的功能,其预测价值不大,需要对模型进行改进。因有灰色系统理论的知识,当发展系数a=-1时,适宜使用灰色残差修正GM(1,1)微分模型。同时由于数据本身的缘由会产生误差,在计算的过程中由于数据的精度问题也会产生误差,而且在处理数据时并没有完全体现新信息优先原理,本文对此提出两点改进方案:

(1)对信息进行加权处理。对新信息进行加权处理,新信息的权重大于老信息的权重,体现新信息优先原理。

(2)反序建模。前述的GM模型都是以序列X(1)的第一个分量作为灰色模型的初始条件,这样对新信息利用不够充分,往往会影响预测的精度,若以X(1)的任意一个分量作为灰色模型的初始条件,选择误差最小为初值,预测精度将会极大的提高。

[1] 安宁,罗珊.广东省科技投入与经济增长关联的实证分析[J].科技管理研究,2008(12):190-192.

[2] 屈小娥,袁晓玲.中国能源消费与经济增长的灰色关联分析[J].统计与决策,2008(14):86-88.

[3] 李建伟,荣良骥.甘肃省科技经费投入与经济增长的灰色关联度分析[J].甘肃科技,2008(13):13-15.

[4] 刘思峰,党耀国,方志耕,等.灰色系统理论及其应用[M].北京:科学出版社,2005:29-31.

[5] 中华人民共和国国家统计局.中国统计年鉴2008[M].北京:中国统计出版社,2009.

L UO Mingqi1,WAN G Lihong2,MA Shaoxian1

(1.Computer Science and Information Engineering College,Northwest University for Nationalities,Lanzhou 730030,China;2.School of Mathematics,Physics and Software Engineering,Lanzhou Jiaotong University,Lanzhou 730070,China)

Applied Research in Forecast Employment Population with Grey System Theory

Taking the employment population data of 1999-2006 of China as the basis,using the principle of grey system theory,the employment population’s primary data is weaken down,in order to reduce the influence of the shock-wave to the data.The multivariate statistical processing is introduced to the weakened data sequence,and the termination conditions of the final weakening are determined,then the gray GM(1,1)differential model-x(1)=38 164.384 6,the is established.According to the grey system theory,the model does not have a good prediction.The reasons for failure of the model are explored;recommendations for improving the model are put forward.

grey theory;weakening operator;employment volume;forecast

O 29

A

1008-9225(2010)03-0108-03

2010-03-04

罗明奇(1985-),男,甘肃天水人,西北民族大学硕士研究生。

【责任编辑 刘晓鸥】