船体曲面矩形块按参考线敷设法关键技术研究

吴年庆， 赵 耀， 袁 华

（华中科技大学，湖北 武汉 430074）

船体曲面在敷设矩形块时，要进行布置设计，以便达到外观整齐、减少矩形块总体消耗量等目的。目前采用的方法是，将船体外表面按肋骨线方向进行单向展开，在展开图上进行矩形块的模拟布置，并输出敷设信息。由于在肋骨线方向单向展开存在着较大误差，使得最终布置设计结果与实船敷设结果差异较大，无法达到在水线面上整齐、美观、连续等敷设效果；同时，由于是手工模拟敷设，形成单一全船草方案费时费力，达3 人3 月以上。因此，本研究提出在船体曲表面计算机三维模型上实施的矩形块按参考线敷设法，以指导实船敷设[1]。

矩形块按参考线敷设法就是首先在船体曲面计算机三维模型上生成矩形块敷设参考线，然后以生成的敷设参考线为基准进行矩形块的布置设计，以达到布置的矩形块整齐、美观、连续等敷设效果和满足工程使用要求，指导实船矩形块的敷设。

采取先确定敷设基准线，再按基准线沿指定的方向展开得到一组敷设参考线的生成原则，发现基准线的选取随着船体外表面部位的不同而不同，由此构建按参考线敷设法敷设矩形块的新流程：建立船体三维曲面模型→划分敷设区域→确定敷设基准线→产生敷设参考线→按参考线布置矩形块，见图1 所示。

对按参考线敷设法的关键——曲面敷设参考线的生成算法进行了研究，提出了曲面线偏移的概念和3 种实现算法，并通过分析比较详细讨论了3 种算法的优缺点。

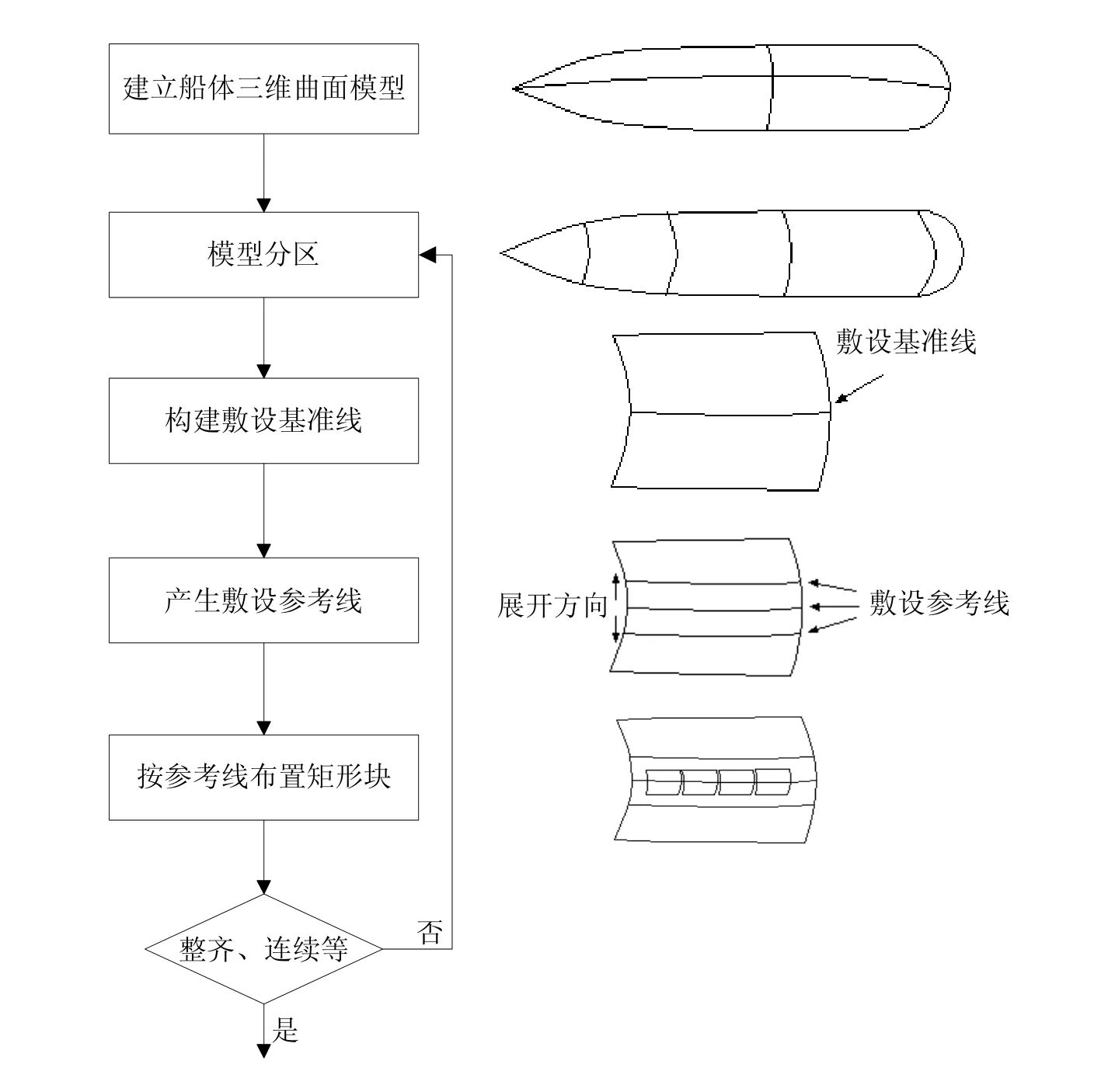
图1 按参考线敷设法流程图

1 算法描述

曲面线偏移，是依据平面线偏移的特性而定义的一个新概念，它同平面偏移线具有类似的特性，曲面偏移线上的每一个点到原曲面线的弧长距离都等于一个定值，同样也称为偏移距离，如图2 中d 所示。

要实现曲面线偏移算法，有两种思路：一种是将曲面展开成平面，如图3 所示，在展开面上先完成平面线偏移计算，然后再将平面偏移线映射回曲面，得到曲面偏移线，这种方法称为展开平面偏移算法；另一种思路则是先将曲面线依据计算精度离散为相互间存在拓扑关系的多个离 散点pi，再将每个离散点按偏移距离在曲面上计算得到对应的曲面偏移点Qi，如图4 所示，最后 将这些偏移点按其对应离散点的拓扑关系顺序连接，从而生成原曲面线对应的曲面偏移线，这种方法称为离散点偏移算法。

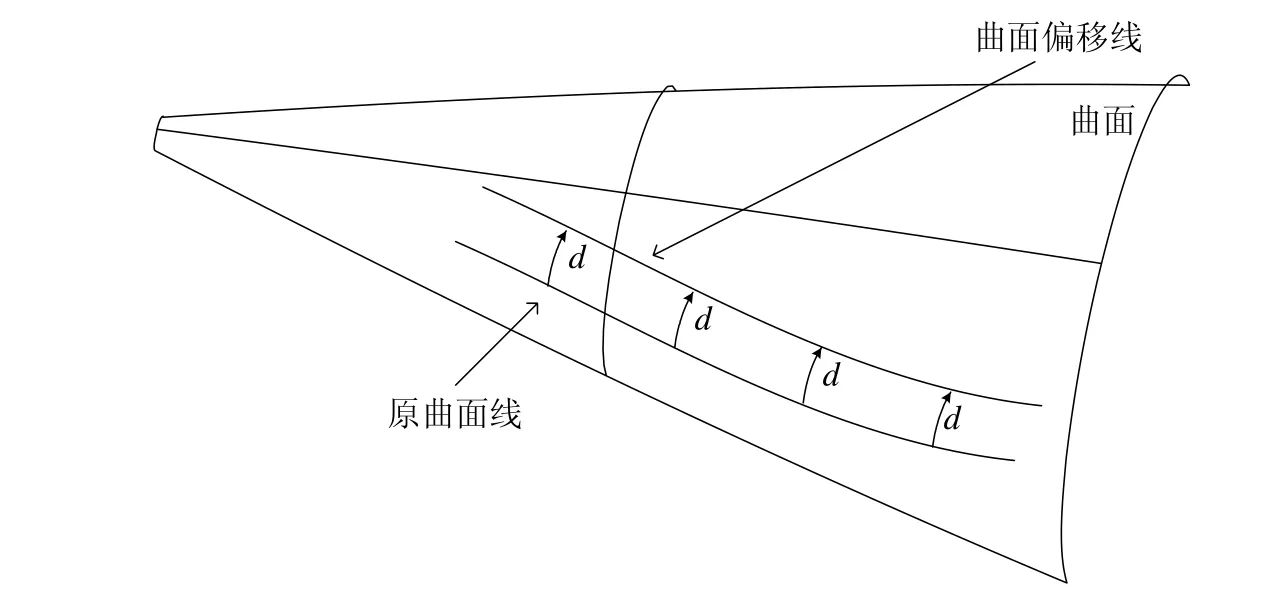
图2 曲面线偏移

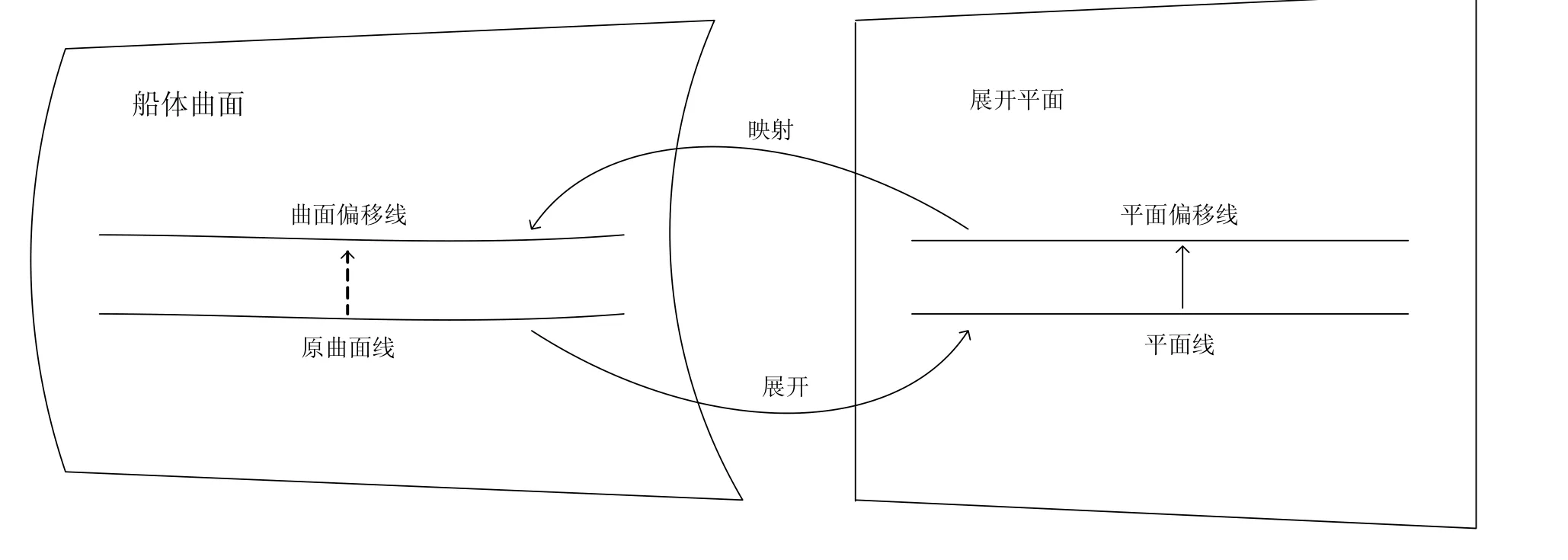
图3 展开平面偏移算法

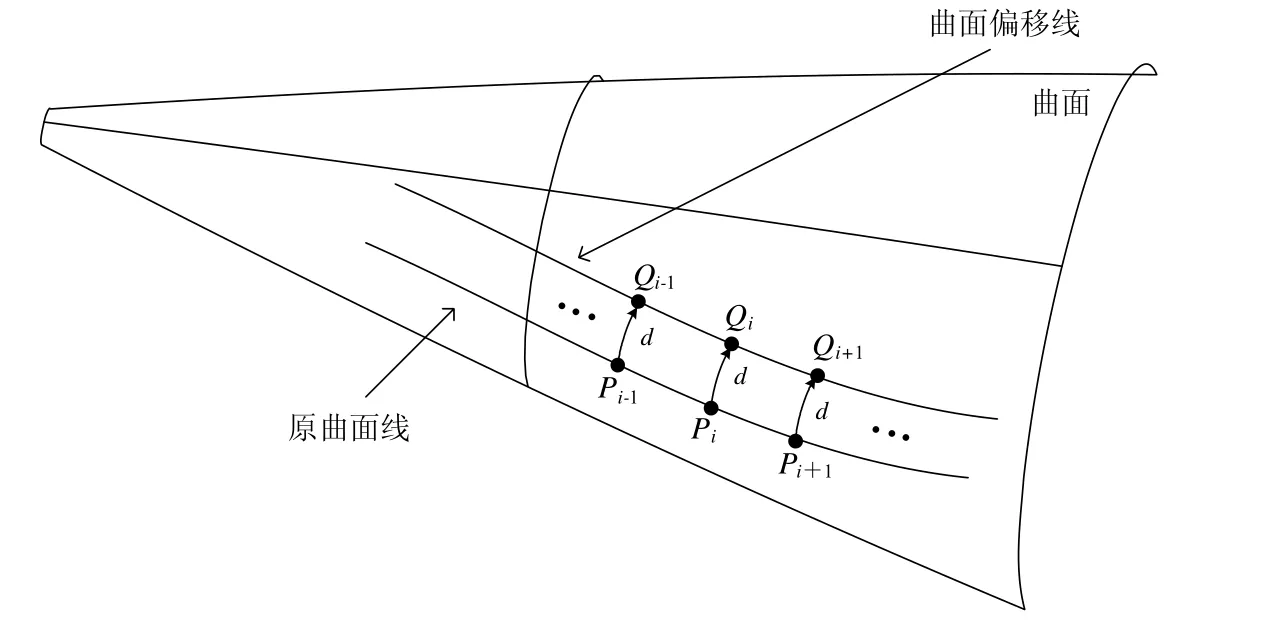
图4 曲面离散点偏移算法

展开平面偏移算法由于存在将曲面线映射到平面得到平面线和将平面偏移线映射回曲面得到曲面偏移线的运算，造成两次运算误差的积累，不能满足精度的要求。采用四边形网格等面积曲面展开改进算法[2]进行验证，所得到的曲面偏移线结果并不理想，特别是当曲面线很长时存在很大的问题，误差较大。鉴于以上原因，采用离散点偏移算法来实现曲面线偏移。

曲面离散点偏移算法的关键在于获取曲面线上存在拓扑关系的离散点和通过曲面偏移距离在曲面上计算得到曲面偏移点。

为了使离散点满足曲线的拓扑关系，由离散点顺次连接的线段应该能够很好地逼近曲线，目前常用的曲线离散化处理方法主要有等间隔法、等弦长法和等误差法[3]。如图5 所示，等间隔法是在允许偏差范围内，令各节点在x 轴上投影间距 xΔ 相等；等弦长法是在允许偏差范围内，令各节点间距离 LΔ 相等；等误差法是令各节点间曲线与逼近线段的误差δ相等。

图5 常用曲面离散化方法

由于所要偏移的矩形块敷设基准线一般为船体曲面轮廓线和水线， 近似 NURBS（Non-Uniform Rational B-Spline）曲线[4]，在船体分区范围内曲率变化不大，在进行离散处理时可以按等间隔法取点的方式得到离散点。

对于等间隔法中 xΔ 的选取，应能满足在曲线曲率大处（曲率半径小处）有足够多的离散点以减小逼近误差，而当离散点取得越多，则越能代表原曲线，精度越高。该方法思路简单，求取点的速度较快，易于实现。

在获得相互之间存在一定拓扑关系的离散点之后，求取每个离散点在给定曲面偏移距离所对应的曲面偏移点，经研究有两种较为可行的实现方法，分别为法平面交线算法和正交线离散点算法，下面逐一进行介绍。

1.1 法平面交线算法

将曲面线上离散点记为iP，该点的曲线切向为t ，曲面法向为n ，计算可得方向矢量tp= ( n × t )×n，一般情况下 tp与t 基本一致；以pt 为法向在点iP 生成平面，如图6 所示，该平面与曲面的交线记为il ；在il 上按偏移方向从iP点开始，取曲线距离等于偏移距离d 的点iQ ，它即为所求的曲面偏移点。

图6 法平面交线算法

1.2 正交线离散点算法

首先将离散点iP 作为求取正交线离散点的起点 R0，定义方向 d0= n0×ti，式中 n0表示 R0点的曲面法矢， ti表示点 Pi的曲线切矢，然后执行以下步骤，如图7 所示：

（1） 自0R 点沿着0d 方向取距离step，得到点0S ，step 表示计算步长，它决定了程序的计算精度，在计算时给定；

（2） 将0S 点垂直降落在曲面上，落点记为1R ，其与起点0R 之间的曲面距离取为 0D ；

（3） 将落点 R1置为起点，并计算方向 d1，其中 d1= (n1× d0)×n1，式中 n1表示 R1点的曲面法向矢量；

（5） 顺序连接离散点0R ，1R ，2R ，…生成曲线il ，并在该曲线上获取从首端点0R 开始弧长为偏移距离d 的点iQ ，该点即为所求的曲面 偏移点。

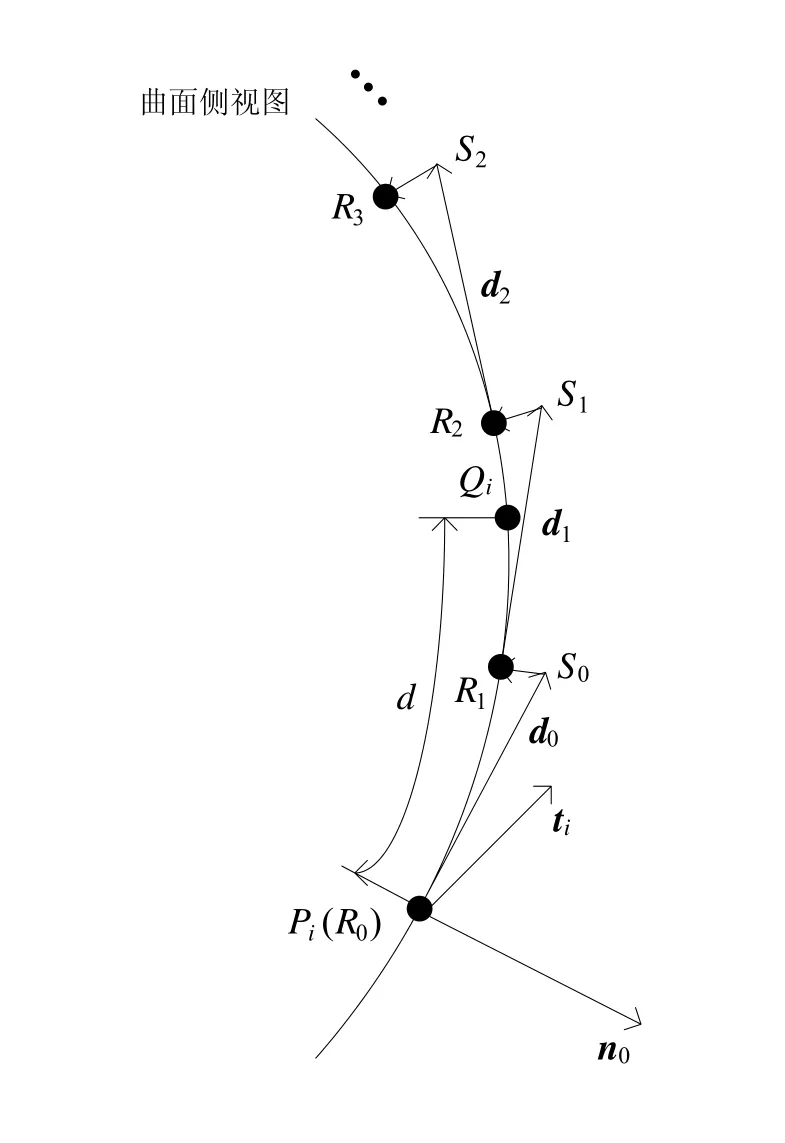
图7 正交线离散点算法

1.3 两种算法的分析比较

从算法的难易程度方面考虑：正交离散点算法较易实现，它只涉及到矢量运算和点到曲面的垂直落点问题；法平面交线算法则难于实现，虽然它的思路简单，但涉及到曲面与平面的求交问题，计算复杂度高。

从算法的精度和误差方面考虑：法平面交线算法只考虑了曲面在一点的拓扑关系，而正交点离散算法则使用多点逼近。因此，法平面交线算法没有正交离散点算法的精度高。

由上述可知，正交离散点算法计算精度较高，而且计算复杂度不高，很容易实现。因此，将采用正交离散点算法来实现曲面线偏移生成算法。

2 参考线生成实例与讨论

以正交离散点算法为基础，在MDT 系统中进行了二次开发，利用矩形块生成算法，选取部分船体后尾部曲面进行敷设设计，得到了一组曲面偏移线和矩形块，如图8 所示。

从图中可以看出，矩形块敷设参考线沿船长方向，在肋骨线方向近似等距，以此为基准敷设的矩形块能够满足整齐、美观、连续等要求，见图9 所示。

船体曲面矩形块按参考线敷设法改变了矩形块敷设体系，在生产设计环节，替换了原有在二维展开图上进行敷设设计的方法，形成了矩形块三维敷设设计的能力，实现了矩形块模拟敷设的快速化和自动化，将原有单一全船草方案工期从3 人3 月缩至1 人3 周。与二维敷设方法布置设计方案与实船敷设结果差异较大相比，按参考线敷设法能够将实船敷设结果可视化，实现了敷设效果的预先控制。

实际使用验证表明，由该方法得到的模拟敷设结果满足工程使用和精度的要求。

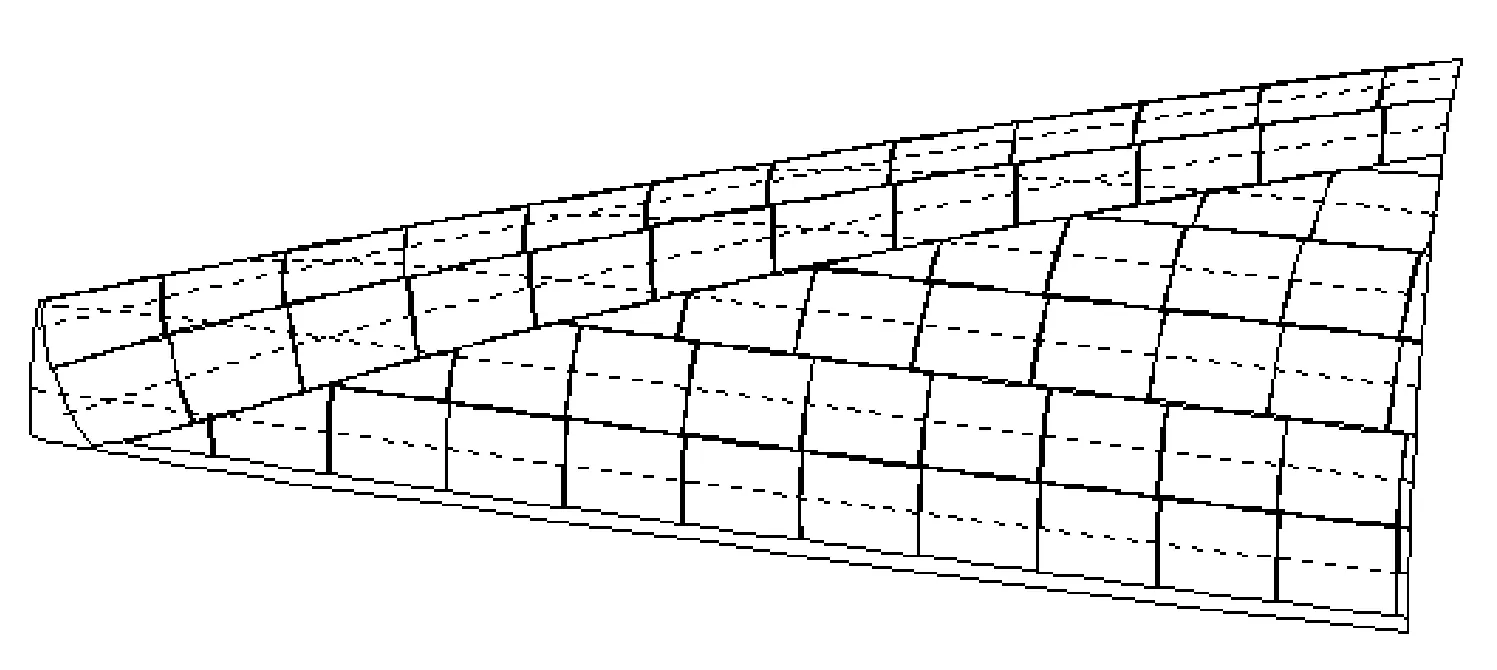
图8 船体后尾部曲面矩形块布置图

图9 船体后尾部曲面矩形块布置局部放大图

[1] 陈志飚, 赵 耀, 严 俊.船体曲表面敷设矩形块生成算法研究[J]. 工程图学学报, 2007, 28(1)： 83-88.

[2] 陈志飚, 赵 耀, 严 俊. 船体曲面柔性敷设块的展开[J]. 工程图学学报, 2006, 27(1)： 119-123.

[3] 刘丹丹, 张树有, 刘元开, 等. 一种基于特征点识别的曲线离散化方法[J]. 中国图象图形学报, 2004, 9(6)： 755-759.

[4] 施法中. 计算机辅助几何设计与非均匀有理B 样条(CAGD&NURBS)[M]. 北京： 北京航空航天大学出版社, 1994. 319-323.