一种新的Multiquadric 拟插值

陈荣华 ， 韩旭里， 吴宗敏

（1. 湖南科技大学数学与计算科学学院，湖南 湘潭 411201； 2. 中南大学数学科学与计算技术学院，湖南 长沙 410083；3. 复旦大学数学科学学院，上海 200433）

Multiquadric (MQ)是Hardy 于1968 年提出来的一种径向基函数(radial basis function)[1]。Hardy的一篇关于MQ 的论文[2]于1971 年发表后，MQ逐渐引起各国专家学者的研究兴趣，到1988 年，MQ 已经在大地测量学(geodesy)、地球物理学(geophysics)、测绘学(surveying and mapping)、摄影测量学(photogrammetry)、遥感与信号处理(remote sensing and signal processing)、地理学(geography)、地质与采矿(geology and mining)、数字地形模型(digital terrain models)以及水文学(hydrology)等诸方面都得到了应用[1]。自从Hardy[1]及Kansa[3-4]的综述性文章发表后，越来越多的专家学者对MQ 进行了深入细致的理论研究和范围广泛的实际应用，出现了许多关于MQ 的理论和应用的论文。

Franke 在其评论文章[5]中指出：就精度 (accuracy)、稳定性(stability)、有效性 (efficiency)、内存需要(memory requirement) 和易于实现(ease to implementation) 而言，MQ 在所有29 种散乱数据插值格式中首屈一指。

应用MQ 求解微分方程的文章也很多，如Wu 用MQ 拟插值求解双曲型(hyperbolic)方程[6]，Hon和Mao用MQ 求解抛物型(parabolic)方程[7]，Fedoseyev、Friedman 和Kansa 用MQ 求解椭圆型(elliptic)方程[8]都取得了很好的结果。

MQ 拟插值目前已知的有4 种，即，Beatson 和Powell 的LA、LB和 LC[9]以及Wu 和Schaback的 LD[10]。

本文给出了一种新的MQ 拟插值，分析了其具有的性质以及其逼近度。根据本文给出的数值实验可知，该拟插值确实具有良好的逼近精度和保形性。此外，它还至少可用于求解双曲型和抛物型方程，关于这一部分内容将在以后的论文中介绍。

1 Multiquadric 拟插值的构造及其性质

Beatson 和Powell 于1992 年提出了3 种Multiquadric (MQ)拟插值，即 LA、 LB和 LC，并给出了它们的逼近阶[9]。其中，LB是常数再生的，LC是线性再生的；而 LA不是常数再生的，LB不是线性再生的。

Wu 和Schaback 指出AL 和BL 不具备保线性性和保凸性，证明了CL 具备保线性性和保凸性， 构造了另一类具备保线性性和保凸性的MQ 拟 插值DL ，并给出了其逼近阶[10]。

由于DL 的逼近精度不比CL 的逼近精度低，而且，在构造DL 时不需要给定端点处的一阶导数而在构造CL 时却要给定端点处的一阶导数，所以，从构造拟插值需要条件的多少来衡量，DL明显优于CL 。

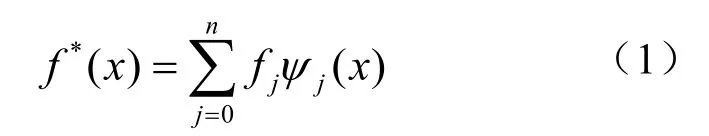
这里 ψj(x), j = 0, 1,…,n是某些选定的函数。

在构造拟插值之前，先给出几个定义：定义1 若拟插值 )(* xf 具有性质

其中 C 是任意给定的常数，则称该拟插值在[ x0,xn]上是常数再生的(constant reproducing)。

定义2 对任何 ,p q R∈ ，当 qpxxf +=)( 时，拟插值 )(* xf 满足 qpxxf +=)(*，则称该拟插值在[ x0,xn]上具有线性再生性(linear reproducing)。

由以上定义可知，具有线性再生性的拟插值必定是常数再生的。

定义3 对于单调增加（减少）的数据jf , j = 0, 1,…,n ，如果拟插值 f*(x)是单调增加（减少）函数，则称该拟插值在 ],[0nxx 上具有保 单调性(preserving monotonicity)。

取如下形式的ψj(x)

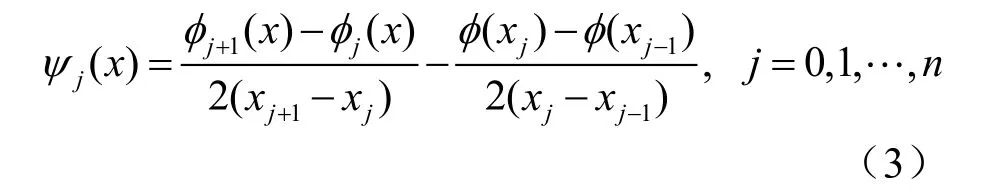
得到拟插值 f*(x)具有以下性质。

定理1若取 则由式(1)、式(3)定义的拟插值 )(* xf 在 ],[0nxx 上具有线性再生性，而且， )(* xf 在 ],[0nxx 上可改写为如下3 种等价的形式

此外，在 ],[0nxx 上，有

及

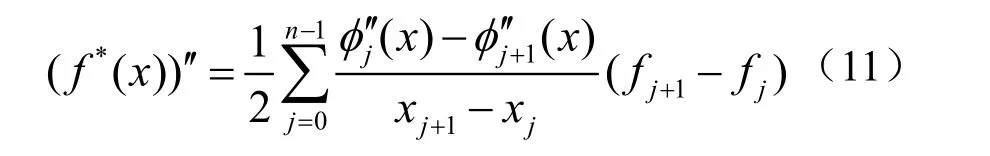
而且，更一般地，有

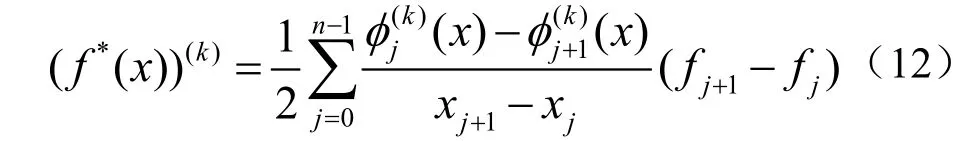
证 明首先，由式(1)及式(3)可得

再由式(4)及式(6)可知式(8)成立。通过计算不难发现式(7)、式(8)与式(9)三者等价。对式(8)两边关于x 求一阶、二阶和k 阶导数，就分别得到式(10)、式(11)及式(12)。要证明线性再生性，只要证明

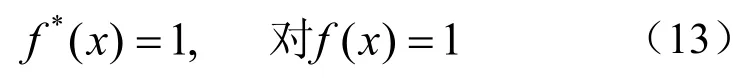
及

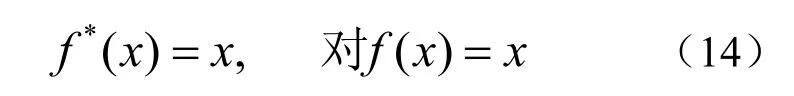
由式(9)易知式(13)成立，由式(9)及式(5)可知式(14)成立。定理证毕。

注1由上述定理的证明过程可以看出，式(7)～式(12)及常数再生性成立，不需要式(5)成立这一条件。

定义4由式(1)、式(3)、式(4)、式(5)、式(6)及下式

定义的拟插值就是在本文中定义的新的MQ 拟插值。

由上述定义得到的MQ 拟插值具有如下性质：

定理 2由定义4 得到的MQ 拟插值 f*(x)在 [ x0,xn]上具有线性再生性、保单调性，并且，在 [ x0,xn]上有式(7)～式(12)成立。

证 明由定理1，只要证明由式(1)、式(3)、式(4)、式(5)、式(6)及式(15)定义的MQ 拟插值 f*(x)在 [ x0,xn]上具有保单调性就可以了。Wu 和Schaback[10]已经证明了。

对j =1,…, n −1, 有 −1 ≤ φ ′j( x) ≤φ ′j−1( x) ≤1而由式(5)，有

因而

对j = 0, 1,…, n −1, 都有φ ′j( x) −φ ′j+1( x) ≥ 0

最后，由式(10)就完成了定理的证明。

则 对 任 何 实 数 c ＞ 0, x∈[x0,xn]及 函 数f ( x)∈ C2(x0,xn)，由定义4 得到的MQ 拟插值f*(x)满足

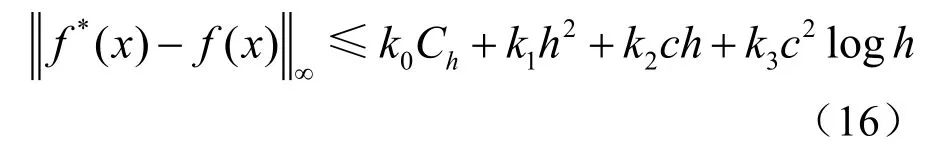
其中

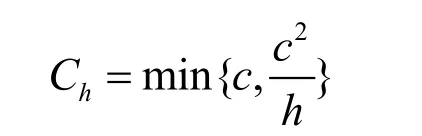
k0, k1,k2,k3是不依赖于h 和c 的常数。

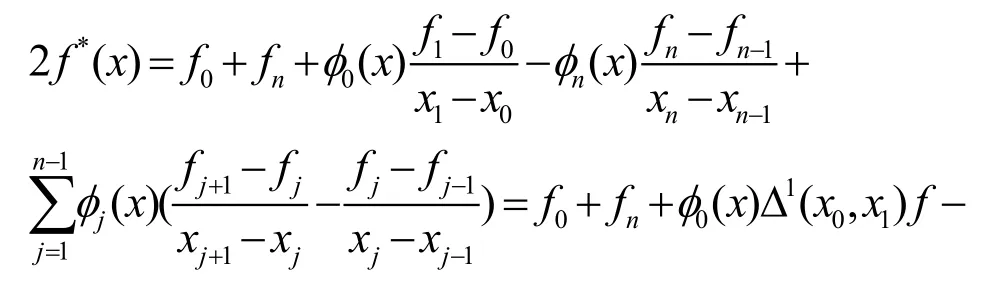
证 明由式(9)，有 其中1Δ 及2Δ 分别为一阶和二阶差商算子，由f ( x)∈ C2(x0,xn)可知，上述一阶和二阶差商都是有界的。若用 )(xL 表示关于 )(xf 的与 )(* xf 具有 相同已知数据的分段线性插值，则

其中

于是

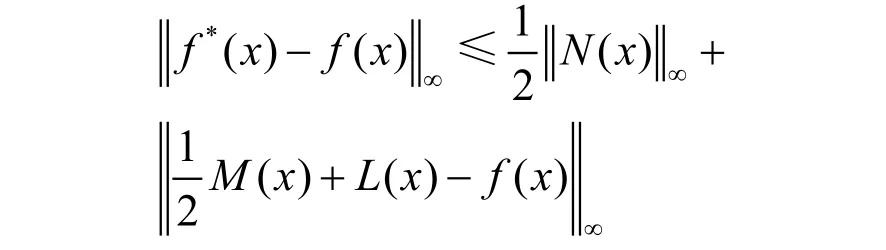
Wu 和Schaback 在文献[10]中给出了

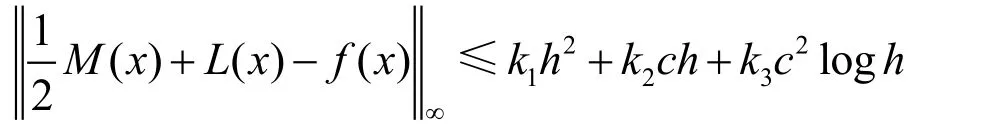
及

因此，又有

于是，式(16)成立。

注2定理3 的证明中利用了如下结论：当 x∈ [ x0,xn]时，有

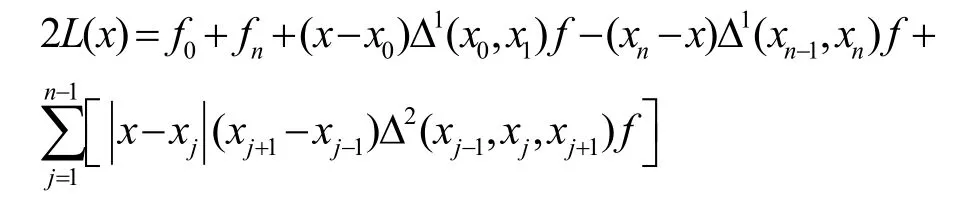
2 算 例

考虑对函数f(x)=sin(x)在区间 [0, 2π]上的MQ 拟插值。

图1 h = 时MQ 拟插值的计算结果

图2 h =时MQ 拟插值的计算结果

此外，就函数f(x)= cos(x)在区间 [0,2π]上的MQ 拟插值进行了类似的数值实验，得到的结论与上述结论类似，相应的误差向量的无穷范数分别 为 0.021854, 0.0054496, 5. 3476× 10−5和2. 7685× 10−5。

3 结 论

通过分析发现：由式(1)、式(3)、式(4)、式(5)及式(6)定义的拟插值在所讨论的区间上具有线性再生性，且式(7)～式(12)成立。由上述定义的拟插值若还满足式(15)，那么它就是本文所介绍的一种新的MQ 拟插值，它除了具有上述拟插值所具有的性质外，还具有保单调性，而且其逼近误差可用式(16)来估计。

数值实验的结果证实了该拟插值确实具有良好的逼近精度和保形性。

[1] Hardy R L. Theory and applications of the multiquadric-biharmonic method, 20 years of discovery 1968-1988 [J]. Computers Math. Appl., 1990, 19(8/9)： 163-208.

[2] Hardy R L. Multiquadric equations of topography and otherirregular surfaces [J]. Geophysical Res., 1971, 76： 1905-1915.

[3] Kansa E J. Multiquadric-a scattered data approximation schemewith applications to computational fluid dynamics, Ⅰ, Surface approximations and partial derivative estimates [J]. Computers Math. Appl., 1990, 19(8/9)： 127-145.

[4] Kansa E J. Multiquadric-a scattered data approximation scheme with applications to computational fluid dynamics, Ⅱ, solution to parabolic, hyperbolic and elliptic partial differential equations [J]. Computers Math. Appl., 1990, 19(8/9)： 147-161.

[5] Franke R. Scattered data interpolation： test of some methods [J]. Math. Comput., 1982, 38： 181-200.

[6] Wu Z M. Dynamically knots setting in meshless method for solving time dependent propagations equation [J]. Comput. Methods Appl. Mech. Engrg., 2004, 193： 1221-1229.

[7] Hon Y C, Mao X Z. An efficient numerical scheme for Burgers' equation [J]. Appl. Math. Comput., 1998, 95： 37-50.

[8] Fedoseyev A I, Friedman M J, Kansa E J. Improved multiquadric method for elliptic partial differential equations via PDE collocation on the boundary [J]. Computers Math. Appl., 2002, 43： 439-455.

[9] Beatson R K, Powell M J D. Univariate multiquadric approximation： quasi-interpolation to scattered data [J]. Constructive Approximation, 1992, 8： 275-288.

[10] Wu Z M, Schaback R. Shape preserving properties and convergence of univariate multiquadric quasi-interpolation [J]. ACTA Math. Appl. Sinica, 1994, 10(4)： 441-446.