消除零级衍射和循环移位改善计算机合成 全息图的再现质量
刘 敏, 杨光临, 谢海燕
(1. 北京大学区域光纤通信网与新型光通信系统国家重点实验室,北京 100871; 2. 中科专利商标代理有限责任公司,北京 100083)
本文针对计算机合成全息图再现象质量问题[1],分析了影响再现象质量的主要因素,并提出了一种能有效改善合成全息图再现象质量的方法。
采用数字图像去计算合成全息图,在信息安全方面有着广泛应用,如,数字全息水印技术[2-7]。但是,其再现理论,基本上都是从光学理论直接借鉴过来的,是基于模拟域。而采用数字图像去合成全息图的制作和再现都是用计算机处理的,完全建立在数字域。数字域和模拟域的理论虽然相似,但是,不能完全等同。例如,光信息处理中连续两个透镜的作用等同于成倒立虚像,但计算机处理中数字图像经过连续两次离散傅里叶变换得到的是原图像的上下左右颠倒的虚像,并且有一行和一列的循环移位(图1(b))。可见,在数字域从理论上分析合成全息图的再现情况是必要的,而且很有用处。
本文在得到Burch 型合成全息图再现的数学表达式后,利用计算机处理的灵活性,调整虚像的像素位置消除循环移位,同时,消除再现的零级衍射,从而不需要通过取对数来显示再现象,使得Burch 型合成全息图能够精确恢复原图像。
1 Burch 型合成全息图原理
根据Burch 型合成全息图的原理[6],其合成全息图的透过率函数为

这里 ( , )B x y 是物函数振幅函数的归一化结果,α表示参考光的载频。
根据空间带宽积的要求,Burch 型合成全息 图的傅里叶抽样数 M=β1m, N = β2n必须满足

m、n 是原数字图像的像素大小。
2 Burch 型合成全息的再现原理
为了模拟光学全息中毛玻璃的漫散射特性,数字图像 ( , )I p q 在傅里叶变换前乘以随机位相rand ( p, q) ∈ (0,1),得到 I ′( p, q) = I ( p, q) ej⋅2π⋅rand(p,q), I ( p , q )的傅里叶合成全息图记录的是 I ′( p, q)的傅里叶变换谱,即


由式(1)可以得到

考虑到傅里叶变换与其反变换的关系,有

那么

那么

MN ⋅δ (1,1)不是严格意义上的冲击函数,这里表示只在点(1,1)有值。
虽然上式中后两项都是复数,但只要保证它们在再现平面上不会交叠,就可以分别对三项取模,

图 1 连续两次DFT的循环移位作用
于是上式可以化简得
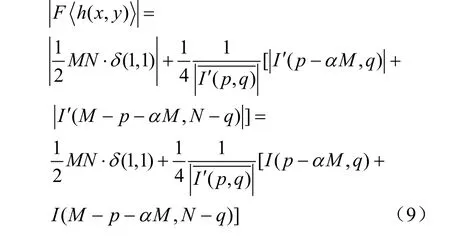
3 实验分析
3.1 离散傅里叶变换产生循环移位
根据二维离散傅里叶变换的性质,若对数字图像 ( , )I p q 的傅里叶变换的抽样单元数为M N× ,则

在光学全息中,透镜的作用相当于傅里叶变换,连续两次DFT 的作用相当于经过两次光学透镜作用后成倒立虚像。但是,需要指出的是,由于DFT 的循环移位作用,使得虚像的最后一行和最后一列被分别循环移位到第一行和第一列。从图1(b)的被圈出来的区域:最左边的黑线以及最上边的黑色区域可以看到循环移位的存在,这正是图1(a)虚像的最后一行和最后一列分别循环移位到第一行和第一列的结果。
3.2 消除零级衍射和循环移位再现象
MN ⋅δ (1,1)是冗余信息,对再 现象没有贡献,且严重降低了再现图像的对比度,因此将它去掉得到下式
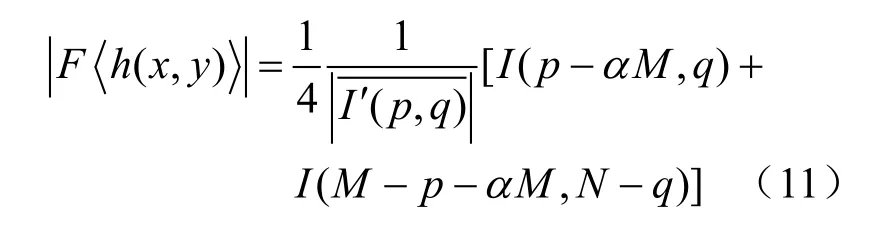

消除零级衍射后,再通过调整再现虚像的像素位置消除循环移位,使得Burch 型合成全息能精确恢复原图像。
图2 是抽样倍数 β1= 2, β2=2的全息图2(a) 及常规再现图2(b)的情况,图2 (b)的顶端就是很明显的循环移位;通过去掉零级衍射后得到图3 (a),其中间有很明显的循环移位,于是通过调整像素位置消除循环移位后得到图3(b),Burch 型合成全息图再现得到精确的实像和虚像。


图 2 合成全息图和传统再现图像

图 3 消除零级衍射和循环移位改善再现质量图像

表1 对应像素位置像素值的比值
4 结 论
本文在数字域推导了采用数字图像去合成Burch 型全息图的再现表达式,指出了影响再现质量的两个因素,一是零级衍射作为冗余量严重降低了再现象的对比度,另一个原因是连续两次DFT 变换使得再现的虚像产生一行和一列的循环移位。于是,通过调整虚像像素的位置消除循环移位和消除零级衍射,有效地提高了再现象的对比度,理论和实验都证明了,这种方法能够使得Burch 算法精确地恢复原图像。本文提出的再现方法也同样能够有效地提高黄氏和李威汉型合成全息图再现象的质量。
[1] Yang Guanglin, Xie Haiyan. An approach compress information of computer-synthesis hologram with shape adaptive binary tree predictive coding and fast Fourier transform technique [J]. IEEJ Trans. EIS. , 2005, 125(1): 99-105.
[2] Nobukatsu Takai, Yuto Mifune. Digital watermarking by a holographic technique [J]. Appl. Opt., 2002, 41(5): 865-873.
[3] Yoshinao Aoki. Watermarking technique using computer-generated holograms [J]. Electron. Commun. Japan 3, 2001, 84(1): 21-31.
[4] Hsuan T Chang, Chung L Tsan. Image watermarking by use of digital holography embedded in the discrete-cosine-transform domain [J]. Appl. Opt., 2005, 44(29): 6211-6219.
[5] Smirnov M V. Holographic approach to embedding hidden watermarks in a photographic image [J]. J. Opt. Technol., 2005, 72(6): 464-468.
[6] Burch J J. A computer algorithm for synthesis of spatial frequency filters [C]//Proc. IEEE, 1967, 55: 599-601.
[7] Liu Min, Yang Guanglin, Xie Haiyan, et al. Computer-generated hologram watermarking resilient to rotation and scaling [J]. Opt. Eng., 2007, 46(6): 060501-060503.

