卫星转动条件下APS星敏感器星像目标中心提取精度分析
李 晓,赵 宏
(1.北京控制工程研究所,北京 100190;2.中国空间技术研究院,北京100094)
卫星转动条件下APS星敏感器星像目标中心提取精度分析
李 晓1,赵 宏2
(1.北京控制工程研究所,北京 100190;2.中国空间技术研究院,北京100094)
目前对星敏感器星像定位的研究多限于静态情况,而卫星转动过程中,在曝光期间星像在像平面不断移动,从而影响星像定位的精度,重点分析动态情况下APS星敏感器星像目标中心的提取精度.首先分析采用质心法计算星像目标中心的误差源,提出动态精度的估计方法,并推导相应的计算公式;进而以给定的APS星敏感器参数为基础,研究了计算窗口、曝光时间等精度影响因素的选择方法;最后通过仿真进行了验证.
动态精度;星像目标中心;APS星敏感器;质心法
星敏感器是当今航天器广泛采用的一种高精度高可靠性的姿态测量器件,它通过探测天球上不同方位的恒星来确定航天器相对于惯性坐标系的三轴姿态.
星敏感器星像位置的定位精度不仅关系到姿态计算的精度,还影响到星图匹配的准确率.为提高星像定位精度,星敏感器采用离焦的光学系统将星像覆盖几个像元,然后通过质心法、曲面拟和法等内插细分算法确定星像中心位置,使星像定位精度达到亚像元或更高的精度.文献[1-3]研究了静态情况星像中心的提取算法和相应的精度.
在动态情况下,由于角速度的影响,曝光期间星像在像平面不断移动,从而影响星像定位的精度,但目前关于这方面的研究较少.本文根据APS像元输出模型,研究了角速度小于2(°)/s时采用质心法提取星像目标中心的精度,并在此基础上分析了计算窗口和曝光时间对星像目标中心提取精度的影响.
1 APS像元输出模型
APS星敏感器像元噪声有多种,为简化分析过程,只考虑暗电流噪声、光子散粒噪声、读出噪声、背景噪声和量化噪声,而将其他噪声一并归入读出噪声进行分析.
像元产生的电荷数可用如下的随机变量来表示[4]:

式中,Ns表示有效信号产生的电荷数,近似看作高斯分布的随机变量,其均值为 μs,标准差为代表光子散粒噪声对信号的影响;Ndark表示暗电流产生的电荷数,近似看作高斯分布,均值为 μdark,标准差,是暗电流噪声在输出中的体现;B为背景产生的电荷数,相当于10等星产生的电荷数[5],分析方法同 Ns;Nron为读出噪声,同样采用高斯分布近似,其均值为零,标准差σron由星敏感器厂家提供.因此像元产生的电荷数可以看作均值为μ,标准差为σ的正态分布

设像元输出灰度I与像元产生的电荷数N满足如下正比关系:
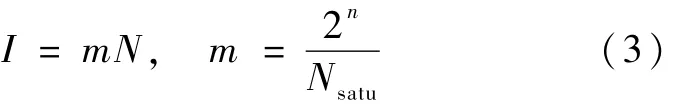
式中,m为比例系数,n为量化位数,Nsatu为饱和光电子数.量化过程中会产生服从0~1均匀分布的量化误差,其方差为1/12.因此像元输出灰度 I的均值E(I)和标准差为

设σquan为量化误差的等效电荷数
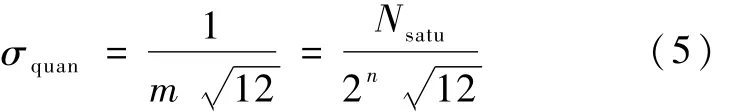
则像元输出灰度I的均值和标准差为
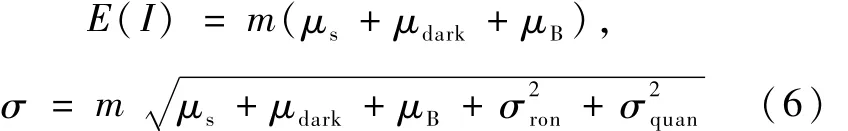
2 星像目标中心提取误差分析
在静态情况下,星像能量满足正态分布,点扩散函数可以用二维高斯函数来表示
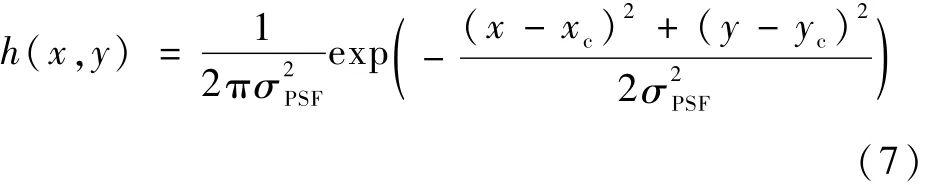
式中,(xc,yc)表示星像中心的实际位置,σPSF为高斯半径,表示点扩散函数的能量集中度.
角速度不为零时,由于在曝光时间段内星像中心一直在移动,星像能量分布可以用如下函数表示:

式中,Te为曝光时间,(xc(t),yc(t))为时刻 t(0≤t≤Te)的星像中心位置坐标.对其采用质心法得
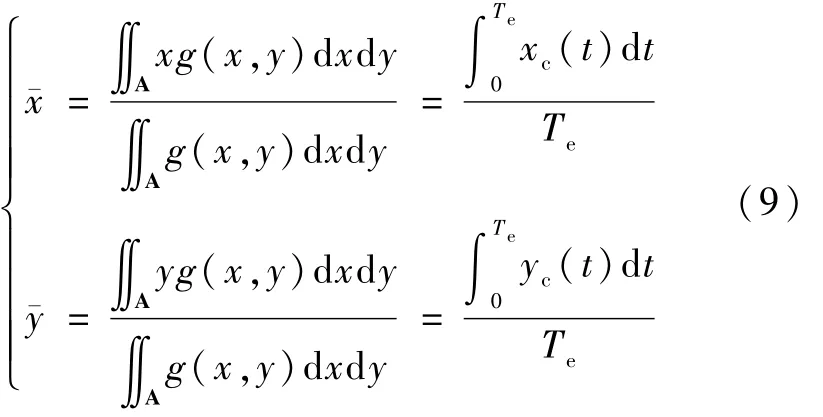
其中A为积分区域,理论上其范围应该是像平面所处的整个平面.
定义星像中心在 Te/2时刻所处的位置为星像目标中心.考虑到角速度一般在2(°)/s以内,曝光时间小于0.5 s,星像中心轨迹很短且近似为直线,xc(t),yc(t)可以认为是线性函数,因此·(Te/2)yc(Te/2).所以采用质心法提取星像目标中心是可行的.
采用质心算法提取星像目标中心的误差可分为两类:一类是质心算法自身的误差,称其为系统误差;另一类是由APS像元噪声引起的误差,称其为随机误差.
2.1 星像目标中心提取系统误差分析
采用质心算法计算星像目标中心位置坐标的系统误差有以下3个方面:
1)由于 xc(t)、yc(t)的非线性而带来的误差.
2)由于图像是离散的,用求和替代积分,会引入离散误差.式(9)近似为

式中,xk,yk为第 k像元的几何中心坐标;Ik为第 k像元的灰度值,与能量分布函数在相应区域的积分成正比.产生离散误差的原因是采用像元的几何中心代替能量分布函数的平衡点[2].
实际计算中不可能采用无限大像平面,而是采用一定的窗口区域As进行计算.即
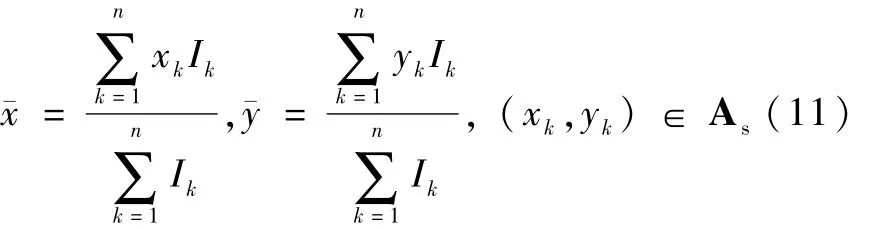
其中n为窗口区域内像元总数,用有限区域代替无限区域,会引入误差.在静态情况下,计算窗口一般采用5×5或3×3像元;因此在动态情况下,计算窗口As选择为5×5或3×3像元随星像中心移动而形成的区域,分别记为 As5和As3.
第二项系统误差可以认为是采用式(11)代替式(9)产生的误差,式(11)为采用质心法提取星像目标中心的最终表达式.
3)由于APS像元暗电流以及天空背景的影响,Ik自身测量带有系统误差,从而给计算结果带来系统误差.
由式(6)可知,未含有有效信号的 APS像元服从均值 In=m(μdark+μB)的正态分布,In近似等于图像的灰度均值E.采用式(11)计算星像目标中心时,为抑制第三项系统误差,计算窗口内的像元灰度应减去E.因此忽略第三项系统误差,并认为用于计算星像目标中心的像元灰度I的均值和标准差为

2.2 星像目标中心提取随机误差分析
采用式(11)计算星像目标中心的随机误差由APS像元噪声引起.由于分析¯x与¯y是等效的,下面仅以¯x为例分析该随机误差.设μ0为曝光期间产生的总信号电荷数,μsk为第 k像元的信号电荷数,Ik为第k像元的灰度期望值,Ik=mμsk,σk为第k像元的灰度值标准差,设

则根据式(8)能量分布函数积分可得

其中 Ask、As为积分区域,Ask为像元 k所处区域,As为计算窗口所处区域.
假定各像元的随机误差是不相关的,根据随机误差的传递公式可得¯x的方差

令

则

由式(14)可得
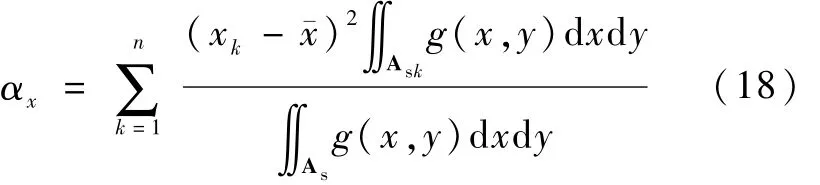
可以看出,αx、βx反映了 As区域的形状、大小、信号电荷分布对随机误差的影响,而与 μ0、μdark、μB、σron、σquan无关.
恒星在曝光期间产生的总信号电荷数μ0为

式中,E0=2.96×10-14W/mm2为零等星辐照度,Mv为星等,D为镜头口径,Eph为单个光子能量,Te为曝光时间,τ0为光学系统透过率,QE为量子效率,Kfill为填充系数.当计算窗口为As5时,窗口区域集中了99%以上的有效信号电荷,因此认为μs=μ0;当计算窗口为 As3时,窗口区域集中了约94%的有效信号电荷,因此认为 μs=0.94μ0.
暗电流μdark可以按如下公式计算:

式中,Jdark为暗电流密度,S为像元面积,q为一个电荷所带电量;背景噪声μB相当于10等星产生的电荷数;读数噪声 σron和量化噪声σquan为常数,可根据APS星敏感器的参数获得.
3 星像目标中心提取精度估计
考虑到星体角速度和曝光时间的范围,星像中心轨迹很短且近似为直线,因此忽略第一项系统误差,认为 xc(t),yc(t)是线性函数.设星像中心轨迹为线段L,其参数方程为

式中,u为星像中心移动速率,θ为轨迹与x轴夹角.
设 l为轨迹 L的长度,l=uTe.将式(21)带入式(8),并令积分变量t=τ/u得出信号电荷的分布函数

由式(22)可以看出,信号电荷的分布函数只与初始位置(x0,y0)、轨迹L的长度 l和轨迹与 x轴的夹角θ有关.
若轨迹 L的初始位置(x0,y0)、长度 l和与 x轴的夹角θ已知,可以确定计算窗口As;由式(22)进行数值计算可以得到信号电荷在As区域各像元的分布;根据式(11)可以计算¯x、¯y,与xc(Te/2)、yc(Te/2)比较可获得第二项系统误差;同时可以由式(16)和(18)计算 αx、βx,确定随机误差.
但实际情况中轨迹的参数是随机的,因此星像目标中心的系统误差和随机误差也是不确定的.对于系统误差,其在某一极限范围内具有随机性,性质上属于未定系统误差,因此采用标准差ex、ey来表征系统误差取值的分散程度;对于随机误差σ¯x、σ¯y,应计算其可能出现的最大值σ¯xm、σ¯ym.最终得到反映星像目标中心提取精度的量

由于 x方向与 y方向等效,则 σy=σx.
表1给定了APS星敏感器参数[1],下面以此为基础计算星像目标中心x方向的提取精度.
当计算窗口为A s5时,随机给定 L的参数并计算系统误差230次,图1为x方向的系统误差.根据这230个误差数据,计算出标准差ex=0.001像元.
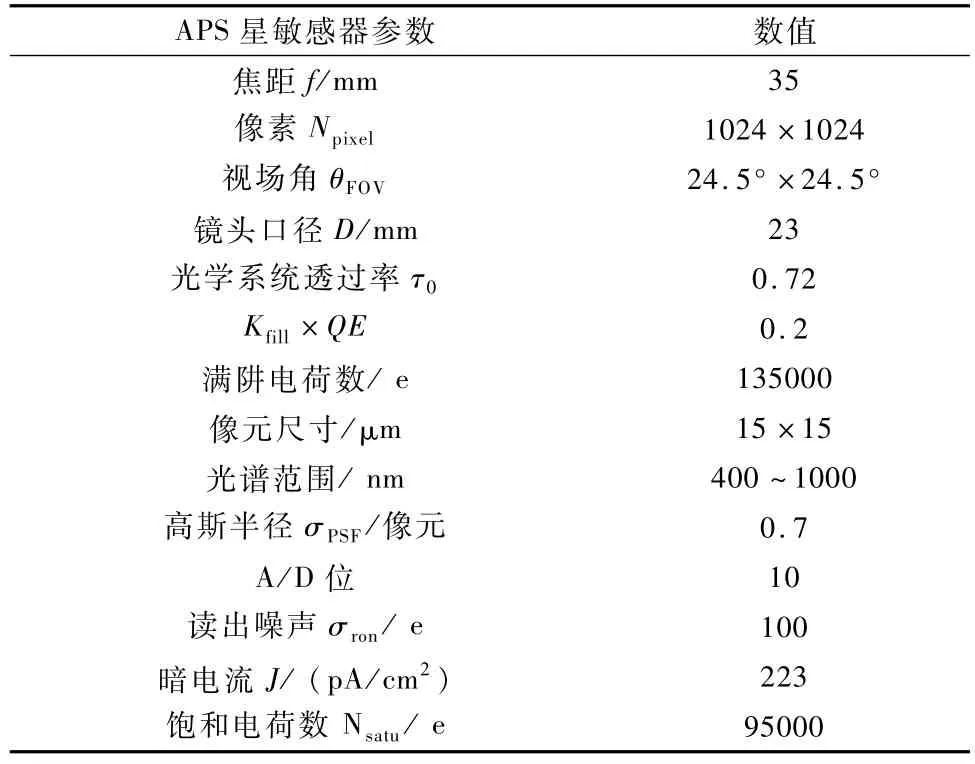
表1 给定APS星敏感器的参数
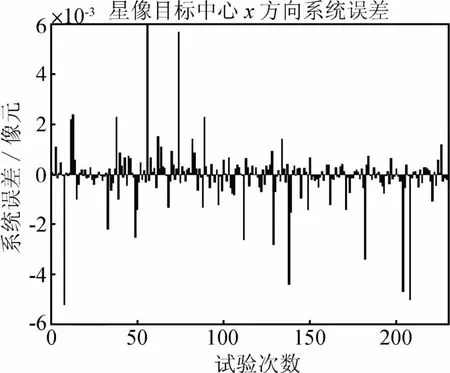
图1 计算窗口为A s5时星像目标中心x方向的系统误差
同理,当计算窗口为 As3时,随机给定L的参数并计算系统误差230次,结果见图2,计算出标准差ex=0.025像元.

图2 计算窗口为A s3时星像目标中心x方向的系统误差
在角速度的模ω和曝光时间Te一定的情况下,当角速度方向与测量坐标系的y轴平行时,星像轨迹平行于x轴,αx、βx取得最大值αxm、βxm,从而σ¯x取得最大值σ¯xm.因此计算σ¯xm时,应假定角速度方向平行于y轴.此时θ=0,轨迹长度l可根据角速度的模和曝光时间估计

式中,l的单位是像元,θFOV表示视场角,Npixel为像平面每行或每列的像元数.由于初始位置(x0,y0)对αx,βx影响不大,因此 αxm,βxm与轨迹长度 l的函数关系可通过多项式拟和获得.对于给定的APS星敏感器,计算窗口为A s5时,αxm,βxm值与轨迹长度 l的函数关系为

计算窗口为As3时,αxm,βxm值与轨迹长度l的函数关系为

因此,给定曝光时间 Te,星等 Mv,角速度ω,由式(17)、(24)、(25)可以计算A s5窗口下 x方向的随机误差上限σ¯xm,由式(17)、(24)和(26)可以计算A s3窗口下x方向的随机误差上限σ¯xm.最终由式(23)得到星像目标中心 x方向提取精度 σx.图3和图4分别给出了3等星和5等星在两种计算窗口情况下σx的计算结果.通过比较可以看出:选用 As3窗口效果较好.
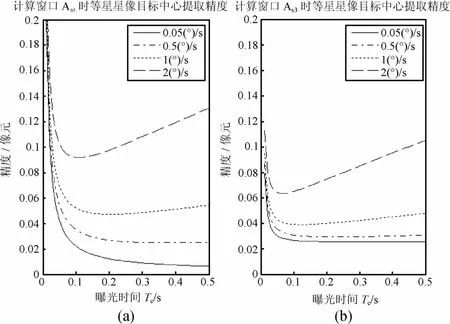
图3 3等星的星像目标中心提取精度
4 最优曝光时间
在静态情况下,曝光时间越长,信噪比越高,质心提取精度越高.在动态情况下,随着曝光时间的增加,信号电荷μs增加,但信噪比却没有增加,星像目标中心提取精度不一定提高.从图3和图4也可以看出,σx随曝光时间的增加是先减后增的变化趋势,因此存在最优的曝光时间使得星像目标中心提取精度最高.

图4 5等星的星像目标中心提取精度
给定星等Mv,角速度ω,由第四节的分析可知σx是Te的函数,可以通过求导的方式得到最优的曝光时间,也可通过数值计算求出最优曝光时间.图5给出了给定的星敏感器采用A s3窗口时,2~6等星的最优曝光时间随角速度ω的变化而变化.
可以看出,星等对最优曝光时间的影响不明显.经过计算比较,从2等星到6等星,最优曝光时间的变化范围不超过20%.而对于一定的星等,曝光时间在最优曝光时间附近20%范围的变化对星像目标中心提取误差的影响不超过1%.因此选择2~6等星最优曝光时间的平均值作为星敏感器的最优曝光时间.考虑到曝光时间不宜超过0.5 s,因此最优曝光时间的上限为0.5 s.

图5 2~6等星的最优曝光时间
图6 给出了不同的星等在最优曝光时间下的星像目标中心提取精度.可以看出,角速度小于2(°)/s,星等小于5时,通过调整曝光时间可以使星像目标中心提取精度保持在0.4个像元以内.

图6 最优曝光时间下的星像目标提取精度
5 数学仿真
仿真以表1的 APS星敏感器参数为基础,给定测量坐标系y轴方向的角速度,在星等、曝光时间确定的情况下,随机产生星矢量1000次,计算星像目标中心x方向的提取误差的均方根.图7和图8分别显示了3等星和5等星在不同的计算窗口和不同曝光时间下星像目标中心x方向误差的均方根.

图7 3等星的星像目标中心x方向误差的均方根
从仿真结果可以看出采用A s3窗口星像目标中心提取误差较小;与图3和图4相比较,可以看出误差大小及其随曝光时间的变化趋势与理论计算值基本相符.

图8 5等星的星像目标中心x方向误差的均方根
6 结 论
本文分析了采用质心法计算星像目标中心的系统误差和随机误差,提出了动态情况下星像目标中心提取精度的估计方法,并推导出相应的计算公式.进而采用此精度估计方法对给定的APS星敏感器进行分析,并经过仿真验证得出如下结论:
(1)采用A s3计算窗口精度较高;
(2)不同角速度存在不同的最优曝光时间,使得星像目标中心提取精度最高,可由精度计算公式对曝光时间求导得出;
(3)当角速度小于 2(°)/s,星等小于 5时,通过调整曝光时间可以使星像目标中心提取精度保持在0.4个像元以内.
[1]董瑛,邢飞,尤政.基于CMOSAPS的星敏感器光学参数确定[J].宇航学报,2004,25(6):663-668
[2]李玉峰,郝志航.星点图像超精度亚像元细分定位算法的研究[J].光学技术,2004,31(5):666-671
[3]李春艳,谢华,李怀锋,孙才红.高精度星敏感器星点光斑质心算法[J].光电工程,2006,33(2):41-44
[4]Pasetti A,Habine S,Creasey R.Dynamical binning for high angular rate star tracking[C].The 4thESA International Conference on Spacecraft Guidance,Navigation and Control Systems,Netherlands,Oct 1999
[5]刘金国,李杰,郝志航.APS星敏感器探测灵敏度研究[J].光学精密工程,2006,14(4):553-557
Analysis of Star Image Centroid Accuracy of an APS Star Sensor in Rotation
LI Xiao1,ZHAO Hong2
(1.Beijing Institute of Control Engineering,Beijing 100190,China;2.China Academy of Space Technology,Beijing 100094,China)
Most studies of star image location of star sensors are limited in static state conditions at present.However,the star spot is moving during exposure as a result of satellite rotation,thus influencing the location accuracy of the star image center.In this paper,the accuracy of star image center location in dynamic state is analyzed for active pixel sensor(APS)based star sensors.First of all,sources of the location errors produced by the centroid algorithm are analyzed,a dynamic accuracy estimation method is proposed,and corresponding formulas are deduced.Then choice of the calculation window and the exposure time influencing the dynamic accuracy is analyzed based on given APS star sensor parameters.Finally,corresponding simulations are made to validate the conclusions.
dynamic accuracy;star image center;APS-based star senor;centroid algorithm
V448.22
A
1674-1579(2009)04-0011-06

2008-09-12
李晓(1984—),男,河北人,硕士研究生,研究方向为航天器姿态测量 (e-mail:lixiao789@hotmail.com).

