基于序列二次规划的推力矢量控制分配方法
李 森,胡 军
(1.北京控制工程研究所,北京100190;2.空间智能控制技术国家级重点实验室,北京100190)
基于序列二次规划的推力矢量控制分配方法
李 森1,2,胡 军1
(1.北京控制工程研究所,北京100190;2.空间智能控制技术国家级重点实验室,北京100190)
针对使用推力矢量控制的航天器,建立了游动发动机的数学模型,在分析了游动发动机摆角约束的基础上,提出了推力矢量控制分配问题.将该控制分配问题转化成以力矩误差最小和对变轨推力影响最小作为优化目标的多目标优化问题,引入序列二次规划进行求解,得到一种新的控制分配方法.仿真结果表明,该方法能够准确实现期望目标,验证了所提出的控制分配方法的可行性和有效性.
推力矢量控制;控制分配;游动发动机;序列二次规划
游动发动机作为一种先进的执行机构,在飞船、空间站等航天器上有着很好的应用前景.例如,空间站在完成了与飞船的对接后,质心会发生比较大的变化,当空间站进行变轨时,若使用常规发动机,由于其喷管方向固定,使得所产生的推力方向难以通过空间站质心,对姿态产生扰动力矩,因此必须使用大量的姿控发动机来保持空间站的姿态稳定,而这样就会增加系统的复杂性并增加能耗.如果使用带摇摆喷管的游动发动机,通过调整喷管的摆动角度,一方面可以确保推力方向通过空间站质心,另一方面可以使推力方向偏离质心,产生相对于质心的控制力矩,这样可以利用一组发动机同时对轨道和姿态进行控制.目前,国外已经广泛开展了对基于游动发动机的航天器控制策略的研究,如美国已经在航天飞机[1]和卡西尼号土星探测器[2]上将游动发动机作为执行机构进行在轨试验,取得了良好的效果.
关于控制分配方法的研究,国内外已经取得了很多的成果,其方法可归纳为两类:非优化的控制分配法和优化的控制分配法.非优化的控制分配方法分为直接分配(direct allocation)法、广义逆(pseudo inverse)法和黛西链(daisy chaining)法[3].优化的控制分配方法主要指数学规划方法,又可根据优化目标和约束的特性分为线性规划和非线性规划.非优化的控制分配方法计算量小、易于实现,但是没有充分利用执行机构的控制效率,有较大的保守性.数学规划方法则可以较好地提高执行机构的控制效率,并且可以将摇摆喷管的位置约束和速率约束考虑到规划中去,在两个或者多个游动发动机之间合理的分配控制指令,其缺点是计算量较大,实时性略差,影响了在工程上的应用.不过随着计算机技术的不断发展,数学规划方法具有较好的应用前景[4-6].
本文研究采用双摇摆喷管作为执行机构的控制分配问题.针对该问题,采用文献[7]中提出的多目标优化方法,但由于游动发动机的摆角约束存在非线性因素,使用线性优化方法无法获得解析解,因此本文引入序列二次规划算法(SQP,sequential quadratic programming)对该非线性优化问题进行处理,得到一种新的控制分配方法,该方法能够获得满意的分配结果,准确得到期望力矩,仿真以变轨期间的姿态稳定控制为背景,验证了控制分配方法的有效性.
1 游动发动机模型
1.1 航天器的姿态动力学模型
将航天器简化为刚体,其姿态动力学模型为
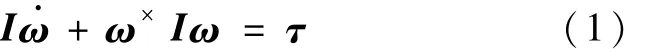
式中,ω=[ ωxωyωz]T是航天器本体相对惯性空间的角速度,I是卫星本体的转动惯量,τ=[ τxτyτz]T为控制力矩,ω×∈R 3×3表示由向量ω张成的叉乘反对称矩阵.
1.2 游动发动机安装模型
由于单台游动发动机难以产生滚动通道的力矩,所以考虑如图1所示的双游动发动机安装方式.Tl、Tr分别为左右游动发动机,其喷管可以在水平和垂直面上摆动,这样在3个通道上均能产生控制力矩.
两台游动发动机相对航天器质心的安装位置分别为

喷管转动角度的定义如图2所示,α,β是摆动喷管转动的角度,X、Y、Z为航天器本体系坐标轴,h是推力矢量.两台发动机产生的推力矢量分别是h1、h2,假定本文中使用的游动发动机其推力矢量的模值是常值,设为 F,有‖h1‖ =‖h2‖ =F.
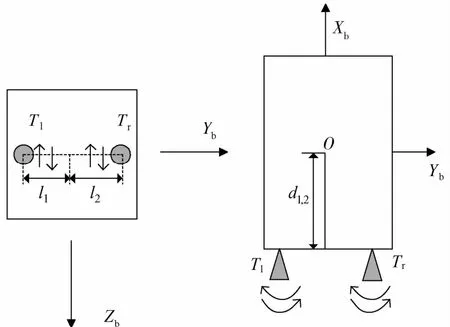
图1 游动发动机的安装示意图

图2 喷管转动角度示意图
根据图1和图2,可以得到

式中,hi1、hi2、hi3(i=1,2)是左右两个喷管产生的推力矢量在本体系3个轴上的分量.
游动发动机产生的控制力矩与喷管摆动角度以及安装位置的关系如下:


综上,本文所考虑的带约束的控制分配问题如下:
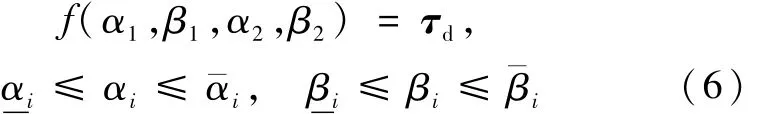
式中,τd是由控制器得到的期望力矩,两个喷管在水平方向和垂直方向的转动角度分别为 αi,βi(i=1,2).由式(2)可知,如果求得推力矢量 h,就能得到喷管的转动角度 αi,βi,所以式(6)可以转化为如下的控制分配问题:
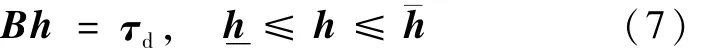
为获得期望力矩 τd,在满足约束条件下,先求得两个发动机的推力矢量,然后根据式(2)求解摇摆喷管的转动角度指令 αi,βi.
2 控制分配方法
控制分配方法要成功地应用到航天器姿态控制系统当中,不仅要解决理论设计上的问题,比如小的控制分配误差,小的能量损失等,还必须考虑工程中的分配实时性问题,将问题的多种限制因素联系起来,综合设计合适的控制分配策略.
本文中提出的控制分配问题的性能指标如下.
a)误差最小化.给定矩阵B,在约束中寻找向量u,使指标 J=‖Bu-τd‖最小.
b)对变轨推力影响的最小化.给定向量 up,在约束中寻找向量u,使指标J=‖u-up‖最小.
c)多目标优化.给定矩阵B、向量 up、加权阵 Q和W,在约束中寻找向量 u满足指标 J=(Buτd)T Q(Bu-τd)+(u-u p)T W(u-u p)最小.
本文中的控制分配问题可以写成如下形式:

的要求来调整加权阵的大小;J中第1项是期望力矩和实际执行机构产生的力矩之间的误差的惩罚项,该惩罚项的引入可以保证在任何条件下规划问题都有解;第2项是喷管转动时实际产生的推力矢量和发动机标称情况下推力矢量差值的模值,代表了对变轨推力的影响.
由凸规划的定义可以看出上述规划问题是非线性且是非凸的,优化目标函数和第1项约束函数是凸的,非凸性主要来自后两项非线性等式约束.这里引入序列二次规划算法来解决此非线性规划问题.
3 序列二次规划算法原理
序列二次规划算法通过求解一系列的二次规划子问题来获得原问题的最优解,因其具有非线性处理能力和超线性收敛速度,因此已经广泛应用于与优化有关的许多领域.由于序列二次规划算法迭代次数少、沿约束边界进行搜索的能力强,所以本文选择用它来求解游动发动机喷管角度的最优化分配问题.
同时含有等式和不等式约束的非线性规划问题(NLP,nonlinear programming)的表达形式如下:

式中:x=(x1,x2,…,xn)T∈R n;f(x)、ci(x)(i∈I)、cj(x)(j∈J)是关于变量 x的函数.
定义 1.设 f(x)、ci(x)、cj(x)可微分,▽f(x)=是NLP的一个局部最小点,且 x*为正则点,则存在拉格朗日乘子 λ*i(i∈I)、μ*j(j∈J),使得成立,这组条件就称为Kuhn-Tucker条件.
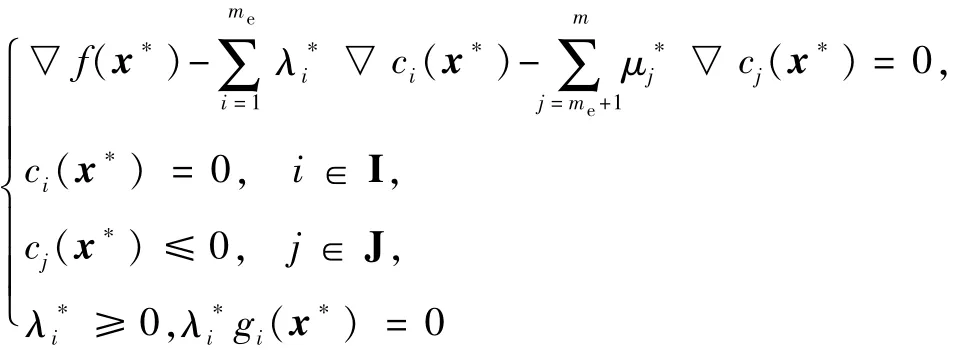
Kuhn-Tucker条件适用于含有等式约束和不等式约束的一般非线性规划问题,是确定某点为NLP全局最优解的必要条件.
NLP的拉格朗日函数为
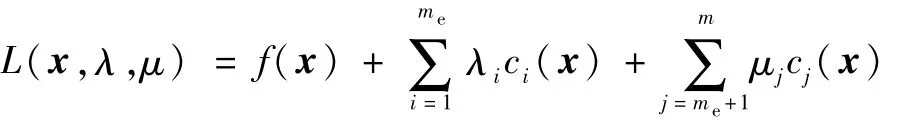
拉格朗日函数的Hesse矩阵计算公式如下:

式中,

含有约束的二次规划问题如下式:

序列二次规划算法在每次迭代中,用近似原非线性规划问题的二次规划子问题来求解搜索方向,具体算法流程如下.
1)给定初值 xk,Bk,k=0.
2)求解式(12)所描述的二次规划子问题,确定搜索方向dk.
3)令 xk+1=xk+dk,判断 xk+1是否满足收敛条件.若满足,则取原问题的解为 x*=xk+1,停止计算;否则将k值加1,返回2)继续迭代.
4 仿真实例
为验证文中提出的控制分配方法的有效性,以刚性航天器为对象,考虑航天器在变轨期间出现了小角度的姿态偏差,为了消除此偏差,以游动发动机为执行机构,将控制律和控制分配方法分开设计,控制律采用最优控制方法设计控制器,仿真参数具体如下:
轨道角速度 ω0=7.27×10-5(°)/s;本体惯量矩阵 I=diag{ 36 971,563 538,577 951} kg·m2;初始姿态[-5° -5° -5°];目标函数加权阵 Q=diag{ 100,100,100},W =diag{ 5 ,5,5};喷管摇摆角度约束 -15°≤α1,2≤15°,-15°≤β1,2≤15°;序列二次规划算法迭代初值 α1,2=0,β1,2=0;游动发动机在标称情况下的推力hp=[490 0 0]T.
选取期望力矩 τd=[100 100 50]TN·m,使用序列二次规划算法分配喷管转动角度,结果如图3所示,经过10步迭代,就可收敛至期望的结果,误差也很小,可见该算法快速、准确,可以满足控制系统实时性的要求.

图3 SQP算法的迭代结果
图4 是将本文设计的控制分配器加入到姿态控制回路之后得到的航天器姿态角变化曲线,可以看出采用非线性控制分配的最优控制方法可以得到良好的控制效果.图5为推力矢量发动机实际产生的控制力矩和期望控制力矩的误差,其绝对量级很小,工程上可以忽略,说明文中使用的基于序列二次规划算法的控制分配方法有比较满意的效果.图6为两台游动发动机转动角度指令,可以看出转动的角度不超过±4°,在游动发动机转动角度约束范围之内,没有超出游动发动机的控制能力范围.图7为3轴的实际推力和标称推力的差值.

图4 3轴姿态角变化曲线
保持Q阵不变,增大W权值,可以降低对变轨推力的影响,仿真结果如图8和图9所示,这时系统的性能有所下降,存在少量的超调,调节时间也更长一些,实际控制量和期望控制量之间的误差也有所增大.经过多次仿真,在系统性能和对变轨推力的影响之间取得了一个平衡,最后选取

图5 实际力矩和期望控制力矩的误差

图6 游动发动机的转动角度

图7 3轴的实际推力和标称推力的差值

通过仿真可以看出,使用游动发动机可以解决航天器变轨期间的姿控问题.经过计算,在小角度机动时对变轨的影响要小于J2项,而且其持续时间不长,所以对变轨的影响也不大.

图8 提高W权值后的姿态角变化曲线

图9 提高W权值后3轴实际推力与标称推力的差值
5 结 论
本文针对使用游动发动机作为执行机构的航天器,研究了基于SQP算法的非线性控制分配方法,通过仿真验证了该方法的有效性,该方法有如下的优点:
1)利用序列二次规划算法处理非线性控制分配问题,其算法成熟,收敛性好,具有较好的解析特性;
2)控制分配方法不受控制律设计的影响,只关心如何将通过控制律所得到的控制量在一定的优化指标下分配给控制面,当航天器结构或发动机的特性发生变化的时候,只需控制分配器重新分配游动发动机转动角度,这样既能保证对控制性能的要求,也简化了控制律的设计,具有实际工程意义.
[1]Enright F J.Thrust vector control algorithm design for the Cassini spacecraft[C].AIAA/AHS/ASEE Aerospace Design Conference,Irvine,USA,February 16-19,1993
[2]Marco B Q,Edward M,Jerry K L,et al.Thrust vector control of the Jovian Icy Moons Orbiter spacecraft[C].The 15thAAS Space Flight Mechanics Meeting,Chicago,USA,June 28-30,2007
[3]Durham W C.Constrained control allocation:threemoment problem[J].Journal of Guidance,Control and Dynamics,1994,17(2):217-221
[4]Pablo A S,Ricardo S P.Spacecraft thruster control allocation problems [J].IEEE Transactions on Automatic Control,2005,50(2):245-249
[5]Tor A J,Thor I F,Svein P B.Constrained nonlinear control allocation with singularity avoidance using sequential quadratic programming [J].IEEE Transactions on Control Systems Technology,2004,12(1):211-216
[6]占正勇,刘林.多操纵面先进布局飞机控制技术研究[J].飞行力学,2006,24(1):13-16
[7]何坚勇.最优化方法[M].北京:清华大学出版社,2007:246-414
[8]袁亚湘.非线性规划数值方法[M].上海:上海科学技术出版社,1993:200-227
Sequential Quadratic Programming-Based Thrust Vector Control Allocation
LI Sen1,2,HU Jun1
(1.Beijing Institute of Control Engineering,Beijing 100190,China;2.National Laboratory of Space Intelligent Control,Beijing 100190,China)
This paper establishes the model of vernier thrusters for spacecrafts using thrust vector control.The thrust vector control allocation algorithm is proposed based on the analysis of the constraints of vernier thrusters.The sequential quadratic programming-based thrust vector control allocation algorithm can minimize the torque errors and thrust errors.Numerical simulation shows that this method can be used to obtain preferable allocation results and the control allocation method is feasible and effective.
thrust vector control;control allocation;vernier thruster;sequential quadratic programming
V448.2
A
1674-1579(2009)04-0017-05

2009-03-18
李 森(1983—),男,河南人,硕士研究生,研究方向为航天器姿态控制技术(e-mail:badlisen@gmail.com).

