空间非合作目标的相对导航粒子滤波算法*

金煌煌，温奇咏，夏红伟，王常虹

（哈尔滨工业大学控制工程系，哈尔滨150001）

空间非合作目标的相对导航粒子滤波算法*

金煌煌，温奇咏，夏红伟，王常虹

（哈尔滨工业大学控制工程系，哈尔滨150001）

针对激光交会雷达作为在空间交会对接过程中的相对导航敏感器，研究了未来特殊背景下，非合作目标航天器对雷达信号发射干扰的情况下的相对导航滤波算法.针对高维模型计算量大的特点对传统粒子滤波算法进行了改进，并与扩展卡尔曼滤波器进行了仿真比较，仿真结果表明改进后的粒子滤波器的滤波效果远远优于扩展卡尔曼滤波器，且计算量优于传统粒子滤波.

非合作目标；自主相对导航；粒子滤波；激光雷达

针对空间合作目标的交会对接技术研究已经进入了实际应用阶段，包括空间站的组建、航天飞机与空间站对接等，诸如美国的阿波罗计划、美国的“阿特兰蒂斯”号航天飞机与“和平”号空间站的对接等交会对接计划的成功实施也标志了交会对接过程中的相对导航逐渐由有人参与到自主导航过渡.

随着人类对空间的不断探索和深入，对航天技术提出了更高的要求.交会对接技术的应用也逐渐由空间合作目标推广到空间非合作目标.空间非合作目标包括故障或失效卫星、空间垃圾等.在追踪航天器对非合作目标的交会对接、捕捉过程中需要得到准确的相对距离、相对速度等信息.针对非合作目标的精确相对导航存在以下可能的困难：观测量不完备、缺少相对定位标志、敌对目标发射的雷达干扰等，因此近年来针对空间非合作目标的相对导航问题已经成为一个研究的热点［1］.

本文研究了在非合作目标对激光交会雷达的观测进行干扰下的滤波问题.将干扰视为非高斯噪声，此时已经无法满足传统的卡尔曼滤波器关于系统噪声和观测噪声都服从高斯分布的假设，且相对导航中的状态方程和观测方程都为非线性，因此需要寻找一种合适的滤波方法.近年来兴起的粒子滤波正是解决非线性非高斯背景下的状态估计的近似最优方法［2］.其基本思想是用一组带权值的离散采样值去逼近一种分布，这些采样值类似于一个个“粒子”，然后在观测的基础上通过调节样本的权值大小和样本位置来获得服从实际分布的样本，并以最终样本的均值为系统状态估计值［3］.但由于传统粒子滤波存在计算量过大的问题，使其很难在实际项目中得到应用，本文将采用一种改进的高斯粒子滤波器，对近地圆轨道上的非合作目标相对导航进行仿真，并通过与传统粒子滤波器以及扩展卡尔曼滤波器的滤波效果进行比较，证明本方法的有效性.

1 相对导航状态方程

记追踪航天器为 c，目标航天器为 t.假设 c在近圆轨道上运动，取目标航天器的轨道坐标系txyz作为相对运动坐标系，其原点与t的质心固连并随其沿轨道运动，x轴与目标航天器的地心矢量重合，由地心指向 t，y轴在追踪航天器的轨道面内垂直于 x轴，并指向运动方向，z轴由右手规则确定，亦即z轴与追踪航天器轨道动量矩矢量的方向一致.轨道坐标系 t－xyz与地心惯性坐标系 OEXYZ的关系如图1所示.

图1 相对运动坐标系与地心惯性坐标系的关系

在地心惯性坐标系中，目标航天器和追踪航天器的动力学方程分别如下：

上式可进一步表示为下列两个等效的关系式

为了建立追踪航天器与目标航天器在动坐标系t－xyz中的相对运动方程，有

将式（5）代入式（7）可得

对于目标航天器和追踪航天器的近距离相对运动情况，航天器间距是小量，特别是当相对高度不大（即 rt／rc接近 1）时.从式（6）可以看出，其右端第一项为中心引力加速度差表达式，通过取一次近似可以进行简化，可得与式（8）比较可知，通过简化将相对运动动力学方程转化为一组常系数线性微分方程［4］.

2 观测模型及非高斯观测噪声建模

利用星载激光雷达可以测量航天器的相对距离ρ和目标航天器相对追踪航天器的方位角α以及俯仰角β，一般可以假设传感器坐标系和追踪航天器轨道坐标系重合，同时基于上述假设可以认为追踪航天器轨道坐标系和目标航天器轨道坐标系平行，基于这两个前提假设可以省略坐标系转换过程.于是在目标航天器轨道坐标系中可以建立观测方程［5］y＝h（x）＋v，其中观测量 y＝（ρ，α，β），h（x）可由下式表示：

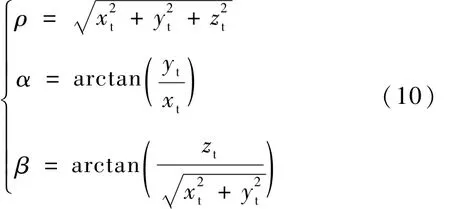
v代表观测噪声采用的闪烁分布.考虑到非合作相对导航过程中传感器观测量可能受到的非合作干扰，假设观测噪声为角闪烁噪声，角闪烁是光学区跟踪雷达在近距离上面临的主要误差源，其产生机理与扩展目标的散射中心理论密切联系.在光学区，目标可以看作由许多散射中心组成，目标回波可以看作由这些散射中心的回波反射合成的，合成结果等效为一个视在中心，这个中心的位置也就是实际测得的位置.随着目标航天器和追踪航天器间的相对运动，散射中心的反射也在不断变化，导致视在中心发生变化，从而产生测角误差，这种现象称为角闪烁，严重时角闪烁可以导致跟踪点偏离到目标之外［6］，闪烁噪声的概率密度函数为

式中，ε为一小于1的正数，pG（w）为高斯密度函数，pt（w）表示厚尾分布，常用的厚尾分布有拉普拉斯分布、t分布、均匀分布、大方差的高斯分布等，选取pt（w）为拉普拉斯分布.

3 粒子滤波算法

针对模型中存在的非线性以及非高斯噪声干扰，需要选取合适的滤波算法.粒子滤波算法是一种基于蒙特卡罗仿真的近似贝叶斯滤波算法.它的核心思想为用一批有相应权重的离散随机采样点来近似状态变量的后验概率密度函数（pdf），这批采样点被称为粒子，并根据这些粒子以及它们的权重来计算估计值.当粒子数很多的时候这种滤波方法就可以接近最优贝叶斯估计.状态变量的概率密度函数提供了有关状态变量分布的所有信息，一旦获得了概率密度函数，就可以依照不同的准则函数计算得到状态变量的极大似然估计、最小方差估计、最大后验估计等等.相对于EKF和UKF算法，粒子滤波算法能够处理任意的非线性函数和非高斯分布，根据采样点就能够得到均值、协方差和其他统计量.

基本粒子滤波算法基于Gordan等人在20世纪90年代提出的“采样-重要性-重采样”（SIR，sampling importance resampling）滤波算法［7］，与其他粒子滤波算法而言，它具有简单和易于实现的特点.下面简要介绍一下贝叶斯估计理论和SIR算法.

3.1 贝叶斯估计理论

假设一般非线性动力学系统的状态方程和测量方程分别为

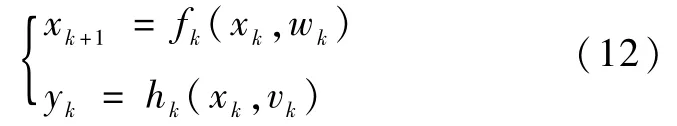
贝叶斯估计的目标是构建状态变量的后验概率密度函数 p（xk＋1｜Yk＋1）.为此有贝叶斯递推滤波算法，该算法每一步递推过程由预测和更新两步组成［8］.

预测：当已知 k时刻的概率密度函数 p（xk｜Yk）时，利用给定的系统状态方程（12）与过程噪声的统计特性 p（wk），可以预测状态的前验概率密度p（xk＋1｜Yk），具体算式为

更新：当k＋1时刻的测量 yk＋1获得时，则可利用系统的测量值、测量模型及测量噪声统计特性，对前验概率密度函数p（xk＋1｜Yk）进行修正并给出后验概率密度 p（xk＋1｜Yk＋1），具体算式为

以上为严格的贝叶斯滤波公式，对于线性高斯系统，pdf可由均值和方差来表示，状态的最小方差估计可以由卡尔曼滤波得到，而对于非线性、非高斯系统，则无法求得上述概率密度函数的解析解.为此需要寻找适于更多实际系统应用的状态概率密度函数的近似求解法.其中粒子滤波则为一种有效的近似方法.

3.2 SIR粒子滤波方法

根据蒙特卡罗近似方法，后验概率密度函数p（xk｜Yk）可由一批离散的采样点｛，｝近似，i＝1，…，N，其中称为粒子，为相应的权值

＝1.下标k代表时间，于是k时刻的后验概率密度可以离散的加权近似为

其中权值可以通过重要性采样法进行选择.如果能直接从p（x）中产生粒子，则每一粒子将被赋予1／Ns的权值.当无法直接从 p（x）中产生粒子时，选择从分布 q（x）中产生粒子，这里 q（x）称为重要性函数.这样，可以根据下式分配权值重要性函数在粒子滤波器的性能中起着关键的作用.一般的，q（x）越接近于 p（x）越好.最常用的两个重要性函数是先验重要性密度函数与最佳重要性密度函数.先验密度函数取为p（xk），基于更新表达式（14），它意味着权值的更新为而最佳重要性函数取为p（xk，y0：k），权值更新则依据

可见，实现先验重要性密度函数比较容易，因为选最佳重要性函数时计算－）需要积分.顺序的重要性采样任务就是从重要性函数中采样生成样本集和递归地计算重要性权重.

然而，随着迭代次数的增加，重要性权值的分布变得越来越倾斜，这就是粒子滤波容易出现的粒子退化现象，即除了一个粒子外，所有粒子只具有微小的权值［9］.为了避免粒子退化，Gordan等人提出了重采样方法，其主要思想是去除那些权值小的粒子，复制权值大的粒子.

基本SIR粒子滤波算法步骤参见参考文献［3］.

3.3 高斯粒子滤波

传统的基本SIR粒子滤波存在计算量大、权值退化以及多样性匮乏等缺点，很难在实时性要求很高的自主相对导航中得到实际应用，针对以上缺点，一些改进的粒子滤波算法层出不穷.为了获得更好的重要性密度函数，先后提出了辅助粒子滤波算法（auxiliary particle filter）；扩展卡尔曼粒子滤波算法（extended Kalman particle filter）等一系列有效的方法.为了解决重采样步骤带来的粒子多样性匮乏问题，又进一步在粒子滤波中引入了马尔可夫链蒙特卡洛移动 （MCMC，Markov chain monto carlo）步骤［10］.

本文应用了一种新的滤波器即高斯粒子滤波器［11］.该滤波器基于粒子滤波方法得到一高斯分布来近似估计未知状态变量的后验分布.并通过仿真结果表明，该滤波器滤波精度高于 EKF，并且由于该滤波器将后验分布近似成高斯分布，因此不需要重采样，也不需要重采样，不存在粒子退化现象，极大的降低了粒子滤波的复杂性和计算量.高斯粒子滤波的基本思想是通过一个高斯分布近似滤波概率分布，具体的高斯粒子滤波算法步骤［12］如下：

1）判断是否是初始化步骤，若是则根据初始化方法从 p（x0）采样粒子，若不是则根据 N（，Pk－1）采样得 N个粒子（i＝1，…，N）；

3）输出：

4）判断滤波是否结束，若没结束则返回到1）.

4 仿真实例

4.1 状态方程离散化

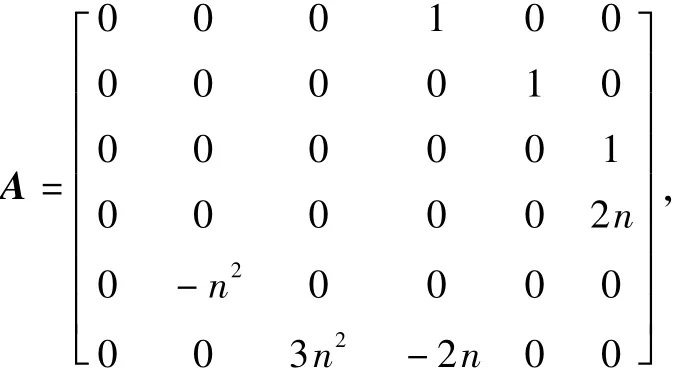
离散化后的状态方程为

X（k）＝ΦX（k－1）＋Γw（k），

式中T为采样周期，s和c分别代表sinωT和cosωT.Γ为过程噪声方差阵，

式中w（k）为系统过程噪声，在仿真中假设为高斯白噪声.

4.2 仿真结果与分析

为了验证方法的有效性，本文进行了仿真试验，仿真条件如下：目标航天器的轨道参数取为：轨道高度为780 km圆轨道，激光雷达的测距精度为0.6 m（3σ），对视线角的测量精度为 0.1°（3σ）；相对轨道状态初始条件如下：X0＝［－520，10，20，－0.0324，－0.02，0.02］T，滤波器初始条件为X＾0＝［－510，0，1，0，0，0，0］T；采样周期为 1 s.

对EKF、PF和 GPF三种滤波器进行了仿真比较，PF和GPF粒子数为1 000时运行100个周期的误差曲线如图2～图4所示.

图2 x轴相对距离误差曲线

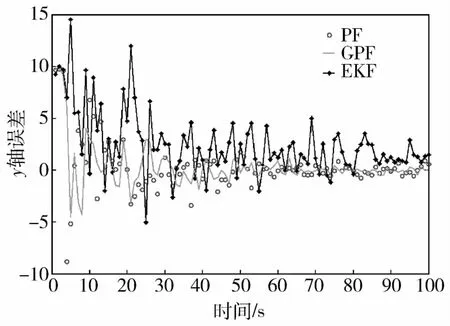
图3 y轴相对距离误差曲线

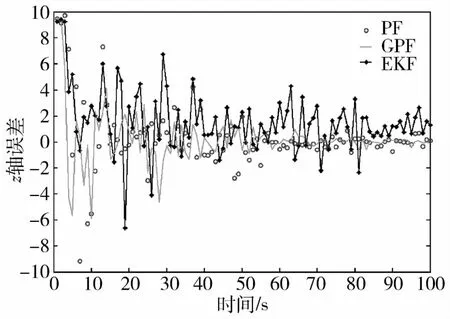
图4 z轴相对距离误差曲线

表1 GPF（粒子数 N＝1 000）与 PF、EKF的性能对比

从图2～图4以及表1可以看出，对非线性系统存在非高斯噪声干扰的情况下，GPF比EKF更快速地逼近到真值，最终的误差值也收敛到允许范围内；并且在高维模型的背景下，GPF比基本粒子滤波实时性要好得多，能基本符合实际应用的要求，从粒子滤波的粒子权重更新值上也证明了GPF不存在粒子退化现象，从而不需要重采样步骤，大大节省了计算量.

5 结束语

本文应用一种改进的粒子滤波算法——高斯粒子滤波（GPF），解决了基本粒子滤波在处理高维模型时的计算量大、粒子多样性匮乏等问题，而且处理非高斯噪声的能力优于EKF，具有重要的应用前景和进一步研究价值.

［1］张秋华，韩琦，孙毅.空间非合作目标交会运动状态估计的卡尔曼滤波方法［A］.全国测控、计量与仪器仪表学术年会论文集（下册），2004

［2］李保国，肖怀铁，王远模，等.角闪烁背景下基于粒子滤波器的跟踪研究［J］.现代雷达，2006，28（2）：54-55

［3］胡士强，敬忠良.粒子滤波算法综述［J］.控制与决策，2005，20（4）：361-365

［4］郗晓宁，王威，高玉东.近地航天器轨道基础［M］.长沙：国防科技大学出版社，2003：244-247

［5］何英姿，谌颖，韩冬.基于交会雷达测量的相对导航滤波器［J］.航天控制，2004，22（6）：17－20

［6］刘勇，徐世杰.航天器相对轨道自主确定算法研究［C］.全国第十二届空间及运动体控制技术年会，桂林，2007

［7］黄培康.雷达目标特征信号［M］.北京：宇航出版社，1993

［8］Gordan N J，Salmond D J.Novel approach to nonlinear and non-gaussian bayesian state estimation［J］.Proc.of Institute Electric Engineering，1993，140（2）：107-113

［9］Arulampalam M S，Maskell S，Gordan N，et al.A tutorial on particle filters for online nonlinear non-Gaussian Bayesian tracking［J］.IEEE Transactions on Signal Processing，2002，50（2）：174-175

［10］胡洪涛，敬忠良，李安平，等.非高斯条件下基于粒子滤波的目标跟踪［J］.上海交通大学学报，2004，38（12）：1998

［11］戴丁樟.粒子滤波算法研究及其在目标跟踪中的应用［D］.哈尔滨工业大学，2006，11：32-33

［12］王宁，王从庆.高斯粒子滤波器及其在非线性估计中的应用［J］.南京航空航天大学学报，2006，38（增刊 1）：132-135

［13］Kotecha J H，Djuric P M.Gaussian particle filtering［J］.IEEE Transactions on Signal Processing，2003，51（10）：2592-2601

Particle Filter Algorithm for Relative Navigation of Space Non-Cooperative Target

JIN Huanghuang，WEN Qiyong，XIA Hongwei，WANG Changhong
（Dept.Control Engineering，Harbin Institute of Technology，Harbin 150001，China）

Taking a laser radar as the relative navigation sensor during space rendezvous and docking in space，a relative navigation filter algorithm for a non-cooperative target spacecraft eradiating radar jamming signal is investigated for a special situation in the future.Considering large computational effort for high-dimensional model，traditional particle filter algorithm is improved，and compared with EKF through simulation.The simulation results show that the filtering effect of improved particle filter is much better than the EKF，and the computational effort is largely reduced compared with traditional particle filter.

non-cooperative target；autonomous relative navigation；particle filter；laser radar

V4

A

1674-1579（2009）04-0006-05

*黑龙江省青年科学技术专项资金（QC07C15）资助项目.

2009-03-15

金煌煌（1986—），男，安徽人，硕士研究生，研究方向为空间相对导航 （e-mail：jinhh10＠gmail.com）.