平流层飞艇巡航姿态自适应神经网络补偿控制*
刘其睿,李 勇
(1.北京控制工程研究所,北京100190;2.空间智能控制技术国家级重点实验室,北京100190;3.中国空间技术研究院研究发展中心,北京100094)
平流层飞艇巡航姿态自适应神经网络补偿控制*
刘其睿1,2,李 勇3
(1.北京控制工程研究所,北京100190;2.空间智能控制技术国家级重点实验室,北京100190;3.中国空间技术研究院研究发展中心,北京100094)
研究了一种基于自适应神经网络补偿的平流层飞艇前向速度与姿态控制系统设计方法.针对近似模型进行常规线性动态补偿器设计,并引入自适应径向基函数(RBF,radial basis function)神经网络对模型误差进行补偿.根据Lyapunov方法得到神经网络权值自适应律,保证了闭环系统误差信号一致最终有界.仿真结果表明对于两类不同的飞艇模型,所设计的控制器在响应性及对未知环境风速作用的鲁棒性方面均具有良好的效果.
平流层飞艇;巡航姿态;神经网络;自适应
平流层飞艇是工作在平流层中下层(20~40 km)的可控浮空器,因其可作为执行高空长航时应用任务的平台,近年来成为了全球范围的研究热点.实现平流层飞艇自主运行的关键就是要解决其自主综合控制问题[1],巡航控制问题是其中的一个重要方面.
由于平流层飞艇动力学模型具有非线性、多变量及参数慢时变等特点,经典的线性控制理论难以解决其控制问题,目前的研究文献多集中于动态逆、反步法、滑模控制等先进控制方法领域[2].文献[3]将线性矩阵不等式(LMI,linear matrix inequality)方法应用于飞艇的鲁棒航向控制系统设计,所得到的控制器对于具有参数不确定性的飞艇模型有着良好的跟踪性能.但控制律的状态反馈形式要求状态量精确已知,另一方面采用固定增益使得控制律具有较大的保守性.
2001年,Calise等人提出了一种基于反馈线性化和自适应神经网络补偿的直接自适应输出反馈控制方法[4],其基本思路是利用径向基函数(RBF)神经网络对非线性动力学函数的逼近能力补偿反馈线性化带来的模型误差,以提高常规线性控制器的鲁棒性,根据Lyapunov方法设计神经网络权值的自适应律,从而保证闭环系统误差信号一致最终有界.本文主要参考这一思路,对平流层飞艇的前向速度与姿态控制系统进行了设计.
1 平流层飞艇的数学描述
目前公开发表的研究文献中,欧阳晋[5]等人给出了较为完整的飞艇参数数据,所建立的飞艇模型采用刚体假设.本文所研究的飞艇模型以文献[5]中所给出的模型为基础.假设飞艇具有对称平面xoz,重心在对称平面内,惯量积 Ixy=Ixz=0.直接取推力 Tthrust和滚动、俯仰、偏航力矩 Mroll、Mpitch、Myaw作为控制量.其六自由度动力学和运动学方程描述如下:
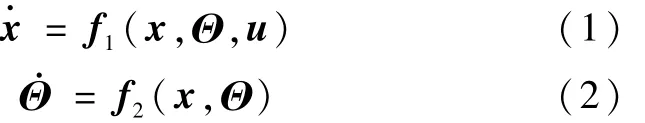
其中式(1)也可写为如下形式:

在上述方程中,f1(·),f2(·)是矩阵形式的函数.状态向量x=[ u v w p q r]T,代表飞艇在本体系的三个线速度分量和三个角速度分量;姿态角向量Θ=[ φ θ ψ]T,代表飞艇本体系相对地面系的三个姿态角分量,详细说明参见参考文献[5].式(1)中的控制量u=[ TthrustMrollMpitchMyaw]T.在式(3)中,Mm为质量矩阵
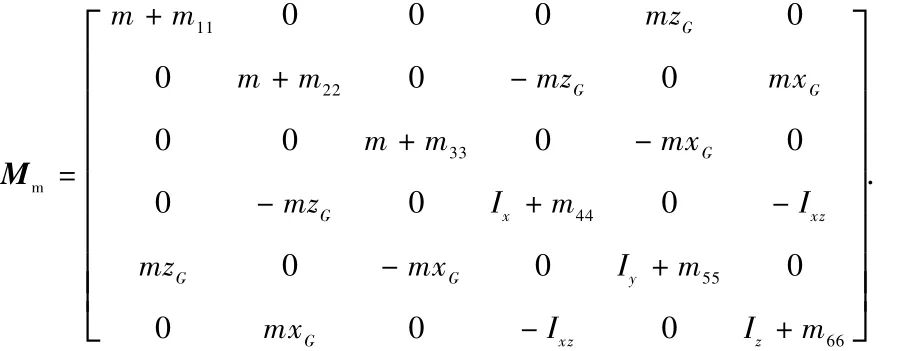
式中,m为飞艇质量,Ix,Iy,Iz,Ixz为飞艇绕 ox,oy,oz轴的转动惯量和绕 xoz平面的惯量积,mii(i=1,2,…,6)为飞艇的流体附加质量,xG,zG是飞艇质心在ox,oz轴的坐标.式(3)右边有流体惯性力项 Df,空气动力项At,重力项G,浮力项B,其具体表达式见参考文献[5],此处不再赘述.式中的控制量 U=[Tthrust0 0 MrollMpitchMyaw]T,仅在形式上与式(1)中的u有区别.f2(·)的形式如下:本文的设计目标为设计控制量u,使得飞艇巡航速度矢量在存在参数不确定和未知风速干扰条件下跟踪期望的巡航速度指令,即使得前向速度u和巡航姿态角Θ分别跟踪前向速度指令uc及姿态角指令

2 基于自适应神经网络补偿的姿态控制器设计
2.1 基于自适应神经网络补偿的控制方法
对于一般的非线性单输入单输出(SISO,singleinput-single-output)系统

式中,x′是 n维状态向量,u′,y′分别是系统输入和输出信号.假设系统满足输出反馈线性化条件并具有相对阶 r[6],即

式中 hr≜drh/d tr,且有∂hi/∂u′=0,0≤i<r及∂hr/∂u′≠0.引入变换


其中 Δ′=Δ′(x′,u′)=hr(x′,u′)-′,u′)可视为扰动信号.此时系统的实际控制输入u′可直接求逆得到

假设系统输出y′要求跟踪已知的参考输入y′c.伪控制信号v′选为如下形式:


图1 基于自适应神经网络补偿的控制设计原理
线性动态补偿器是单输入双输出系统

自适应神经网络的输出


式中ηci是每个神经元的中心值.神经网络的输入η′为
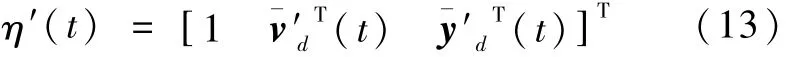
式中,

这里 n1≥n,d>0.
神经网络权值自适应律为

式中,F>0,λw>0是自适应增益.φf是 φ经过低通滤波器 T-1(s)的输出.T(s)是多项式,其设计与线性动态补偿器(10)有关.多项式 Ddc(s),Ndc(s),Nad(s)以及 T(s)需要满足一定的条件[4].
文献[4]的定理2采用 Lyapunov方法证明:在设计参数满足一定的条件下,上述控制器设计能够保证闭环系统的误差信号一致最终有界(关于系统的解一致最终有界的定义见参考文献[11]).
2.2 姿态控制器设计
在本文的姿态控制器设计问题中,以姿态角Θ作为输出量,容易验证系统(1)~(2)满足输出反馈线性化条件,且系统相对阶为2

但函数h2(·)的形式难以直接得到.考虑将式(3)中的 Mm分解为确定项和不确定项 ΔMm,式(2)中的 f2分解为确定项和不确定项 Δf2



注意到经过以上式(17)~(19)的处理,将流体附加质量、流体惯性力、空气动力等项归纳到不确定项中,使得只包含确定项的近似模型无需考虑流体附加质量、空气动力系数等参数的具体数值.而通常这些参数需要数值估算或实验测定,难以得到精确值.在此基础上,原系统模型(1)~(2)可改写为如下形式:

式中,Δu、Δv、Δw及 Δ′是近似模型与实际对象之间的偏差.根据反馈线性化的思想,引入输入变换
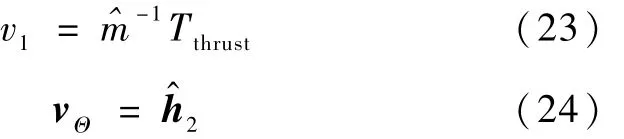
系统模型(1)~(2)转化为

显然实际控制信号 u可由式(23)及(24)逆计算得到.这样原设计问题就转化为伪控制信号 v1及 vΘ的设计问题.
观察式(25)及(26)两组方程,式(25)是一阶系统,其控制设计问题较为简单,这里采用常规的线性动态补偿器设计.式(26)是二阶系统,且与式(25)相比属于快动态,其控制设计较为困难.将式(26)按照滚动、俯仰、偏航通道分解为三个SISO子系统,在每个通道上的统一形式为

于是可以按照图1的标准模型将伪控制信号vs设计为如下形式:

式中,Θsc是Θc在 vs相应通道上的分量,通过二阶滤波器可以很容易的得到.vdc是线性动态补偿器的输出,用于使式(27)在 Δ′s=0时的近似模型稳定.vad是自适应神经网络的输出,用于近似抵消 Δ′s.并按照上一节中的介绍依次进行vdc及vad的设计.
对于v1的设计则较为简单,可按经典方法设计传递函数形式的动态补偿器如下:
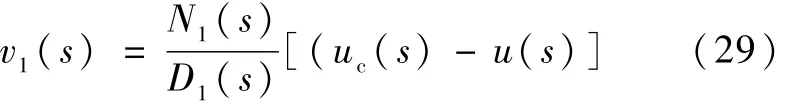
根据文献[4]的定理2,如上所述的控制器设计能够保证闭环系统的误差信号一致最终有界.
3 仿真结果
本文的仿真分别对两类飞艇模型A和B进行验证.飞艇模型A的参数如质量、转动惯量、附加质量和气动参数等数值引自参考文献[5]及文献[10].考虑到飞艇模型A是在近海平面高度飞行的19 m小型验证艇,为验证本控制器设计对平流层飞艇的控制效果,在参考文献[1]所给250 m大艇数据的基础上计算得到飞艇模型B的参数.为考察控制器的抗干扰能力,根据平流层风速特性并不失一般性,在仿真中引入风速模型为地面系X轴方向存在-10 m/s的恒定风速,同时三轴均存在均方差为0.316 m/s的零均值高斯白噪声随机风速.控制器设计参数如下.
滚动、俯仰、偏航通道的线性动态补偿器统一设计为
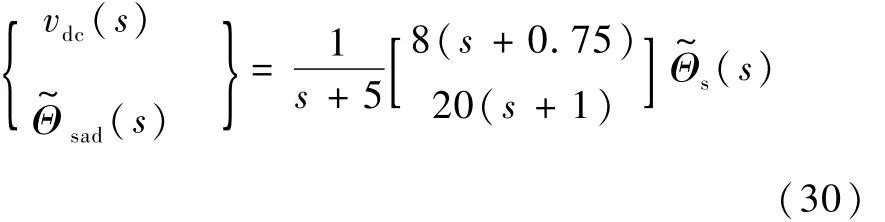
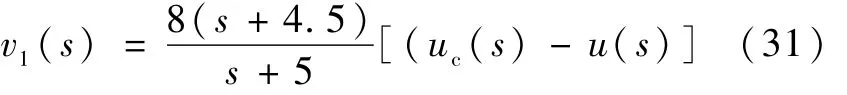
为消除稳态偏差,分别在每个通道增加了PI控制.
飞艇模型A在无风和有风两种情况下的仿真见图2和图3.可见在速度与姿态控制系统的作用下,飞艇能够迅速跟踪参考指令,在无风情况时响应时间在10 s左右,稳态偏差小,并且在存在未知风速时仍能稳定跟踪,表现出良好的机动性与鲁棒性.飞艇模型B在有风扰时的仿真见图4.其控制效果要好于飞艇模型A.

图2 无风扰时的飞艇模型A速度与姿态跟踪性能

图3 有风扰时的飞艇模型A速度与姿态跟踪性能
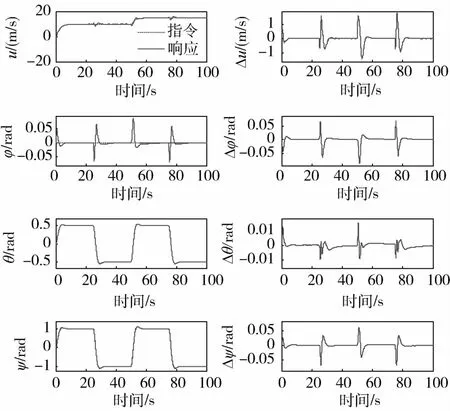
图4 有风扰时的飞艇模型B速度与姿态跟踪性能
4 结 论
本文应用基于自适应神经网络补偿的设计方法,对平流层飞艇的前向速度与姿态控制系统进行了设计.该控制器设计方案对模型参数信息仅有较少的要求.仿真结果表明,对于两类不同的飞艇模型,本文所设计的控制器均具有良好的响应性和对未知的环境风速作用的鲁棒性,控制器设计是有效的和可靠的.
[1]Mueller J B,Paluszek M A,Zhao Y Y.Development of an aerodynamic model and control law design for a high altitude airship[C].AIAA 3rd“Unmanned Unlimited”Technical Conference,Workshop and Exhibit,Chicago,Sep 2004
[2]Paiva E C,Benjovengo F,Bueno S S,et al.Nonlinear control approaches for an autonomous unmanned robotic airship[C].AIAA Aviation Technology,Integration and Operations Conference,Belfast,Northern Ireland,Sep 2007
[3]屈卫东,罗昌行,欧阳晋.无人飞艇的鲁棒航向控制系统设计[J].系统仿真学报,2004,16(11):2575-2579
[4]Calise A J,Hovakimyan N,Idan M.Adaptive output feedback control of nonlinear systems using neural networks[J].Automatica,2001,37(8):1201-1211
[5]欧阳晋.空中无人飞艇的建模与控制方法研究[D].上海交通大学,2003
[6]Isidori A.Nonlinear control systems[M].Berlin:Springer,1995
[7]Kim Y,Lewis F.High level feedback control with neural networks[M].NJ:World Scientific,1998
[8]Ioannu P A,Sun J.Robust adaptive control[M].Englewood Cliffs,NJ:Prentice-Hall,1996
[9]Sanner R,Slotine J.Gaussian networks for direct adaptive control[J].IEEE Transactions on Neural Networks,1992,3(6):837-864
[10]王晓亮,刘丹,单雪雄.飞艇最优飞行轨迹研究[J].力学季刊,2005,26(4):555-561
[11]Khalil H K.Nonlinear systems[M].3rd ed.Upper Saddle River,NJ:Prentice-Hall,2002
Adaptive Neural Network Compensation for Stratospheric Airship Attitude Control of Cruising Phase
LIU Qirui1,2,LI Yong3
(1.Beijing Institute of Control Engineering,Beijing 100190,China;2.National Laboratory of Space Intelligent Control,Beijing 100190,China;3.R&D Center,China Academy of Space Technology,Beijing 100094,China)
By designing a speed and attitude control system based on the adaptive neural network compensation,this paper investigates the cruise tracking control problem for the stratospheric airship.An adaptive RBFNN(radial basis function neural network)is used to compensate modeling errors,which come from the approximate model applied to a regular linear controller design.The network weight adaptation law,derived from the Lyapunov stability analysis,guarantees that the tracking errors are ultimately bounded.Simulation results demonstrate the excellent performance and robustness of the controller,even if environmental winds with unknown information exist.
stratospheric airship;cruise tracking;neural network;adaptive control
V448
A
1674-1579(2009)04-0034-05

*中国空间技术研究院自主研发课题及国家自然科学基金(60804016)资助项目.
2009-03-10
刘其睿(1981—),男,山东人,硕士研究生,研究方向为航天器智能控制 (e-mail:raymann67@163.com).

