基于粒子群算法的绳系卫星展开与回收控制
王 维,李俊峰,宝音贺西
(1.西安卫星测控中心,西安 710043;2.清华大学航天航空学院,北京100084)
基于粒子群算法的绳系卫星展开与回收控制
王 维1,李俊峰2,宝音贺西2
(1.西安卫星测控中心,西安 710043;2.清华大学航天航空学院,北京100084)
绳系卫星的展开与回收是绳系卫星应用的基础问题,但通过改变系绳拉力来实现展开和回收的方法尚未得到充分研究.将系绳拉力作为控制力,并在时间域内离散,然后利用粒子群优化算法在整个可行域中寻找满足优化指标的最优值,从而得到控制力的变化规律.该控制方法可以使绳系卫星系统在最小摆动、最短时间等最优指标意义下,迅速展开到平衡位置,同时也适用于绳系卫星的回收.仿真结果表明:该控制方法同基于控制展开与回收速度的控制方法相比,展开和回收的时间短、侧向摆动小,具有一定优越性.
绳系卫星;展开;回收;粒子群算法;最优指标
绳系卫星系统通常由一个细长的绳索连接起来的两颗卫星组成,两颗卫星以相同的角速度在轨道上运行.绳系卫星的动力学与控制是目前航天应用的热点问题之一,在近地空间应用、深空探测等方面有重要的应用[1].
绳系卫星的展开和回收,一直是绳系卫星动力学研究的基础问题和重点问题.其控制策略,可以分为两种:一是对展开速率的控制[2-3],如绳长以经典的指数—匀速—指数控制方式展开与回收、等速率展开与回收等,这种方法比较直观、简单,但无法控制面内角振动,也无法预知系绳的拉力大小.为了避免拉力过大造成危险,展开速度不能太快;二是通过系绳拉力控制.由于系绳的拉力大小和绳系卫星的展开与回收的关系比较复杂,所以这种控制方法更复杂[4].
文献[5]使用拉力控制绳系卫星的展开,其缺点和未改进的控制展开速率的方法一样[2],在展开到平衡位置后,子星角速度不为0,在平衡位置附近摆动很长时间才能逐渐停止摆动.本文采用粒子群优化算法优化系绳拉力,控制展开和回收.这种控制算法克服了文献[5]控制方法的不足,使子星在到达平衡位置时,角速度也为0.本文的这种优化方法属于直接优化算法,同间接优化算法控制系绳展开相比[6],不需协态变量,在计算上更易于实现.
1 模型的建立与简化
图1为一个典型的绳系卫星示意图.图中绳系卫星系统由主星S1和其子星 S2组成,假设主星的质量远远大于子星,系绳看作刚体,质量忽略不计,在拉力下产生的形变忽略不计.图2为轨道系下的绳系卫星示意图.图中:l为系绳长度;θ为系绳和竖直方向上的夹角,称为面内角;φ为系绳与轨道面的夹角,称为面外角.
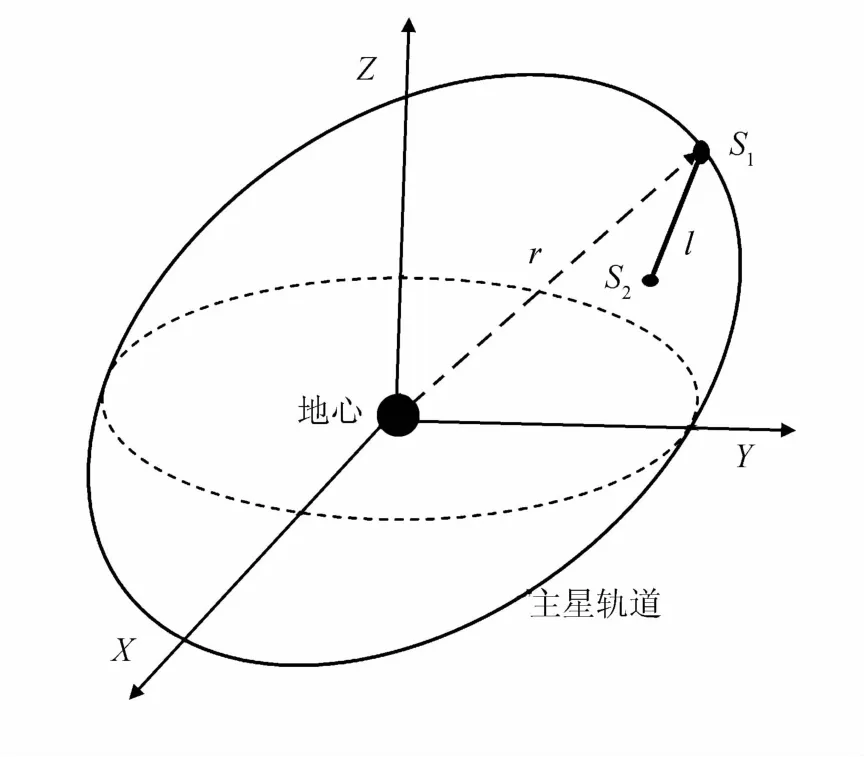
图1 绳系卫星示意图(惯性系)
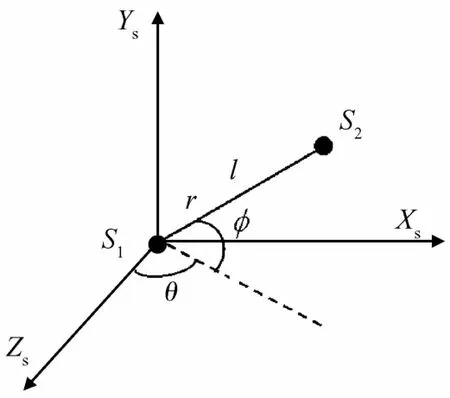
图2 绳系卫星示意图(轨道系)
绳系卫星的面外角φ与长度l和面内角θ的运动是解耦的[5],所以系绳在展开时,系绳长度的变化只影响面内角.本文忽略面外角的变化,考虑二维模型,动能为
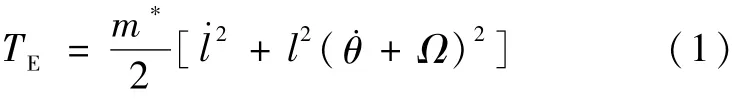
系统的势能为

应用拉格朗日方程
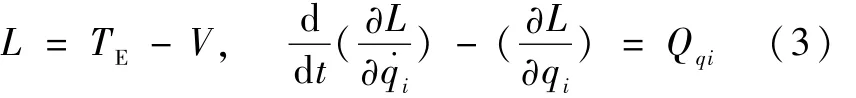
得到系统微分方程

式中Ql为广义力.由系统方程(4)可以看出,系统具有较强的非线性.
绳系卫星的系绳长度一般比较长,能够达到几十千米,但是面内角一般在-π~π内变化.系绳长度和角度的数值在量级上的差别给后面的优化计算带来困难.同时,轨道高度不同,角速度 Ω也不同.为了解决这两个问题,对上面的方程无量纲化,得

2 任务需求与控制方法分析
绳系卫星执行任务时,一般会经历展开、停留、回收3个工作状态.通过控制系绳的拉力,可以展开系绳.展开完成后,通过主星内部的控制机构将系绳卡紧,保持系绳长度不变,就可以实现系绳的停留.而回收的过程与展开过程非常类似,只是初始条件和结束条件不同.
展开后的末端状态绳长 l=lf,θ=0,即展开到指定的位置,同时,要求=0,=0.展开时间 t不能太长、侧向摆动 E尽可能小.系绳拉力 T不能大于拉力限度T*,否则系绳断裂.
通过拉力控制展开,不但可以控制面内角,还不必担心展开过快导致系绳拉断.但系统方程(5)是比较复杂的非线性方程,无法得到拉力T与系绳长度l和面内角θ的解析关系,所以这种方法相对复杂.
通过拉力控制绳系卫星的展开与回收,可看作一个非线性方程的规划问题,本文利用粒子群方法,将其转化成优化问题来解决.优化指标定义为
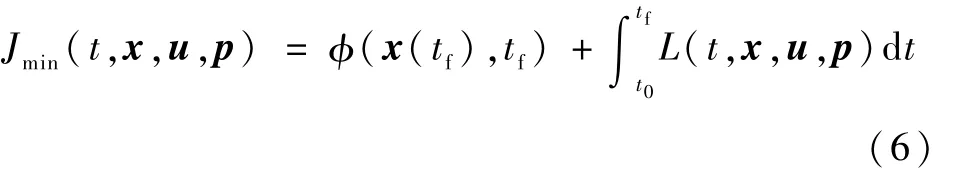
式中,x是状态量,u是控制量,p为扰动量,选定优化指标

式中,Tf指总的展开时间,θ(t)指展开过程中的侧向摆动,下标带有 f的量是指定达到的末端状态,分别表示对展开时间最短、面内角最小(控制侧向摆动)和最终展开的位置、速度的要求,λ1、λ2、λ3是惩罚系数.当优化指标 J取最小值时,认为在满足最短时间、最小摆动的条件下,系绳展开到了指定位置.
将拉力在时间域上等分为10段,作为要优化的变量,并限定在一定范围 (满足T≤T*)内.在每时间段内,选取不同的拉力,则得到不同的结果,这些结果的指标值也不同.为了得到指标的最优值,选用粒子群方法[6]来进行优化.
粒子群算法同遗传算法、蚁群算法、进化算法等全局优化算法一样,都属于生物智能算法.对于问题维数不多的问题,利用粒子群算法可以迅速有效地找到全局最优解.
粒子群算法模拟鸟群的捕食行为,可分为随机初始化、适应值计算比较、变异进化和筛选4步.在第4步中筛选最优粒子并判断是否达到停止条件,如果“是”则停止迭代,否则从第2步重新开始迭代.
粒子群算法的迭代公式为

式中:s和v为当前粒子的位置和位移;s-和 v-表示上一时刻的 s和 v的值;R表示取随机数;c1和c2为常数,取0.5;pb和 gb分别代表目前全局最优适应值和当前种群最优适应值;pr表示当前粒子的适应值.
选择一定规模的种群,经过多次迭代,可以得到一个满足约束且优化指标较好的解.
3 数值仿真与结果比较
用绳系卫星TSS-1飞行任务的数据进行仿真计算,验证算法的有效性.TSS-1执行的飞行任务是NASA与意大利航天局(ASI)合作进行的第1次从航天飞机上释放绳系卫星.航天飞机位于296 km的高度,展开的目标系绳长度为20 km,从航天飞机释放的子星质量为518 kg.用系绳从航天飞机将子星展开,展开到20 km处,停留3 h并执行任务,然后回收到2.4 km处,停留2 h再次执行任务,最后回收到航天飞机上.取粒子群算法的变量个数为11,种群规模为200,终止代数为200.
得到的控制力的变化和子星的路径随时间变化的结果如下:
系绳在41.4 min时间内,可从主星展开到预定位置,此时拉力不断变化,但始终小于70 N.停留3 h后,系绳经过44.1 min收回到2.4 km处,再停留2 h,最后用了26.9 min收回到主星.总过程412.419 4 min.两次停留过程中,保持拉力 T=3m*Ω2l,等于相应长度的重力梯度力,这样可以控制系绳长度不变.图3是展开、回收过程中系绳长度变化示意图,图4是展开、回收过程中系绳拉力的变化示意图.
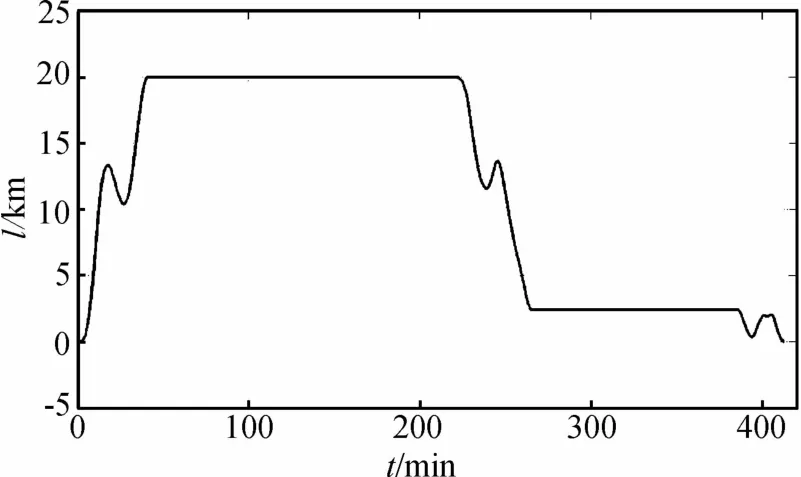
图3 绳长变化示意图

图4 拉力变化示意图
图5 、图6是文献[3]的基于展开、回收速度控制的展开与回收过程,其展开、回收需要数小时,误差量级1 m,展开、回收侧向摆动幅度分别为5.2 km和5.8 km.本文方法的展开、回收时间在1 h以内,长度误差量级0.1 m,侧向摆动幅度为4.5 km和3.9 km,如图7、图8所示.

图5 基于速度控制的系绳长度变化

图6 基于速度控制的系绳拉力变化

图7 展开过程的侧向摆动

图8 回收过程的侧向摆动
文献[2]是使用系绳长度控制展开与回收的仿真结果,其侧向摆动5.8 km和4.5 km,展开与回收的时间需要十几个小时.由此可见,本文的控制方法在展开与回收的时间、位置、速度精度和侧向摆动方面都具有一定优势.
4 结 论
本文将非线性方程的控制问题,转化为一个优化问题,这种方法和具体的模型无关,可以进一步拓展到三维情况,也可以将各种摄动力都加入到系统方程中.同基于展开速度的控制方法相比,该方法的展开速度更快,侧向摆动更小,展开精度也符合要求.这表明在控制效果上,本方法具有一定的优势.但是,本文的方法也存在一定缺点,即拉力变化较为复杂,需要做大量计算才能得到.如何在实际工程应用中使用本方法,是需要进一步考虑的问题.
[1]Cosmo M L,Lorenzini E C.Tethers in space handbook[M].3rd ed.Huntsville:NASA Marshall Space Flight Center,1997:3-10
[2]朱仁章.速率控制下的空间系绳的伸展[J].中国空间科学技术,1991,17(4):50-55
[3]黄奕勇,杨乐平.改进的绳系卫星系统距离速率控制律[J].上海航天,2007,24(3):30-33
[4]Bainum P M,Kumar V K.Optimal control of the shuttle tethered subsatellite system [J].Acta Astronautica,1980,7:1333-1348
[5]Pradeep S,Bangalore.Tension control for retrieval of tethered satellites[R].AIAA-98-4475,1998
[6]Steindl A,Troger H.Optimal control of deployment of a tethered subsatellite[J].Nonlinear Dynamics,2003,31(3):257-274
[7]Eberhart R C,Shi Y.Particle swarm optimization developments,applications and resources[C].IEEE International Conference on Evolutionary Computation,Indianapolis,USA,May 27-30,2001
The Deployment and Retrieval Control of the Tethered Satellite Based on the PSO Algorithm
WANG Wei1,LI Junfeng2,BAOYIN Hexi2
(1.Xi’an Satellite Control Center,Xi’an 710043,China;2.School of Aerospace,Tsinghua University,Beijing 10084,China)
Deployment and retrieval of a tethered satellite system is the basic issue of its application while the control scheme by varying the tension force of the tether has not been well investigated.In the article the tension force is considered as the control force and discretized in the time domain.The particle swarm optimization optimal algorithm is then used to search the optimal value fitting the optimal index in the feasible zone,thus obtaining the changing law of the control force.This control scheme can make the tethered satellite deploy to the equilibrium position in a short time under the optimal index of least swing and least time.Meanwhile,it is suitable to the retrieval.The simulation results show this control law costs shorter time and less lateral swing compared with the control law based on varying the speed of deployment and retrieval.So it has some certain advantages.
tethered satellite;deployment;retrieval;particle swarm optimization;optimal index
V412.4
A
1674-1579(2009)04-0048-04
2009-02-14
王 维(1983—),男,山西人,助理工程师,研究方向为绳系卫星动力学与控制(e-mail:wwishere@163.com).

