规则网络中多智能体系统一致性收敛速度研究

吴正平 (三峡大学电气信息学院 ，湖北 宜昌 443002)

谢学文 (大庆钻探工程公司测井二公司完井大队，吉林 松原 138003)

规则网络中多智能体系统一致性收敛速度研究

吴正平 (三峡大学电气信息学院 ，湖北 宜昌 443002)

谢学文 (大庆钻探工程公司测井二公司完井大队，吉林 松原 138003)

通过分析和仿真，对最临近耦合网络、星网络和全耦合网络的一致性收敛速度进行了研究。研究结果表明，最临近耦合网络的收敛速度是最慢的，星网络作为一个边较少的网络具有很快的一致性收敛速度，而全耦合网络是所有网络中一致性收敛速度最快的。该研究对多智能体网络的设计具有指导意义。

规则网络；多智能体系统；一致性

1 多智能体复杂网络中的一致性问题

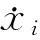
(1)

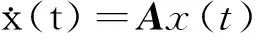
(2)

式中，x(t)={x1,x2,…,xN}为状态矢量；A={aij} ∈RN×N称为网络的耦合矩阵。记L=-A，则L为图G的拉谱拉斯矩阵。矩阵A表示网络的通信拓扑结构，如果智能体i和智能体j(i≠j)之间有通信连接，则aij=aji=1；否则，aij=aji=0(i≠j)。如果节点i的度记为ki,则有:

为了分析的方便，给出下面引理。

引理1[7]对于网络系统(2)，当A为对称不可约矩阵时，则系统(2)是收敛的。

根据引理1，笔者研究的几种规则网络对应的矩阵耦合A为对称不可约矩阵，因此相应的多智能体系统的一致性问题都是收敛的。

在开发房地产之前，必须要考虑好供求关系，这对于房价、成本计算以及开发时间和房屋的数量等起到了重要的价值，也可以促进房地产行业的发展。可以促进城市的建设，在规划当中，还需要控制风险来让规划变得更具有可行性。

引理2[8]设图L(L=-A)是强连接和平衡的，则在系统(2)中，x以速度β=λ2(L)收敛到x*。其中，λ2为L的最小非零特征值。

由引理2知，多智能体系统的拓扑结构决定了系统一致性问题的收敛速度特性，而与拓扑结构相对应的拉谱拉斯矩阵L的最小非零特征值λ2的大小度量了该系统的一致性收敛速度。

2 网络拓扑结构及其一致性问题分析

下面分析最临近耦合网络、星网络和全耦合网络的网络拓扑结构及其λ2的特性，从而进一步分析相应的多智能体系统一致性收敛速度的特性。

2.1最邻近耦合网络

在最邻近耦合网络中，N个节点围成一个环状，其中任一节点i和它相邻的节点i±1,i±2,…,i±l(l为一正整数)相连。相应的耦合矩阵Anc=(aij)N×N可以表示为:

拉普拉斯矩阵L=-Anc，其特征值为:

则当N≫m时:

(3)

从式(3)可以看出，最临近耦合网络的λ2值是较小的，因此其一致性速度很慢。

2.2星网络

在星形耦合结构中，所有的节点连接到一个节点上，该节点称为中心节点。星网络相应的耦合矩阵为:

拉普拉斯矩阵L=-Asc，其特征值为:

λ1=0λ2=λ3=…=λN-1=1λN=N

星网络的λ2=1，因此其一致性收敛速度远远大于与其具有相近平均度的最临近耦合网络。该网络的主要特点是网络连边少，网络构建成本低，一致性收敛速度快。但从其网络拓扑结构来看，当中心节点瘫痪时，整个网络也就瘫痪了，因此该网络对蓄意攻击鲁棒性差。

2.3全耦合网络

全耦合网络中每一对节点都是直接相连的网络，其相应的耦合矩阵为:

拉普拉斯矩阵L=-Agc有一单0特征值，其他的特征值均为N，因此λ2=N。在全耦合网络中，λ2的值最大，网络的一致性收敛速度最快。但全耦合网络是连边数最多的网络，因而也被认为是最复杂、构建成本最高的网络。

3 网络一致性收敛速度的仿真研究

下面，通过仿真来进一步研究最邻近耦合网络、相应的星网络(平均度约为2)和全耦合网络的一致性收敛速度。一致性问题的状态方程如式(2)所示，误差评价函数定义为[7]:

φ(x)=xTLx

初始条件均为xi(0)=i，i=0,1,…,N；节点数N=200，平均度k=2。仿真结果如图1和图2所示。

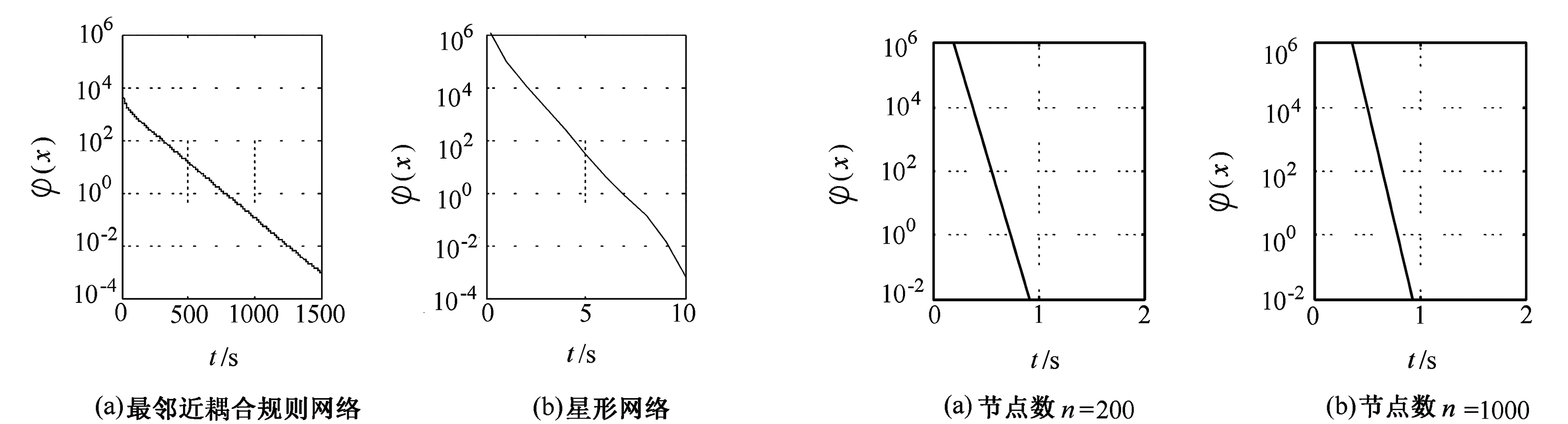
图1 误差函数 图2 全耦合网络的误差函数

从图1可以看出，对于节点数为200，平均度为2的最临近耦合网络，当误差函数值达到0.01以下时大约需要1400s，而与其节点数相同、平均度近似的星网络则只需要约8s的时间，可见，星网络的一致性收敛速度远远大于与其节点数相同、平均度近似的最临近耦合网络。

由图2可以看出，全耦合网络的收敛速度是最快的，并且和网络的规模(节点数)无关，它的一致性问题的误差函数都能在1s左右收敛到0.01以下。仿真结果与上面分析一致。

4 结 语

笔者对多智能体系统在最临近耦合网络、星网络和全耦合网络中的一致性收敛速度进行了研究。通过理论分析和数字仿真发现，星网络在通信连接较少(平均度约为2)的情况下，具有很快的收敛速度，其收敛速度要比与其具有相同节点数和相近平均度的最临近耦合网络快很多倍；全耦合网络的一致性收敛速度是最快，所有节点在1s左右即可达到一致性，且和节点数无关，但全耦合网络结构的网络通信连边数太多，当网络规模较大的时候，实现起来比较困难。

[1]Estrada E, Rodriguez-Velazquez J A. Subgraph centrality in complex networks[J].Phys Rev E， 2005，71:056103～056111.

[2]Estrada E, Rodriguez-Velazquez J A.Spectral measure of bipartivity in complex networks[J].Phys Rev E, 2005，72: 046105～046110.

[3]Zhengping Wu, ZhiHong Guan, Xianyong Wu，etal.Consensus Based Formation Control and Trajectory Tracing of Multi-Agent Robot Systems, Journal of Intelligent and Robotic Systems[J].Springer Netherlands, 2007, 48:397～410.

[4]Zhengping Wu, ZhihongGuan , Xianyong Wu.Consensus problem in Multi-Agent Systems with physical position neighborhood evolving network[J].Physica A,2007, 379:681～690.

[5]Saber R O. Ultrafast consensus in small-world network[A].Proc. ACC, Portland, OR, 2005, 4:2371～2378.

[6]Saber R O, Murray R M. Consensus problems in networks of agents with switching topology and time-delays[J].IEEE Trans Automat Contr, 2004, 49(9):1520～1533.

[7]Ren W , Beard R W. Consensus of information under dynamically changing interaction topologies[A].Proc 2004 ACC, Boston, MA,2004.4939～4944.

[8]Saber R O, Murray R M. Agreement problems in networks with directed graphs and switching topology[A].In Proc 2003 CDC, 2003,4:4126～4132.

[编辑] 易国华

TP273

A

1673-1409(2009)02-N060-03

2009-02-24

吴正平(1966-)，男，1988年大学毕业，博士，副教授，现主要从事复杂动态网络和复杂非线性系统以及检测技术与自动化装置等方面的教学与研究工作。