基于熵组合预测模型的害虫种群动态研究

梁 铃 (长江大学园艺园林学院，湖北 荆州 434025)

贾伟宽，王 慧 (山东农业大学植物保护学院，山东 泰安 271018)

基于熵组合预测模型的害虫种群动态研究

梁 铃 (长江大学园艺园林学院，湖北 荆州 434025)

贾伟宽，王 慧 (山东农业大学植物保护学院，山东 泰安 271018)

在农业害虫种群动态的研究中，单一预测模型很难达到理想的预测精度。组合预测模型是将不同的预测模型进行适当的优化组合，以综合利用各单项模型的预测信息，以提高预测精度，然而组合预测模型的核心问题是所综合的模型权重的确定。运用信息熵理论，根据测度不确定性的函数确定组合模型的权值，建立了基于信息熵的组合预测模型，以期在研究昆虫生态中应用。将新建立的预测模型在玉米蚜种群动态研究中进行仿真实验，验证了新模型的有效性。

组合模型; 预测预报; 熵权; 种群动态

目前，农作物的虫害已严重制约着农作物的丰产丰收，使农业经济遭受巨大损失。若对害虫的发生能早期作出预报，及时采取防治措施，可使虫害对农作物危害造成的损失减少到最低。农业害虫种群动态受环境的影响十分明显，各种影响因素相互干扰，具有很强的不确定性，所以预测起来十分困难。测报的精确性和有效性一直是制约农业害虫有效防治的瓶颈，在测报的方法选择和模型的建立还有待于进一步的研究[1]。在当前的害虫测报模型中，往往采用一个固定的模型，不同模型原理和出发点不同，预测过程中考虑的影响因子侧重点亦不同，不同的预测模型往往只能提供某一方面的有用信息，不可避免地会丢失另外一些有用信息,致使单一的模型难以达到理想的测报结果。

组合预测[2,3]是近年发展起来的一种有效的综合预测方法，在其他领域已经得到很好的应用[4～9]，但该模型在农业害虫种群动态的预测中的应用还很少有报道。组合预测原理是将不同的预测方法进行适当的组合，以综合利用各种方法所提供的信息，尽可能提高预测精度。组合预测的核心问题是权重的确定，本研究采用基于信息熵理论确定组合模型的权系数。该方法的特点是直接全面研究各个体预测方法的误差指标值以最终确定各个体预测方法在组合预测模型中的权重，从而使新的组合预测模型能充分利用各个体预测方法所包含的显信息和隐信息, 使预测结果更科学、更客观。本研究还通过对玉米蚜种群动态的研究测试，证明了模型的的可靠性。将组合模型应用于害虫种群生态研究，可为害虫的预测预报提供新的方法，提高测报的可信性。

1 基于信息熵的组合预测模型

1．1 信息熵原理

信息熵是Shannon信息论中的重要概念[10]，是把熵作为一个随机事件的“不确定性”或信息量的量度。信息量是信息论的中心概念，是信息论度量信息的基本出发点，是把获得的信息看作用以消除不确定性的因素。因此信息量的多少，可以用被消除的不确定性的大小来表示，而随机事件不确定性的大小可以用其概率分布来描述。

通过概率空间来描述信息量，设设有一离散型随机变量X，其n个可能的取值为x1,x2,…,xn，每一取值出现的概率分别为p1,p2,…,pn。则X的概率空间可表示为[X,P]，用pi表示事件{X=xi}发生的概率，且0≤pi≤1。[X,P]完整地描述了由X所代表的离散信源的特性，也被称为X的信源空间。设称为信息函数，表示{X=xi}事件发生之前表示其不确定性；若{X=xi}事件发生后则表示xi的自信息量。

I(xi)=-logpi(i=1,2,…,n)

1．2 基于熵的组合模型

组合模型的核心问题是如何确定所组合的各单一模型的权重，目前较多采用的是人为定义、负变、最小二乘等方法确定权重。这些方法，虽在一定程度上解决了权值求解问题，然而却没能很好地顾及权值所隐含的信息度量问题。

于是得到m个模型的加权组合预测模型

利用信息论中熵的定义来求解模型中的W，根据熵的定义可以得出

预测误差衡量的是预测值偏离实际值的程度，因此在这里取绝对值

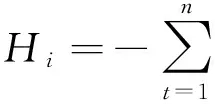
对应的熵权应该为

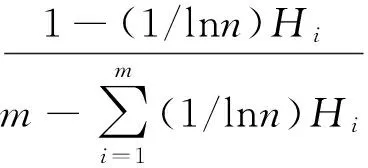
但是在求权重的时候注意这个问题，也就是求权重的原则是误差的熵的绝对值越大对应的权重应该越小，所以求出熵权后对其进行一定的变换，求倒数。所以所求权重为

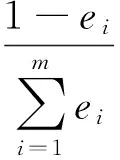
利用求出的权重带入组合模型，得到组合预测误差值以及误差平方和。求出组合预测误差求出组合预测值。误差越小权重越大。

2 实例应用分析

本研究以分析山东宁阳县1989～2000年的玉米蚜种群发生情况为例(所用数据由山东宁阳县植保站提供)。玉米蚜的发生受多种因素制约，如气象因素(温度、降水、相对湿度、日照时数等)、虫源基数、当年小麦的种植面积、耕作制度以及灌水条件等等。由于当年小麦种植面积数据不完整，耕作制度和灌水条件也无法作定量的分析，这些方面的因素无法用于预测预报。这里选择用7～9月份的月平均气温、月平均降水量、月平均相对湿度，卵的数量作为预测因子。

先采用多元线性回归模型F1，该模型简单易懂、便于操作计算，目前在国内害虫测报中占统治地位，然而害虫的发生与预测因子间并不是单纯的线性关系。多元多项式回归模型F2可以看作是多元线性回归的改进，然而却主要顾及统计方面的知识，一定程度上忽略了生物学因素。BP模型F3是处理非线性问题较好的工具，然而该模型更适合处理复杂的大规模的非线性动态时变系统问题。应用这3种模型对玉米蚜种群发生序列进行预测，将得到的预测值以及计算得到的误差平方和(Error Sum Squares, SSE)列于表1。

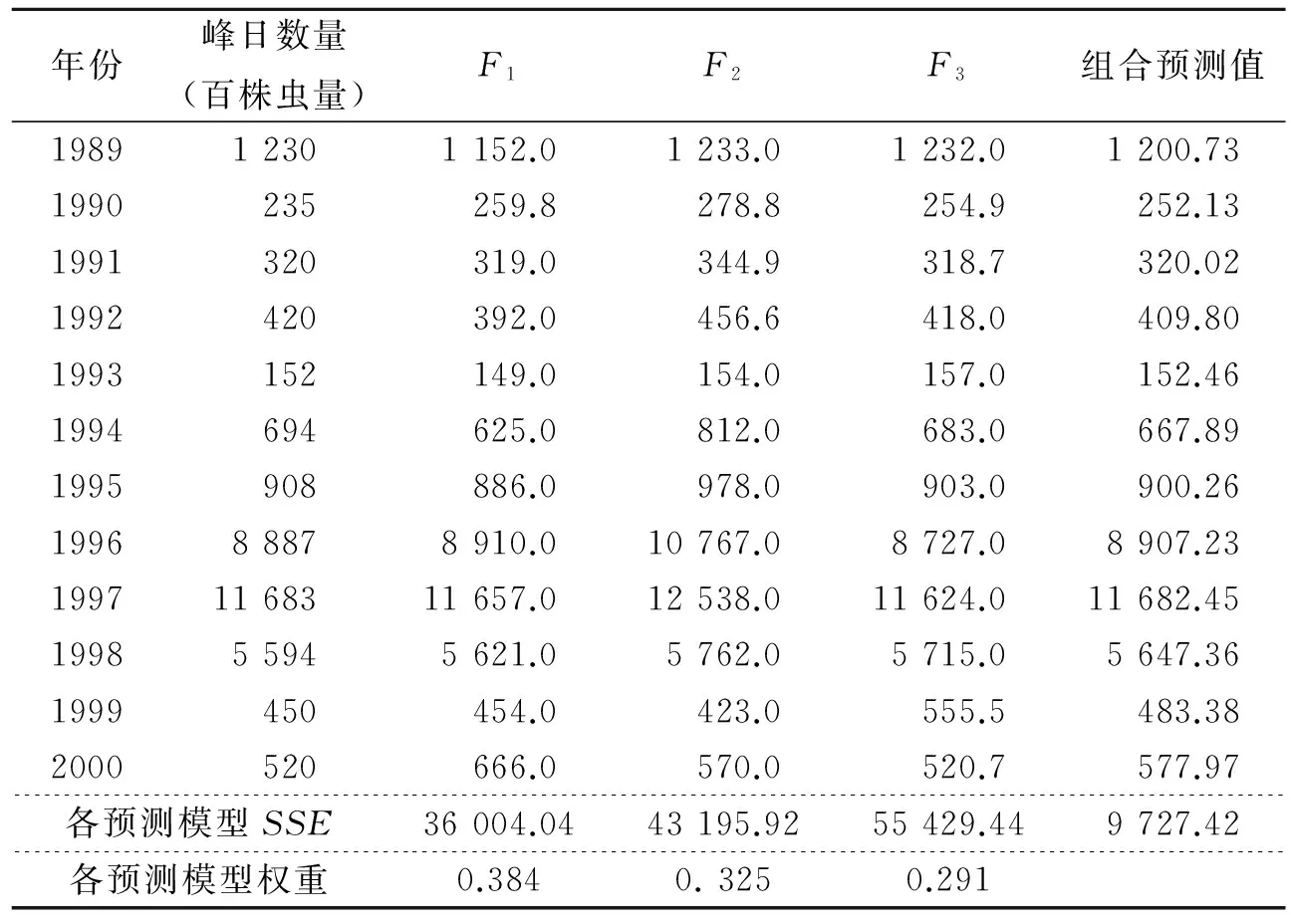
表1 各模型预测值、误差平方和以及单项模型权重Table 1 Forecasting value,SSE of each model and weight of single model

再采用前面所建立的组合模型，对该问题进行模拟分析，运用1.2中的算法步骤确定各单一模型的权值，可得组合模型F=0.384F1+0.325F2+ 0.291F3，同样将处理结果列于表1。

由表1可以看出，组合模型的预测结果明显优于用单一模型的预测结果;再从计算的误差平方和看，组合模型要明显小于其他单项模型。可以判定组合预测模型在农业害虫种群动态的预测中是切实可行的。组合预测模型应用于害虫预测预测，以期为研究害虫生态提供一种新的方法。

3 结论

组合预测是研究复杂系统非线性变化的十分有效的方法，通过对单项模型的适当组合，充分利用了原始数据中的信息，避免了单一理论方法的局限性，提高了模型的精度，使得预测误差有很大程度的减小，对历史数据的拟合度有很大程度的提高。在对组合预测模型进行优化时，不同方法得到的结果不同，寻找适合具体研究对象的优化方法是组合模型研究的重点。

在应用组合预测模型时，要充分研究预测对象的特点和变化规律，采用能够反映预测对象变化特点的单项预测方法。从上述结果可以看出，组合预测模型比其他单项预测模型有更高的预测精度，达到了运用组合预测寻求更好预测结果的目的。同时说明运用熵权法寻求组合预测模型的权重系数是有效的。目前的农业害虫预测预报仍然停留在寻求精确的数学模型以便最大限度提高预测精度的阶段。组合预测由于其综合利用各单项模型的预测信息，能够进一步提高预测精度，受到许多预测专家的青睐。

在统计预测预报中，寻求最好的模型拟合效果仍然是农业害虫预测预报中的主要思想。然而农业害虫的发生发展有着深刻的环境制约，而环境的变化是很难把握的，很难运用精确的数字或者模型进行描述，因此在追求预测精度逐步提高的同时也要考虑农业害虫发生发展的模糊性和复杂性。农业害虫种群动态受到各种因素的制约，各种因素往往互相影响，很难用精确的数学语言进行描述，具有很强的模糊性，在运用组合预测模型时要充分考虑害虫种群动态的这种特点，综合利用预测对象提供的各种信息，最大限度的提高预测的精度。针对农业害虫种群的特点 ，在应用组合预测模型进行预测时，如果能够将模糊数学[11]、灰色理论[12]等现代数学方法结合起来，该方法将会有广阔的应用前景，这有待进一步的研究。

[1]马 飞, 程遐年. 害虫预测预报研究进展(综述)[J].安徽农业大学学报,2001, 28 (1): 92～97.

[2]唐小我.预测理论及其应用[M].成都:电子科技大学出版社,1992.

[3]Bates J M, Granger C W J. Combination of forecasts[J]. Poerations Research Quarterly, 1969,20(4): 451～468.

[4]张 星, 吴菊薪, 陈 惠，等. 基于熵权的福建粮食产量组合预测模型[J]. 中国农业气象, 2008, 29 (2) : 194～196.

[5]谢正文, 胡汉华. 基于熵权的灰色沉降组合预测模型及应用[J]. 矿业研究与开发, 2007, 27(4): 12～13.

[6]陈华友. 熵值法及其在确定组合预测权系数中的应用[J]. 安徽大学学报(自然科学版), 2003, 27(4): 1～6.

[7]刘兵军. 电力负荷组合预测权重的确定[J]. 电力情报, 2002，(2): 16～17.

[8]马永开, 唐小我. 线性组合预测模型优化问题研究[J]. 系统工程理论与实践. 1998，(9): 110～114.

[9]熊崇俊, 宁宣熙, 潘颖莉. 基于熵的组合预测法研究[J]. 科技进步与对策, 2006，(4): 68～69.

[10]Shannon C E. A mathematical theory of communication[J]. The Bell System Technical Journal, 1948, 379～423.

[11]陈国华, 陈 收, 汪寿阳. 区间数模糊投资组合模型[J]. 系统工程, 2007, 25(8): 34～37.

[12]谢孝如, 蒋惠园, 申耀伟. 基于并联灰色-线性回归组合模型的客运量预测[J]. 铁道运输与经济, 2008, 30(8): 92～94.

2008-12-29

梁 铃(1981-)，女(仫佬族)，广西河池人，理学硕士，助教，主要从事分子生物学研究.

10.3969/j.issn.1673-1409(S).2009.01.002

S431.9

A

1673-1409(2009)01-S005-03