初中数学教学还欠缺什么

郭　梅

一、缺少兴趣的激发

根据美国心理学家伯克曼的分析:兴趣和需求是人们行为的两大动力。没有动力,人是不会主动地做一件事的。学生由于年龄小,往往看不到学习知识的必要性,感觉不到自己有这方面的需求。因此,我们必须利用学生的好奇心,引起学生的兴趣,激发学生的思维。一个人最感兴趣的事,也一定是他最有可能干好的事。

例1:在教“三角形内角和”时,由于对“三角形三个内角的和等于180°”这一结论学生早已知道,我们先问他们是怎么得出来的?有的学生用折纸的方法,有的干脆将三个角剪下拼在一起,我在肯定了同学们的积极思维的同时又提出疑问:画在黑板上的三角形能用这样的方法吗?你有什么新方法?疑问使同学们产生好奇,好奇心又转化为强烈的求知欲望,同学们跃跃欲试。在动手操作中,在小组讨论中,终于发现了三角形内角和定理的多种证法。

二、缺少知识的探索过程

学生的学习只有通过自身的操作活动和再现创造性的“做”,才可能是有效的。也可以说,数学是做出来的,不是教出来的。一个学生,没有活动,没有“做”就不会形成学习。数学教学过程必须重视让学生亲身感受、动手操作、动口交流。

学生的学习只有通过自身的情感体验,才有可能树立起学会、学好的自信心。而只有使学生具有了这种自信心,才能算是成功的教学,教师要为学生提供一个体验成功与挫折的舞台。

例2:在教“角平分线”时,我这样设计:

1.有一张剪好的角的纸片,怎样找到这个角的平分线?

(对折,如图1)

2.如果把对折的纸片继续折一次,然后把纸片展开,观察折痕,你能发现什么结论?说明你的理由。(PM=PN,如图2)

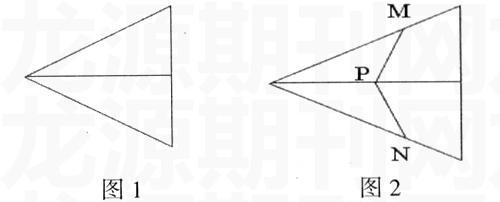
3.上述等长折痕PM和PN,你能找到多少对?有特殊位置的线段吗?

学生认真操作、观察、思考、实践,终于发现了“角平分线上的点到角的两边距离相等”这一结论。

三、缺少数学思想与方法形成过程的引导

初中数学内容尽管很简单,但其中蕴含着最基本的数学思想与方法。很多老师虽然注意到要使学生会用这些思想和方法处理实际问题,但所用的方法不妥当。

如:辅助线是几何证题的桥梁,恰当地引出辅助线是证题的关键,但不少老师往往是先作辅助线,再讲这种方法的妙处,没有说明为什么要这样做的原因及其形成过程,一种方法必有其形成的背景,对此教师应加以剖析、引导。

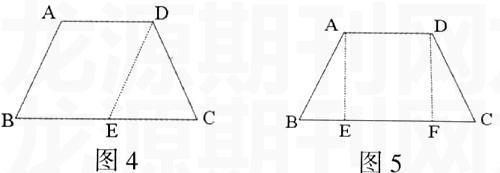
例3:在证明“等腰梯形同一底上的两个角相等”时,可作如下引导:

要证∠B=∠C,即证两角相等,有哪些方法?

1.利用等腰三角形,没有等腰三角形,怎么办?

导出图4辅助线的作法。

2.利用全等三角形,如何找全等三角形?

导出图5辅助线的作法。

教学时应使学生明确,每种辅助线作法的产生是根据解题的需要,是受到一些“好念头”的启发。教师教给学生的不应只是精妙绝伦的解题方法,更应是发现这种方法的思路和途径。

四、缺少对学生思维调整及整合过程的指导

学生的认知过程是一个对思想不断进行自我调整、整合的过程,教师对此应加强指导。如今课堂教学中思维“失真”现象较为严重,一方面,教师呈现给学生的是优化的思维方式和完美的解题过程,难以体现出教师思维的真实过程,使得学生只会模仿,不会创新;另一方面,学生回答问题时,只能沿着教师的思路回答,若有一点出格的想法,往往会被教师扼杀在萌芽状态,掩盖了学生思维活动的真实过程。这种现象屡屡出现,其表现是当学生与教师的思路不一致时,教师往往是不予板书或示意学生中断回答,即使学生思路正确也不能引起教师足够的重视。其根源是教师担心学生的“打岔”会影响教学进程,导致不能完成当堂课的任务,教学效率不高。

其实,教师应该认识到数学课堂教学的效率不能与“生产效率”相等同,课堂教学中学生思考问题的深广度、认知结构建立的合理和稳定的程度等都是无法用“率”来度量的,而这些恰恰是数学教学的核心。

对“迷路”的学生,不要马上给方向,而应给“指南针”,让学生自己试着定向,对“走错”的学生,也不要马上否定,要尽可能多地肯定学生思维的合理成份。要留时间让学生思考,让学生去尝试错误,在试误过程中积极思考和探索。

五、缺少“开放题”的设计

数学题型的改革是实行数学素质教育的突破口,数学教学的范例和练习题应由目前的“封闭式”习题转变为“封闭性”与“开放性”相结合的习题。

2000年戴再平以三个开放题和几个封闭题在浙江省镇海县三所程度不同的学校各取一个初三班级进行了一次测试,结果如下:

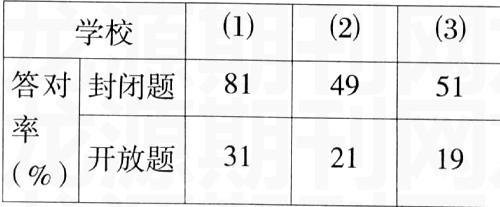
测试所用的开放题之一是:

试指出下列两个代数式的共同点:

12a2b2c;8a3xy

测试说明了知识和技能的堆砌与学生创造思维能力的发展没有必然的联系。2003年,胡林瑞对安徽省黄山市屯溪二中51名初三和高三学生,用5道外国开放性数学题作一次测试,得出“高中生解这类题的能力并不比初中生强,他们虽然多读了3年书,知识和技能上可能多一些,但发散性、创造性思维能力都无甚增长”的令人惊讶的结论。

他进一步分析:“这也许能说明在进行基础知识教学的同时,如果不引导学生去进行‘发现,不注意培养学生思维品质,而只要求学生‘记公式定理,套题型解法,则有可能导致学生思维发展的停滞,聪明才智的被扼杀。”这些调查都说明,数学开放题对培养学生创造能力的必要性。

例4:为了复习三角形全等的几种判定方法,我曾设计了这样一组题:

1.图6中△ABD与△ACD,需要哪些条件,并且只需要这些条件,这两个三角形就全等。

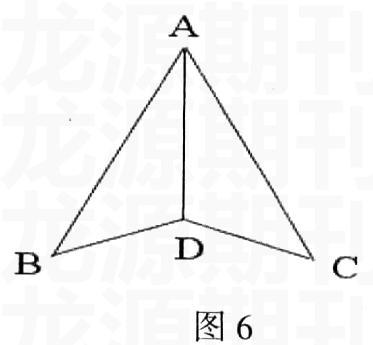
2.请根据上面给出的条件,编写证明题。

3.如图7,已知:AB=AC,BD=CD,E是AD延长线上一点,

求证:BE=CE

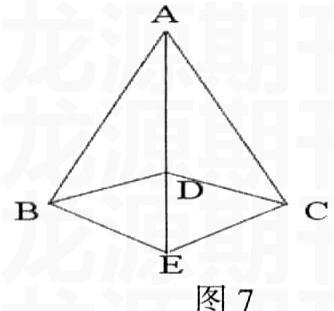
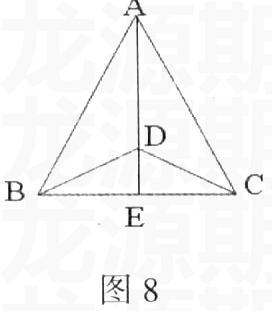
4.如图8,已知:AB=AC,E是BC中点,根据所给出的条件,你能得到哪些结论?并说明理由。

六、缺少学生知识缺陷“病历”的建立

我们常会遇到这种情况,当问学生哪些知识完全不懂时,很少有学生能准确地说出自己哪些知识完全不懂,哪些知识只掌握到哪个层次。只感觉到:一听就懂,一做就错。而老师对此也不甚了然,无法有针对性地把学生的知识缺陷补上。由此可见,教师为学生建立知识缺陷“病历”就显得至关重要了。

“病历”建立的途径就像医生给病人诊病一样,可结合多种形式和手段,如通过作业检查、测试、课堂提问、谈话,等等,具体到每一个知识点、每一种题型,每一位学生的能力记录到“病历”上。当然教师对此不仅要坚持不懈,用长期的时间和精力进行总结、归纳、分析等,而且还要随时根据学生的变化进行修改。

教学的过程实际上是个相互影响的过程。你想真正影响他,就必须先了解他,根据他的情况不断调整自己的教育思想、思路和方案以及方法,这个过程要花费很大的精力,但却能取得较好的效果。

(责任编辑:贾腊生)