小学数学中几个重要量的教学

岳德明

一、量、计量单位及计量的基本含义

量，是数学中的一个基本概念。例如，我们要经常测定生活、生产中的某些事物存在规模和发展程度的多少、大小、长短、厚薄、速度等属性，那么这些可以测定的对象就是量。量有连续量与不连续量之分。小学中，一般不给“量”下严格的数学定义。

为了真实地测定出某个量存在的规模和发展程度，就需要一个约定的“标准”。那么，用来作为测定量的这个标准就叫做计量单位。每一种测量工具都有计量单位，而且测量同一类量的计量工具还有不同程度的计量单位。例如，长度计量单位有厘米、分米、米等，面积单位有平方厘米、平方分米、平方米等。因此，用一种测量工具测定同一个量，得到的量数也不一样。用1cm计量单位的工具去测量一条线段，最得的结果是3cm，也就是说，这条线段的长度是这个计量单位的3倍，那么，这个3就叫做1cm的量数；如果用计量单位1m的工具去测量该线段的长度时，量得的结果是0.03m。同一个量随着测量工具的计量单位变化，所得到的量数也不一样。

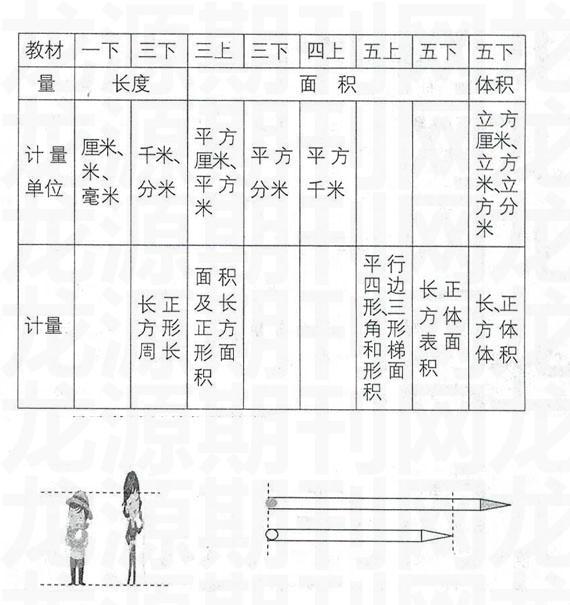
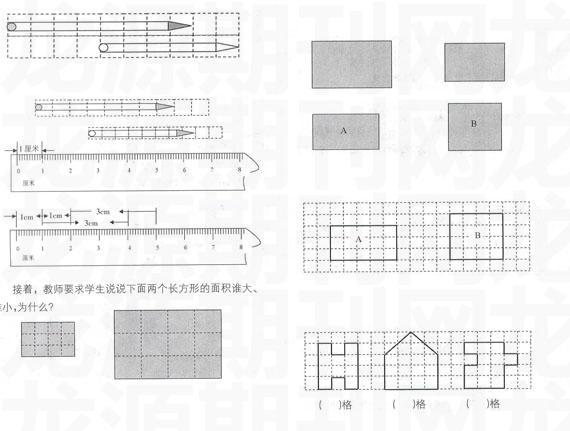
由此可见，所谓计量，是指把一个约定的标准量与一个未知量作比较的过程。如要测量一条线段的长度，就要用一把有刻度的尺去量这条线段，有刻度的尺是标准量，需要测量的线段长度是未知量，用尺测量线段长度的过程就是计量。

传统上，说起计量往往会被理解为度、量、衡：度是用计量工具尺计量长度，量是用计量工具升计量容量(液体)，衡是用秤计量工具计量重(质)量。事实上，度、量、衡只是计量中的一小部分。可见，计量实际上是运用计量工具测定被计量对象属性多少、大小、长短、厚薄、快慢等的活动。

用计量工具计量某个量后，就得到这个量的量数。这个量数有大有小，就可以用数来反映。量数(数)与量的计量单位联系起来就能清楚、准确地反映量的属性、程度。那么，将一个量的量数并附上计量单位的总称，就是数量。像3cm、0.03m等就是数量。数量能清楚、准确地反映量的属性、程度。

二、几个重要量的教学

小学数学教材(上教社，下同)中，学生所要学习的量很多，其中长度、面积、体积等几个重要的量更需要扎扎实实学习好。学生学习某个量，将依次需要学习量的概念及其计量单位和计量方法等知识。

1量其计量单位的教学

量有大、有小。大与小是相对而言的，只有通过对量进行比较后，才能说一个量比另一个量大，或一个量比另一个量小。学生在生活中也已经积累了不少有关量的生活经验。因此，教学时除了采用比较的方法外，还应发挥学生的生活经验，并引导他们从“半生活半数学的量”，逐步走向数学意义上的“量”。

案例长度及其单位的教学

长度是指平面上两点间的距离。在小学数学中一般不给长度下定义，而是从学生的生活经验出发，用比较入手，逐步引导他们感受、建立长度经验。首先，让两名同学比身高(长)，两支铅笔比长短。学生有经验，只要将

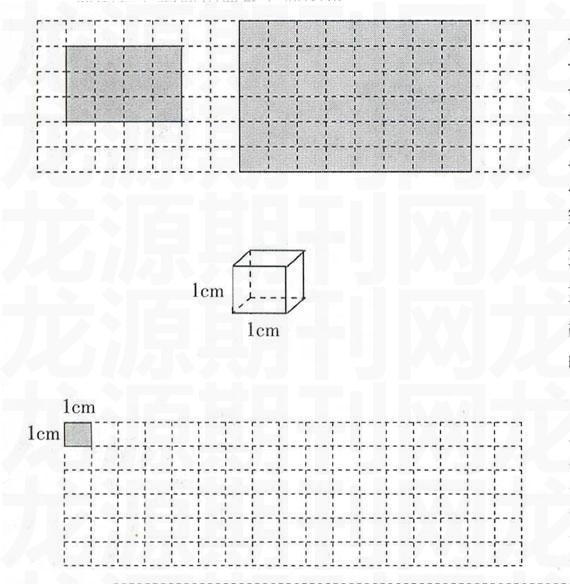
两者的一端对齐，看另一端，另一端长就长、另一端短就短。初步建立长度观念。

但是，一支铅笔到底有多长，一支铅笔比另一支铅笔到底长多少，这就需要借助“第三者”来进行定量比较才公平。把两支铅笔放在每小格完全相同的方格纸上(如下图所示)，就可看出上面一支铅笔占8格，下面一支铅笔占6格，上面一支铅笔比下面一支铅笔长2格。学生在用方格纸比较长度中知道要比较两个量分别是多少，或一个量比另一个量长多少，可借助“第三者”来比较，而且还可用自己的脚步、眼等“计量单位”进行比较，以进一步积累长度经验。

接着，教师让学生经历需要建立一个统一长度计量单位的活动。教师让学生将两支铅笔再放在两张方格纸上(如下图)，并比较两支铅笔哪支长。这时，学生在认识上发生冲突，上面一支铅笔长占8格，下面一支铅笔长也占8格，“一样长”。明明是上面一支铅笔比下一支铅笔长，现在怎么会一样长呢?他们强烈地感受到需要用一个统一的格子(计量单位)去比较两支铅笔，才能真实地比较出两支铅笔的长短，产生学习统一的长度计量单位的心理需求。

在此基础上，教师介绍计量工具尺，并教学长度计量单位“标准量”厘米。教师让学生拿出直尺，找到0刻度线、1刻度线、2刻度线……在数学上，从0刻度线到1刻度线的长度是1厘米(如下图)。1厘米“就是测量铅笔长度的统一格子”，与学生的手指宽度差不多。教师要求学生再举例，生活中哪些物体的长度大约也是1厘米长，帮助他们建立1厘米的长度表象。

学生认识长度计量工具及单位后，教师让他们在尺上指出1厘米、2厘米、3厘米等“线段”，感受直尺上就有许多线段：从0刻度线到2刻度线间有2个1厘米，是2厘米；从1刻度线到4刻度线间有3个1厘米，是3厘米……

最后，教师要求学生用直尺测量铅笔长度、小刀片长度……使他们体验物体有长度，并可用统一长度单位的尺准确地测量出来，不断积累长度经验。长度经验及其计量单位表象的建立，又为学生学习其他长度单位打下扎实的基础。

案例面积及其单位的教学

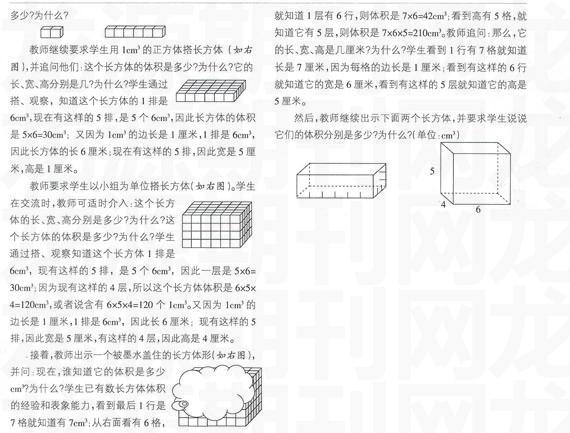
教师先让学生拿出两个太小显著的长方形(如下图)，要求他们用水彩笔“匀速”地涂两个长方形再比较大小；也可让学生用视觉直接比较大小，还可用重叠的办法比较。教师再跟进：左面长方形比右面长方形大，在数学上就说左面长方形的面积比右面长方形的面积大，或者右面长方形的面积比左面长方形的面积小。通过定性比较，帮助学生初步感知面积经验。

那么，两个平面图形比较面积大小，其中一个图形的面积比另一个图形面积到底大多少?教师再从长方体和正方体教具上分别撕下两个平面图形(如下图)，并要求学生说说哪个图形的面积大一些，大多少?

这时，教师要求学生把透明方格纸盖在A、B两个图形上并问：现在知道这两个图形的面积谁大、谁小了吗?谁比谁多(少)多少了吗?学生通过数方格，知道A图形有15小格，B图形有16小格，所以A图形比B图形小，A图形比B图形小l格。教师跟进：在数学上，我们就说A图形的面积比B图形的面积小，或者说，B图形的面积比A图形的面积大。逐步从定性比较走向定量比较。

教师再要求学生用数方格的方法，说出下面平面图形的面积，并揭示面积的基本含义：(所谓)平面图形或物体表面的面积，指的就是它们的大小(情况)。

接着，教师要求学生说说下面两个长方形的面积谁大、谁小，为什么?

此时，学生认知上又发生了矛盾，体验到仅凭数格子无法真实地反映两个长方形面积的大小，同时也催生出需要学习统一面积计量单位的强烈心理需求。教师随即让学生将方格纸放在两个长方形上面，再数格子，比较两个长方形的面积。学生立刻发现一个12小格，一个48小格，显然左面的长方形面积要比右面的小。

此时，学生学习面积计量单位水到渠成。教师要求学生用尺量出方格纸1格的边长长度，并跟进：边长1厘米的正方形，面积是1平方厘米：再帮助他们建立1平方厘米的表

象：那么，生活中哪些图形或者物体表面的面积与1平方厘米差不多?学生举出1格作文纸、1小块修正纸、手指甲的表面等。

最后，教师让学生在方格纸上涂出1平方厘米、2平方厘米、5平方厘米等图形，使他们感受到这张方格纸可以计量平面图形的面积。

案例体积及其单位的教学

在长度、面积、体积三个重要量中，体积概念更难理解。但是，学生在生活中还是积累了许多体积经验，像大人与小孩、讲台与课桌等，因此，体积概念的教学也应借助学生的生活经验，并采用比较的方法。

实际上，学生理解“空间”比理解体积似乎更困难。教师呈示一只里面已经装了一些货物的集装箱：集装箱里面还能装货物吗?为什么?学生感受到集装箱里面还能装货物，因为里面还有“空间”。教师说：对!并呈示课件，继续往集装箱里装货物，直至装满。这说明物体占有空间。接着，教师让学生举例，学生举出铅笔盒占了书包的一些空间、书包占了课桌抽屉的一些空间……教师跟进：那么，谁占的空间大?谁占的空间小?显然，书包所占的空间要比铅笔盒所占的空间大，或者铅笔盒所占的空间要比书包所占的空间小。

在此基础上，教师可以进行三个层次的教学，帮助学生不断丰富、积累体积经验。第一，将两个“相似”物体，大小明显到可用视觉加以确认后，想象一个物体包含在另一个物体之内。例如，大象身体与老鼠身体比较，谁占的空间大?学生通过视觉就能知道大象身体能包含老鼠身体(学生语“老鼠钻入大象的鼻子内”)，显然，大象身体所占的空间比老鼠所占空间大。那么，数学上，把物体占的空间的大小叫做物体的体积。在这里，就说成大象身体体积比老鼠身体体积大，使学生初步形成物体体积具象。再如，集装箱体积与里面所装货物的体积和比较，谁的体积大?显然，集装箱的长、宽、高都大于里面货物的长、宽、高，也就是说大长方体包含了小长方体，因此，集装箱体积要比里面所装货物的体积和大。

第二，教师让学生用两个特殊的物体——长方体，对其进行长、宽、高的两两直接比较，例如，让学生拿出两本书，分别比较它们的长、宽、高，并让大家边比较、边观察、边说说谁的体积大，谁的体积小：如果两本书的封面面积(长、宽一样)一样大，那么比厚，哪本书厚那本书的体积就较大；如果两本书的宽、厚一样，那么比长，哪本书长那本书的体积就较大：如果两本书的长、厚一样，那么比宽，哪本书宽那本书的体积就较大。学生感受到长方体所占空间的大小受它的长、宽、高影响，比较两个长方体的体积大小要看它们的长、宽、高，以区分“空间大小”与“面积大小”，发展空间观念，进一步积累体积经验。

第三，如果难以直接比较两个物体体积的大小，就需要进行间接比较。学生会把甲乙两杯水(体积)倒入同一个长方体玻璃缸内，并发现甲杯水高一些，乙杯水低一些，进而判断出甲杯水体积比乙杯水体积大。

紧接着，教师让学生观察、思考，把甲杯水倒入长方体玻璃缸内后，水的体积前后是否发生变化?使他们知道在不计算损耗的情况下体积具有守恒性。学生知道了物体体积的守恒性，对他们计算组合体体积有着重要的帮助。

学生通过学习长度、面积概念及其计量单位后，已有经验，要计量一个物体的体积，同样需要统一的体积计量单位。因此，教学体积计量单位时，可以开门见山。教师首先出示一个长方体和一个正方体，让学生直接比较它们的体积，并问：那么，这个长方体体积到底是多少呢?这个长方体体积比这个正方体体积到底大多少呢?这与计量长度、面积一样，要计量一个长方体的体积，同样需要有统一的体积计量单位。

接着，教师要求学生拿出一个正方体学具，量一量它的棱长是多少厘米，并说像这样棱长是1厘米的正方体，它的体积是1立方厘米(如右图)，这就是计量物体体积的一个计量单位。

然后，教师再要求学生用橡皮泥捏一个大约是1cm³的正方体，或用小刀片在橡皮泥上切下一个约1cm³的正方体。再让学生想想、说说生活中，哪些物体的体积也与1cm³的体积差不多?大家会举出骰子、铅笔的橡皮头、开关按钮、粉笔头等物体，以帮助他们建立1cm³的表象。

最后，教师要求学生用几个1cm³的正方体搭积木，并说出它们的体积是多少立方厘米，为什么。

2量的计量的教学

量的计量方法有两种，一种是直接计量，如以上用尺计量线段的长度，用1平方厘米的方格纸计量平面图形的面积等，都是直接计量。另一种是间接计量。所谓间接计量，是指有时需要先计量有关的量的程度，然后通过计算才能得到所需的计量结果，例如先用尺量出正方形的边长，最后再计算出正方形的面积，就是间接计量。因此，我们也可以将计算长(正)方形面积、长(正)方体体积的方法看作是一种间接计量。在用计量单位直接计量的时候，一定要注意引导学生从直接计量走向间接计量(计算)。

案例用量角器计量角的教学

这里，举一个用量角器直接计量角的度数的例子。

教学时，可把量角器的认识与计量角结合起来。教师直接让学生在量角器上找角，学生可能先找到平角、直角等特殊角。教师追问这些角的顶点在哪里(在量角器上又叫“中心点”)，并用课件呈示；角的两条边在哪里(在量角器上又称“刻度线”，其中左右两条刻度线都叫零刻度线)，并用课件呈示，使学生对量角器结构有个比较好的认识，又知道量角器上有各种角，为探索“线边重合，点点重合”做好了铺垫。

接着，教师要求学生在纸制量角器上先画出角，再说出角的度数，并追问：你是从哪里数起的?是数外圈的还是数内圈的?或者是从左零刻度线开始数起的?还是从右零刻度线开始数起的?引导学生知道用量角器上的角去计量被量角的度数时有两个起点，既可以从右(外)零刻度线开始数，又可以从左(内)零刻度线开始数，为他们“读出度数”提供铺垫。

然后，教师就要求学生用量角器去尝试计量被量角的度数。学生在交流中，教师不断追问，当学生先把量角器的一条零刻度线与角的一条边重合时，追问：第二步做什么?学生答：把量角器的中心点与角的顶点重合，再问：你是怎样使量角器的中心点与角的顶点重合的?学生答：移(平移)过来，最后再读出度数；当学生先用量角器的中心点与角的顶点重合时，教师又追问：接着做什么?学生答：旋转量角器，使一条零刻度线与角的一条边重合，最后读出度数，以帮助学生获得量角的“动作技能”。

学生通过独立量角，小组交流量角方法，全班反馈量角步骤，并在教师及时、适度的引导下，建构起量角技能：先线边重合，再平移使点点重合；或先点点重合，再旋转使线边重合；最后读出度数。即线边重合，点点重合，读出度数。

案例计算长(正)方形面积的教学

首先，教师让学生拿出一个长方形和正方形，并问：它们的面积分别是多少?你有什么办法?

学生根据经验用计量工具方格纸盖在长、正方形上面(如下图)，得到长方形面积是15平方时厘米，正方形面积是16平方厘米。

这时，教师要十分注意引导学生从用直接计量长、正方形面积逐步抽象到用间接计量——计算长、正方形面积的方法(公式)。教师追问：你是怎样数出来的?有学生是1cm²、1cm²数的。但也有学生会用巧妙的办法数，一行有5个1cm²，是5cm²，有3行，因此是3个5cm²，即3×5=15cm²；还有学生先数一列有3个1cm²，是3cm²，有5列，所以是5个3cm²，是5×3=15cm²。教师应对学生的巧数方法予以充分的肯定。

接着，教师出示一个被墨水盖住了的长方形(如下左图)，并问大家：现在，谁还能知道它的面积是多少cm²?为什么?学生这时已有巧数长方形面积的经验，他们看到最后1列有4格是4²，有这样的6列，因此这个长方形的面积是6×4=24cm²。教师继续出示右下图：现在，谁还能知道这个长方形的面积?为什么?学生看到这个长方形的宽有5格，就知道它一列有5个1cm²，长有7格，就知道它有这样的7列，所以，这个长方形的面积是7×5=35cm²。

教师再出示一个长11厘米，宽6厘米的长方形(下图)，并问学生：现在，谁还能知道它的面积是多少?为什么?此时，学生已经有了一定的表象能力，看到宽6厘米，就想象这个长方形的一列有6个1cm²，是6cm²；长11厘米，就想象这个长方形有这样的11列，所以得到这个长方形的面积是11个6cm²，即11×6=66cm²。

最后，教师要求学生议一议，并归纳出直接计量长方形面积的方法：长方形面积=长×宽(或宽×长)。

案例计算长(正)方体体积的教学

教师先要求学生用1cm³的正方体搭长方体(如下图)，并追问它们的体积分别是多少?为什么?它们的长、宽、高分别是多少?为什么?

教师继续要求学生用1cm³的正方体搭长方体(如右图)，并追问他们：这个长方体的体积是多少?为什么?它的长、宽、高分别是几?为什么?学生通过搭、观察，知道这个长方体的1排是6cm³，现在有这样的5排，是5个6cm³，因此长方体的体积是5×6=30cm³：又因为1cm³的边长是1厘米，1排是5cm³，因此长方体的长6厘米；现在有这样的5排，因此宽是5厘米，高是1厘米。

教师要求学生以小组为单位搭长方体(如右图)。学生在交流时，教师可适时介入：这个长方体的长、宽、高分别是多少?为什么?这个长方体的体积是多少?为什么?学生通过搭、观察知道这个长方体1排是6cm³，现有这样的5排，是5个6cm³，因此一层是5×6=30cm³；因为现有这样的4层，所以这个长方体体积是6x5x4=120cm³，或者说含有6×5×4=120个1cm³。又因为1cm³的边长是1厘米，1排是6cm³，因此长6厘米；现有这样的5排，因此宽是5厘米，有这样的4层，因此高是4厘米。

接着，教师出示一个被墨水盖住的长方体形(如右图)，并问：现在，谁知道它的体积是多少cm³?为什么?学生已有数长方体体积的经验和表象能力，看到最后1行是7格就知道有7cm³；从右面看有6格，就知道1层有6行，则体积是7×6＝42cm³；看到高有5格，就知道它有5层，则体积是7×6×5=210cm³。教师追问：那么，它的长、宽、高是几厘米?为什么?学生看到1行有7格就知道长是7厘米，因为每格的边长是1厘米；看到有这样的6行就知道它的宽是6厘米，看到有这样的5层就知道它的高是5厘米。

然后，教师继续出示下面两个长方体，并要求学生说说它们的体积分别是多少?为什么?(单位：cm³)

这时，学生的空间能力得到进一步发展。看到长是6小格，就是6厘米，说明长方体1行有6cm³；宽是3小格，就是3厘米，说明有这样的3行，因此长方体1层有6×3=18cm³；现在，这个长方体的高有3小格，是3厘米，就是有这样的3层，所以这个长方体的体积是6×3×3=54cm³。

右上图长方体的长6厘米，说明1行有6cm³；宽4厘米，说明有这样的4行，因此长方体1层有6×4=24cm³：现在这个长方体的高5厘米，说明有这样的5层，所以这个长方体的体积是6×4×5=120cm³。

最后，教师要求学生议一议，并归纳出直接计量长方体体积的方法：长方体体积=长×宽×高。