“运算定律与简便计算”教材解读
徐水琴
人民教育出版社出版的义务教育课程标准四下实验教材,是以整套实验教材的编写思想、编写原则为指导,力求使教材的结构符合数育学、心理学的原理和学生的年龄特征,教材的编写内容具有关注学生的经验与体验,体现知识的形成过程,鼓励算法及解决问题的策略多样化,改变学生的学习方式,体现开放性的教学方法等特点。其中,“运算定律与简便计算”这部分教材的编写就很好地体现了这样的编写意图。
这部分教材在编排上具有以下几个主要特点。
1.有关运算定律的知识相对集中,有利于学生形成比较完整的认知结构
这部分教材的主要内容是加法、乘法的交换律与结合律,乘法对于加法的分配律,以及这五条运算定律的一些比较简单的运用。
加法和乘法的这五条运算定律,不仅适用于整数的加法和乘法,也适用于有理数的加法和乘法。随着数的范围的进一步扩展,在实数甚至复数的加法和乘法中,它们仍然成立。因此,这五条运算定律在“数与代数”领域中具有重要的地位和作用,被誉为“数学大厦的基石”。
学生在前面的学习中,已经接触到了反映这五条运算定律的大量例子,特别是对于加法、乘法的可交换性、可结合性,这些经验构成了学生学习这部分知识的认知基础。因此,将这五条运算定律及其应用集中于一个单元,加以系统编排,便于学生感悟知识之间的内在联系与区别,有利于学生通过系统学习,构建比较完整的知识结构。
教材的编写分为三小节,内容结构如下:
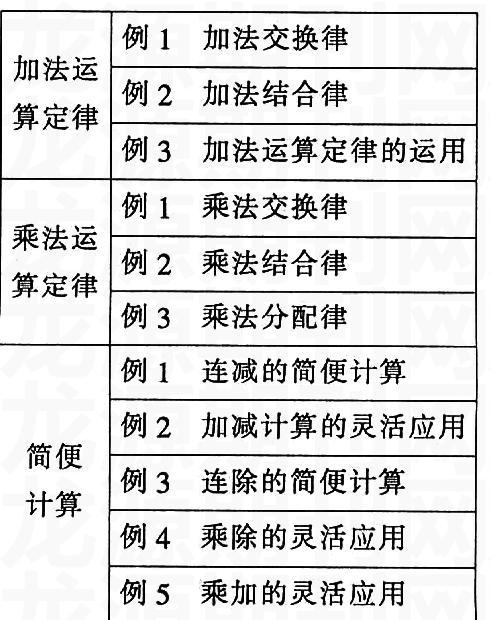
2.从现实的问题情境中抽象概括出运算定律,便于学生理解和应用
这部分教材的一个鲜明特点是,不再仅仅给出一些数值计算的实例,让学生通过计算发现规律,而是结合学生熟悉的问题情境,帮助学生体会运算定律的现实背景。
如加法运算定律,教材从李叔叔骑自行车旅行的情境引出三道例题,分别求李叔叔上下午的路程和、前三天的路程和、后四天的路程和,为学生提供了概括加法交换律和结合律及其应用的具体事例。进一步,再让学生自己举例,并叙述所发现的规律。然后让学生用自己喜欢的方法表示规律,而不是像过去那样,统一用字母来表示。这样编排,一方面有利于符号感的培养,且方便记忆;另一方面提高了知识的抽象概括程度,也为以后正式教学用字母表示数打下初步的基础。
乘法运算定律则以学生参加植树活动的情境为载体设置主题图,由图引出三道例题,为概括乘法交换律、结合律和分配律提供具体的事例。三个例题在教学内容的处理上与教学加法运算定律的两个例题类似。这样编排,能使学生在解决问题的同时,发现、感悟、描述规律。
同时,教材在练习中还安排了一些实际问题,让学生借助解决实际问题,进一步体会和认识运算定律。例如,练习六中的第3题和第4题是乘法运算定律在生活中的实际运用。第4题除了文字提供的信息外,还要引导学生从图中获得解决问题所必需的信息,即新教学楼有4层,再引导学生思考怎样算比较简便。第3题,可以用50×2先算一个来回游了多少米,再乘7;第4题先算25×4(可解释为4层,每层各取一个教室需配多少套课桌椅)再乘7。从而使学生初步体会运算定律在现实生活中的实际意义。
3.重视简便计算在现实生活中的灵活应用,有利于提高学生解决实际问题的能力
在理解和掌握了五条运算定律的基础上,教材安排了进一步学习整数四则运算中的一些简便计算。值得一提的是,教材改变了以往简便计算以介绍算法技巧为主的倾向,着力引导学生将简便计算应用于解决现实生活中的实际问题,同时注意解决问题策略的多样化。这对发展学生思维的灵活性,提高学生分析问题、解决问题的能力,都有一定的促进作用。
教材一共安排了五道例题。例1和例2讨论加减法运算中常用的简便计算,例3和例4讨论乘除法运算中常用的简便计算,例5主要讨论乘、加运算中常用的简便计算。也就是说,例1至例4只涉及同级运算,例5则涉及两级运算。
在这五道例题中,例1和例3讨论的连减、连除运算中的简便计算,过去的小学数学教材中也有同样的内容。新教材主要着眼于通过不同解法的比较,使学生认识一个数连续减去或除以两个数,可以改为减去两个数的和或除以两个数的积,还可以交换两个减数或两个除数的位置再减或再除。
如:172-56-72=172-72-56=100-56=44
172-56-44=172-(56+44)=172-100=72
560÷35÷8=560÷8÷35=70÷35=2
700÷25÷4=700÷(25×4)=700÷100=7
即 a-b-c=a-c-b a÷b÷c=a÷c÷b
=a-(b+c)=a÷(b×c)
教材并没有把它们概括为减法的运算性质或除法的运算性质。在具体的教学中,学生受加法交换律、结合律和乘法交换律、结合律的启发,用知识迁移的方法把它们概括为连减的交换律和结合律,连除的交换律和结合律。为了鼓励学生这种主动学习、主动探究的意识,我肯定了学生的这些想法,同时告诉学生这其实是减法和除法的两个运算性质。
相对而言,其他三道例题的问题情境较为新颖,解决问题的策略较为灵活,在过去的小学数学教材中比较少见。如,例2设计的“书店的一角”。题中包含两个问题:(1)价钱分别为56元、31元、19元、24元的四本书中,哪三本的总价在100元左右?(2)付100元,买48元、47元的书各一套,应找回多少钱?显然,这是两个需要综合应用加减计算的实际问题,而且解决问题的策略具有较大的灵活性。问题(1),教材提示了两种算法。一种是把每三本书的价钱相加。采用这种方法,学生遇到的困难是,四本书取三本书共有几种情况?这是一个组合问题,回答这个问题,如果直接从四本书中每次取三本,要做到不重不漏,思考难度较大。如果反过来思考,四本书中取三本,也就是从四本书中每次去掉一本,就很容易得出共有四种情况。这种反过来思考的间接思路,用于计算三本书的总价,就是教材提示的第二种算法。问题(2),学生容易想到的算法是连减或减去两个价钱的和。因此,教材只提示了第三种另辟蹊径的方法,把100分成两个50。由于两套书的价钱都略小于50,所以这种方法显得比较简便、巧妙。
例5设计的是几位科学家在野外考察的情景图。图下有3~7月份的月历,并标出了科考队的出发日期、计划返回日期和实际返回日期,然后提出问题“科考队这次考察一共花了多少时间”?教材介绍了按月计算和按周期计算两种思路,以及相应的列式计算过程。按月计算的算式是31×2+30×2+26,按周计算的算法是7×21+26,在按月计算的过程中,运用了乘法分配律。然后通过小精灵,鼓励学生提出自己的算法,和同学交流。学生容易想到的是按月计算的思路,根据已知的出发、返回时间,可以知道整个3、4、5、6月都在外面,7月有26天在外。要注意的是3至6月中有两个大月(有31天的月)、有两个小月(有30天的月)。学生列出的算式可能有以下几种,如:31+30+31+30+26、30×4+2+26、31×3+30×2-5、30×5+3-5、31×5-7……只要是对的,都应当给予肯定。按周计算的思路不难理解,但计数一共有多少周比较容易出错。可以让同桌互相指着月历边点边数,也可以请能正确计数的同学介绍自己是怎样数的。

