《展开与折叠》教学案例

刘志芳　马玉兰

1教学目标

(1)让学生经历展开与折叠等操作性活动，在活动中积累必要的数学活动经验，以发展自身的空间观念。

(2)了解正方体(棱柱)的展开图形状，并探索形成不同展开图的途径。

2设计意图

这节课被设计成四大板块，每个板块互相联系、相辅相成，前面为后面做铺垫，后面对前面做进一步的补充。试图在这样紧凑的环节中，大胆放手让学生自己去探索、发现、总结并交流，从中学习知识、掌握方法、发展能力。同时，在探索过程中发展学生的空间观念，并希望他们在学习过程中对数学有一个全新的认识，逐渐喜爱数学活动。

特别地，在教学过程中提供教师和学生、学生和学生平等交流合作的空间。可以将班级中的桌椅摆设成“围坐式”——5人一组，45人共9组，桌面形式如图1。

学生对面而坐，遇到问题很容易互相讨论起来。他们互相启发、取长补短，选择合适的策略，改善自己的思维方式，从而获得成功的体验。这种形式在本节课上发挥了很好的作用，特别是第四个环节中对剪开7条棱这个问题。学生们都积极地参与讨论，有的学生还争论起来。这样的氛围使学生逐步地学会与他人合作交流，并能不断丰富解决问题的策略，提高解决问题的能力。

3教学过程

(1)回顾旧课与引入新课。以下面的问题1作为对上节课的回顾和对本节课的引入。

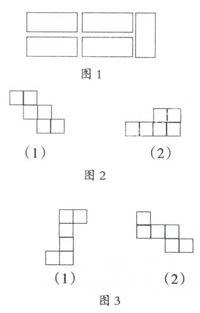
问题1：图2中的图形经过折叠能否成为一个立方体?

在解决这个问题的过程中，引导学生思考：是不是任何一个图形都能折成一个正方体?学生一定会给出否定的回答。继续设问：图2一(2)怎样变化一下就能成为正方体了?学生根据上节课的知识很快就可以解决问题。

在这个活动过程中，学生根据已有的经验体会由面到体的变化特点，并为本节课学习由体到面的变化做了准备。

(2)从具体的操作性活动人手，逐步向空间想象性活动发展。让学生拿出推名好的彩色，正方体，解决下面的问题2。

问题2：你能设法得到哪些平面图形?与同伴交流。

让学生以自己所能够做到的任何方式，沿着棱将正方体剪开展成一个平面图形，并将各自得到的图形贴到黑板上(重复的图不再人选)。

有这样展示自己的机会，学生们的情绪高涨起来，他们认真地操作，争先恐后地将自己的劳动成果贴到黑板上。不一会儿，十几种五颜六色、不同类型的展开图覆盖了整个黑板。学生们看着自己的劳动成果，不禁赞叹起来。这时，教师可抓住时机提出问题：为什么同样的正方体能展成这么多种平面展开图?学生交流各自的展开过程，想象与理解别人的展开方式。再通过七嘴八舌的讨论，最后统一了认识：“是因为剪开方式不同，才出现不同的结果。”建立在操作基础之上的想像力得到了发展。

教师可不失时机地继续引导：以后遇到问题时，不妨从不同的角度多思考几种解决问题的方法，从中选出适合的方法，以便顺利地解决问题。学生非常认同这个观点，从他们的神态中能看出他们对数学有了更进一步的认识。

(3)在头脑里进行“展开”与“折叠”活动。有了前面的动手操作打基础，就可以解决下面的问题3了。

问题3：你能设法把一个正方体展成下面两个给定的图形吗?先想一想，再试一试。

若把前面的两个板块比喻作“自由创意”，这个就是“来料加工”了，特别是要求先在头脑里“想一想”。凭想象来操作图形。难度有所增加。

首先让学生观察图3－(1)中最上面的两个正方形，试图发现其中的特征：右边一个有三条边被剪开，左边一个和右边的相连并被剪开两条边。若能剪出这两个正方形，剩下的也许就容易得到了。这个过程要求学生把立体图形和平面图形结合起来，通过手和脑的协调操作，实现由体到面的转化，进一步发展了他们的空间想像力。图3－(2)看起来和图3－(1)不同，但很快就有学生发现：若把图3－(2)按逆时针方向旋转90°，得到的新图形和图3－(1)前半部分是一样的，至于后面的一些小变化，则一定能解决。这是将新的问题通过转化，并利用已学过的知识解决问题的思维方式，它是一种很好的解决问题的方法，应该在课堂教学中逐渐渗透。(4)拓展。由于上述教学环节的实施比较顺利，所以及时地增加了本环节。这个环节是针对问题4设计的，它属于“拓展”性的问题，转而思考在展开过程中共剪开几条棱。

问题4：将—个正方体的表面沿某些棱剪开。展成一个平面图形，至多可以剪几条棱，至少需要剪几条棱?

回顾自己展开图形的过程，学生很容易数出共剪开7条棱，与同伴交流也得到相同的结果。总是剪开7条棱吗?会不会是偶然?这是本节的难点。经过一段时间的争论，学生发现展开图中的6个正方形必须由5条棱连接着。每两个正方形共1条边，而且多1条棱也不行，那样就不能展开在一个平面上了。而每个正方体有12条棱(12-5=7)，所以总是剪开7条棱。这种解释得到了广泛的赞同。

教师可以继续设问：还有其他的解释方法吗?由于难度较大，学生没有找到答案，最后由教师做了解释：因为剪开1条棱得到2条正方形的边，每一幅展开图的外部都有14条正方形的边(14÷2=7)，所以共剪开7条棱。

本节课是学生发展自身空间观念的一个重要环节，教师将学习的重心放在让学生经历相关数学知识的形成与应用的过程上，并根据学生的年龄特征和已有的数学活动经验(空间图形方面)，设立了“从操作到想象”，再“由操作印证想象”的教学进程，使学生能够更好地理解相关数学知识的意义，切实发展学生的空间想像力。

同时，在教学过程中鼓励学生主动地从事观察、实验、猜测、验证、推理与交流等活动。如让学生亲自动手将正方体剪成平面图形，体会体与面的转变，主动探索其中的数学现象；通过交流了解不同的思考途径所带来的新的认识。更进一步，适时引导学生总结获得知识规律、解决问题的方法，并将它们上升到方法论的层面，如从不同角度思考问题的思维方式等。