初中数学中最短路线的解法举隅

黄明梧

在初中数学中,有一类问题是求按满足某些特定条件连结,使所连结的线段的长度之和最小,称之为最短路线.我们知道,连结两点之间所有的线中,线段最短.本文通过一些例子,介绍一些求最短路线问题的方法.

一、利用轴对称的性质

【例1】 如图1,要在燃气管道l上修建一个泵站,分别向两镇A,B供气.泵站修在管道的什么地方,可以使所用的输气管线最短?

已知:直线l和l的同侧两点〢﹑B.求作:直线l上一点C,且使AC+BC最小.

作法:1.作A关于直线l的对称点A′;

2.连结A′B交直线l于点C.

点C就是所求的点.

证明:略.

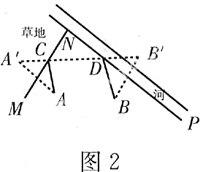
【例2】 如图2,A为马厩,B为帐篷,牧马人某一天要从马厩牵出马,先到草地某一处牧马,再到河边饮马,然后回到帐篷,请你帮他确定这一天的最短路线.

已知:如图2,直线MN、NP及点A、B.

求作:点C在直线MN上,点D在直线NP上,使AC+CD+DB最小.

作法:1.作A关于直线MN的对称点A′,B关于直线NP的对称点B′;

2.连结A′B′交直线MN于点C,交直线NP于点D.点C,D就是所求的点;

3.连结AC,DB.折线ACDB为牧马人这一天的最短路线.

证明:略.

二、利用平移变换的性质

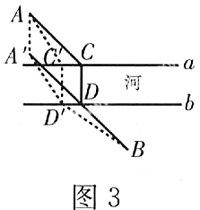
【例3】 如图3,A和B两地在一条河的两岸,现要在河上造一座桥CD.桥造在何处才能使从A到B的路径ACDB最短?(假定河的两岸是平行的直线,桥要与河垂直.)

已知:如图3,直线a∥b,点A,B分别在直线a,b外侧.

求作:点C在直线a上,点D在直线b上,并且CD⊥a,使AC+CD+DB最小.

作法:1.在直线a上任取点C′作C′D′⊥a,交直线b于D′;

2.平移C′D′到AA′;

3.连结A′B交直线b于点D;

4.过点D作CD⊥a,垂足为C;

5.连结AC.

点C,D就是所求的点.CD为建桥位置.

证明:略.

三、利用旋转变换的性质

【例4】 如图4,已知:△ABC.求作:点P,使点P在△ABC内,且点P到△ABC三个顶点的距离之和最小.

作法:1.把AB绕点B逆时针方向旋转60°到BM,把AC绕点C顺时针方向旋转60°到CN;

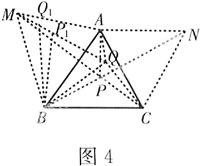
2.连结BN,CM交于点P.

点P就是所求的点.

证明:设点Q是△ABC内异于点P的任意一点,连结AQ,BQ,CQ,把△ABQ绕点B逆时针方向旋转60°到△MBQ₁,由旋转变换的性质知:Q₁M=QA,Q₁B=QB,∠Q₁BQ=60°

∴△Q₁BQ是等边三角形.

∴QQ₁=BQ.

∴AQ+BQ+CQ=MQ₁+QQ₁+QC,

连结AM,AN则

∵AB=MB,∠ABM=60°;AC=AN,∠ACN=60°,

∴△ABM,△CAN均为等边三角形.

∴AM=AB,∠BAM=60°,AN=AC,∠CAN=60°,

∴△ABN是由△AMC绕A顺时针方向旋转60°而得.

∴∠MPB=60°.

连结AQ,在PM上截取PP₁=BP,则△PP₁B是等边三角形.

∴BP=BP₁,∠P₁BP=60°,

∵AB=MB,∠ABM=60°,

∴△MBP₁是由△ABP绕B顺时针方向旋转60°而得.

∴MP₁=AP.

∴PA+PB+PC=MP₁+P₁P+PC=MC.

∵MC1