浅谈初中数学教学中思维能力的培养

杜祖相

培养学生良好的思维方法和思维习惯是数学教学的终极目标，而提出问题是思维创新的源泉，提出问题的能力应该是现代中学生必须具有的能力之一。问题意识的产生是学生提出问题的前提，教师通过设计问题情境来激发学生的兴趣，通过对学生进行思维训练来培养学生的怀疑精神。

（1）发散性思维的培养。在初中数学教学中，特别是几何，三角函数变换等，想象力显得犹为重要，它是解决许多数学问题的基础。

比如有这样一道题目：讲的是矩形折叠问题，在矩形ＡＢＣＤ中，ＡＢ＝6ｃｍ，ＢＣ＝8ｃｍ将矩形折叠，使点Ｂ与点Ｄ重合，求折痕ＥＦ的长是多少？

同学们采用四种不同的方法：

①用相似三角形；②用平行移动；③用三角函数定义；④利用面积；此题的目的是通过学生一题多解，启发学生的发散性思维，从而提高了学生的综合解题能力。

对处在学习能力一般的学生我鼓励他们克服学习上的困难，在学习过程中以扎实掌握课本基础知识为主，学会灵活综合运用各种知识，立足课本，适当补充，注重审题、思路、规律、答题技巧。

又比如我在讲二次函数与Ｘ轴的两个交点和一元二次方程的两个根的联系与区别时采用了对比法，让同学很容易理解两者的区别。

二次函数与Ｘ轴的两个交点

一元二次方程的两个根

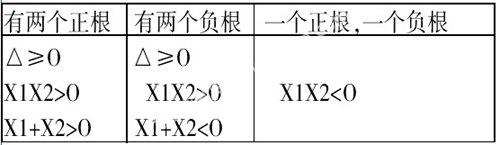
当在讲这道题目时，很多同学就问到了第三种情况怎么不考虑判别式。其实在Ｘ1Ｘ2＜Ｏ，中已经考虑了判别式大于零了。

对于学习能力较差的学生对教师的依赖性最大，因此要注意利用各种机会激发学习兴趣，在教学过程中注重培养学生养成独立思考的习惯，帮助学生逐步学会怎样理解所学知识、如何掌握与其他知识的联系；在实践环节上加强“双基”的演练。

这一层次的学生感到最难的就是繁多的公式定理，学生记不牢，也就用不好，而单纯地死记硬背，又往往容易记错。我就对某些公式加以概括提炼，编一些形象易记的口诀，学生会很感兴趣，乐于接受，记忆牢固，会收到事半功倍的效果。

如平移问题，我归纳成八个字：“上加下减，左加右减”。

又如在一些几何题目当中经常碰到这样的两个条件“一个是平行线，一个是角平分线”。学生取了其中的两个“平”字，把它简称为“双平法”，很形象生动。以后遇见这种题目同学们很容易想到该怎样去做，很快就能变繁为简，变难为易。

（2）思维深刻性的培养。初中阶段教学应着重发展学生的逻辑思维，适度发展严谨性，扩展思维的深度，提倡从整体角度思考问题，使思维深刻性的发展和培养取得较为理想的效果。

思维的逻辑一般表现在思维过程中依据一定的逻辑关系、逻辑规律，对问题和现象进行观察、抽象、判断、推理以更快更简捷的解决问题。在教学中，教师一方面通过例题讲解，穿插问题的逻辑关系和逻辑规律，另一方面鼓励学生多动手，对定理、公式自己推导。逐步掌握思维的逻辑规律，形成有步骤、有规律、有层次思维的良好模式。

初中学生由于受认知水平和心理特征等因素的限制，思维的严谨性水平一般都不高。丢三落四，思维混乱，忽视定理公式的成立条件而滥用定理公式。因此，思维的严谨性相当重要。主要的训练方法有：①严格审查题目条件，定理公式的条件范围是否满足；②要学会用数学语言表达所思所想；③在证明推理过程中，做到每一步都有理有据。

思维的逻辑性、思维的严谨性是相互影响相互联系的。在教学过程中，要适度进行综合与渗透，不断提高学生对问题现象的归纳、概括和抽象能力。如在平面和立体几何中，应该通过训练使学生的解题思路清晰、语言规范、阐述完整，还应该让学生从多角度思考问题，找到最简单的解题方法。逐渐使学生的思维趋于严谨、深刻。

思维能力的培养是上述多个方面综合培养训练的结果。初中阶段的培养是思维的基础阶段，应重点抓住基础思维品质的发展和培养，分清主次，明确目标，协调发展。这样，才能形成学生良好的思维品质，为更高一级阶段的学习打下良好的基础。