直观教学不能只讲直观

陈新福

在教学六年级圆柱和圆锥的认识中，安排有这样一道习题：有一个长方体木料，长是40厘米，宽是20厘米，高是30厘米。将这块长方体切割成一个最大的圆柱，求这个圆柱的体积是多少立方厘米?

结果很多的学生无从下手，感到比较困难。于是，我决定用直观教具进行演示，帮助学生形成解决该问题的思考方法与策略。

教学思路形成后，我马上用萝卜削了3个长方体，分别对这3个长方体削成圆柱体后的三种情况一一进行演示图示如下：

从操作可知：

图1中圆柱体的底面半径是10厘米，体积计算算式是：3.14*10²*30

图2中圆柱体的底面半径是15厘米，体积计算算式是：3.14x15²x20

图3中圆柱体的底面半径是10厘米，体积计算算式是：3.14x10²*40

最后得出图2中所削成的圆柱体的体积最大。

事隔一周，中途没有让学生进行相关习题的练习，我们对全班55人进行了类似题目的测试，题目是：有一个长方体木料，长是50厘米。宽是40厘米，高是30厘米，将这个长方体切割成一个最大的圆柱，求这个最大圆柱的体积是多少立方厘米?测试后对学生的学习情况进行了统计。结果如下表：

本以为通过直观操作演示，学生对该习题的解决方法、策略会有比较深刻的理解，初步估计学生再次解决该类题目的成功率会在90％左右，结果却出乎我的预料，成功率只有50％左右，这是为什么呢?经过对教学的反思及学生错题的分析，我们认为整个教学存在以下缺失。

一、教具直观与函象直观(脑图)有效结合不够

回忆前面进行的教学，我们发现教师是通过三个教具的直观演示；获得每个圆柱体的计算条件。然后进行列式。这样的环节设计，学生确实已经理解了这道题目，但是不具备解决同类问题的能力，因为学生没有对实物进行有效思考，“进入”大脑。我们认为以上三种情况可以这样处理：图1通过实物操作，图2、图3则先不出现实物：而是引导学生进行思考：这个长方体还可以怎么摆，怎样削能使它成为圆柱体?思考后请你把自己的想法画个草图。接着教师根据学生的回答，再对比教具，让学生对照自己的草图，修改芋图；通过“一想、二画、三对照、四修改”，促使学生将外在之物内化到头脑里，让学生把长方体放到头脑中进行“切割”形成“脑图。”

二、在整体感知条件的基础上，通过有序思考“线韵条件”促进学生建立“脑图”

通过以上分析我们知道学生是否形成“脑图”是学习的关键所在，而有效建立“脑图”则需要有序思考。通过分析我们知道点、面对长方体摆放图的思考不具有直接的指示性，而从“线”人手，思考“谁是长方体的高?”，则能使我们的思考做到有序、有效。设长方体的长、宽、高分别是a、b、c，我们从“谁是高”来思考就能清楚地知道有三种情况：

第一幅图的高是a，那么底面的两条边就是b与c；

第二幅图的高是b。那么底面的两条边就是a与c；

第三幅图的高是c，那么底面的两条边就是a与b。

当“高”这个条件确定后，接着就可以从底面的长与宽这两个条件入手，以宽的长度的一半作为半径来列式计算。

三、开展错式与图的对比分析，能有效提升学生的解题能力

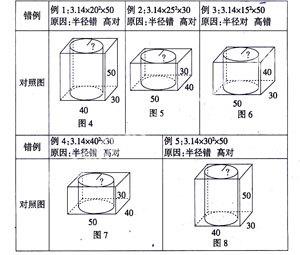
通过学生再次练习的错误列式统计，我们发现学生的错误主要是“脑图”没有很好地建立；另外，由于没有对图的充分认识，也就没有认清切割后圆柱体的底面半径与高的对应关系，这也是解题出错的重要因素。以再测试的题目为例，我们将学生的错误列式与图对照分析如下：

以此，学生可以清楚地知道：当圆柱体的“高”确定后，圆柱“底面半径”的确定就成为解题的关键所在，“底面半径”就是底面长与宽这两个数据中较小数据的一半。

通过一道几何计算河题教学的实践与思考，我们认为：直观操作必须要与学生头脑中的“脑图”建立相结合。思维展开时可以把“体”转化成“体”当中的“线”作为思考对象，这样将使我们的思考更有序，表达更清晰。解题结束后，还应该将学生学习中的错误解答与图作明确的对照分析，做好“两个对应”：即计算公式与数值条件的对应。数值选择与图的对应，切实突破学习中的难点，促进学生更为主动，有效地学习数学。

责任编辑：陈国庆