带尖角的障碍声波散射区域的反演
张梅东,王连堂
(1.防灾科技学院基础部,河北燕郊 065201;2.西北大学数学系,陕西西安 710127)
带尖角的障碍声波散射区域的反演
张梅东1,王连堂2
(1.防灾科技学院基础部,河北燕郊 065201;2.西北大学数学系,陕西西安 710127)
对带尖角的障碍声波散射区域进行了反演,其前提条件是整体场满足奇次Dirichlet边界条件.在用Nystr¨om方法解正问题的过程中,由于采用等距网格积分给尖角处带来很差的收敛性,这是因为双层位势的积分算子的核在尖角处有Mellin型奇性,不再是紧算子;为此采用梯度网格,数值例子表明该处理方法的有效可靠性.
尖角;反演;Dirichlet边界条件;Nystr¨om方法
1 引言
声波反散射理论是近十多年才发展起来的数学物理理论,在这方面已有大量的研究,特别是文[1-3]等利用积分方程方法对反散射问题作了深刻的研究,得到了一些漂亮的结果.对声波散射区域的重建,大都限于较规则的区域,但对不太好的区域、如非凸区域,有角点的区域研究较少,因为有效的重建对未知区域边界的光滑性要求较高.本文所讨论的问题就是对带尖角区域的重建,在本文中用单双层位势的修正来逼近散射波(1.6式,1.8式),这种修正对用Nystr¨om方法解决问题时的误差分析很有效,即使在尖点处的跳跃关系的余项不会发生变化,因为首项的密度在尖点处的奇性消失.然而积分方程的核在尖点处不再是弱奇性的,不再是紧算子.对此从积分方程中分离出紧算子的部分;对剩余的非紧算子,选择一个连续的截止函数,再对此算子作一变换,从而就能保证剩余的非紧算子在尖点处的某邻域处也是紧的.又由于边界积分方程解的导数在尖角处有奇性,为了更好的处理此奇性,采用梯度网格代替等距网格积分,最简单的办法是用新的变量来生成一个梯度形式,然后再对新的变量等距积分,从而就能保证新的变量的导数直到某一阶数才为零,并且节点的一半就等同于分布在整个区间,而另一半节点都向尖点处聚集,这样使误差大大减小,从而得到了很好的反演效果.

(1.3)式称为Sommerfeld辐射条件,且在所有方向上一致成立.

对问题(1.1)-(1.3)有以下定理:
定理[3]1.1设Im(k)≥0,(1.1)-(1.3)存在唯一解,且相对于最大模范数,解us在R2D上,us的各阶导数在R2¯D的任一闭子集上连续依赖于边界数据.
本文讨论的问题是障碍区域带尖角的,不失一般性,假定尖点在x0处,边界∂D{x0}是C2类分段解析的.并假定尖点处的夹角γ:0<γ<2π,假设在D内部,k2不是负的Laplace算子的Dirichlet特征值,用单双层混合位势的修正逼近散射波us

其中f=−eikx·α,α是入射方向.密度ϕ(x)−ϕ(x0)在尖点处的奇性消失,故在尖点处的跳跃关系的余项不会变化,然而(1.9)式中积分方程的核在尖点处不是弱奇性的,在尖点处算子K(见(2.7)式)不是紧算子.对于一个c2类的边界双层位势算子的核的弱奇性依赖于以下不等式[3]
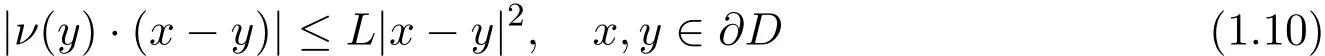
L是常数.然而在尖点的某邻域(1.10)式已无效,为此在尖点处的某邻域分离出算子
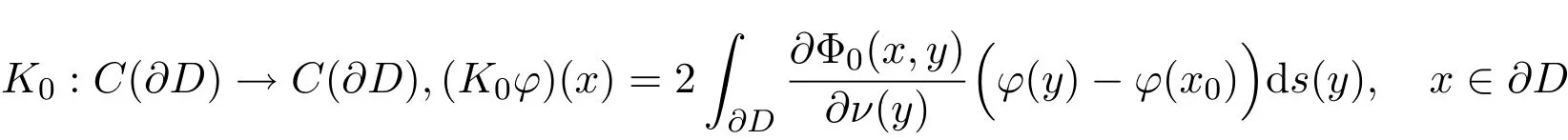
由文[2]知(1.9)式中余下的积分算子是弱奇性的紧算子.算子K0不是紧的.要做以下处理:选择充分小的适当的正数r>0,作以尖点x0为圆心半径为r的圆.∂D在圆内的两段弧A,B总存在不依赖于r的某个常数L,对所有x,y∈(A∪B){x0}使(1.10)式一致成立[2].为此选择一个连续截断函数
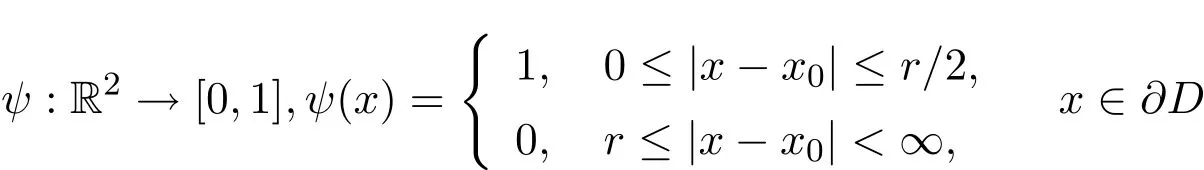
函数w:[0,2π]→[0,2π]是双射且严格单调递增,并无穷可导.其在区间[0,2π]端点处的导数直到某一阶数为零.替换后变量s,σ用Nystr¨om方法进行等距网格积分,选择适当的阶数p∈N(下文数值例子中取p=8),从而得到很好的收敛结果.
2 反演的数学分析

3 收敛性分析

4 数值例子

其中aj,bj见表2,反演效果看图2,正问题数据见表1.
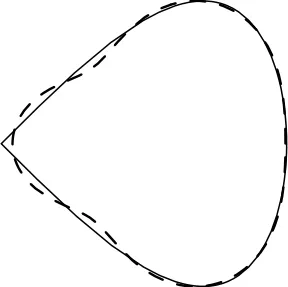
图1 实线表示精确图形;虚线表示反演图形
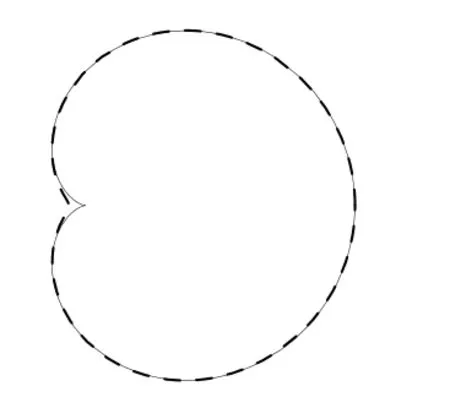
图2 实线表示精确图形;虚线表示反演图形
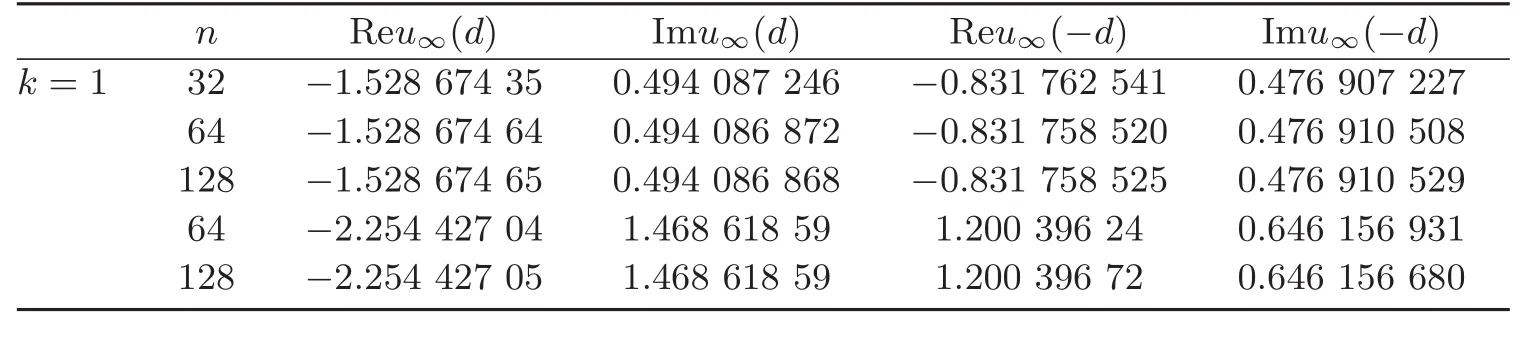
表1 例2的u∞(d)及u∞(−d)
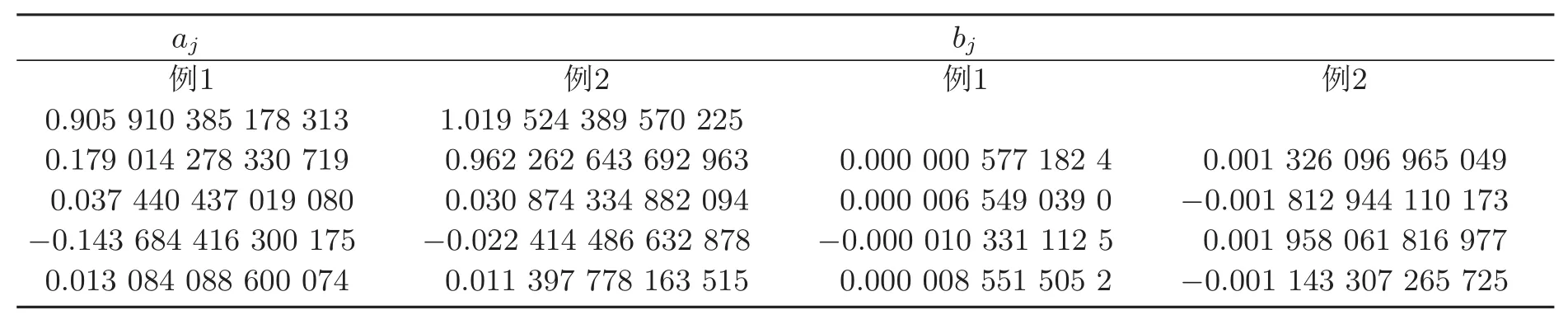
表2 例1及例2中的系数aj,bj
[1]Kress R.Linear Integral Equations[M].Berlin:Spring-Verlag,1989.
[2]Colton D,Kress R.Inverse Acoustic and Electromagnetic Scattering Theory[M].Berlin:Spring-Verlag,1992. [3]Colton D,Kress R.Integral Equation Methods in Scattering Theory[M].New York:Wiley-Interscience Publication,1983.
[4]王连堂.反演声波阻尼系数的一个逼近方法[J].计算数学,2000,22(3):265-274.
[5]王连堂,薛西峰.利用正则化方法求解声波散射问题[J].纯粹数学与应用数学,1998,14(4):11-16.
[6]王连堂.利用散射波的叠加重建声波散射区域[J].应用数学学报,1998,21(3):384-392.
The reconstruction of scattering domain with a corner of
acoustic waves
ZHANG Mei-dong1,WANG Lian-tang2
(1.Department of Basic Courses,Institute of Disaster Prevention Science and Technology,Yanjiao065201, China;2.Department of Mathematics,Northwest University,Xi’an710069,China)
The reconstruction of the scattering domain with a corner of acoustic waves is presented in this paper,it is assumed that the total field satisfied homogenous Dirichlet boundary condition;in direct problem by Nystr¨om,due to the singularity of the solution at the corner,a quadrature method based on an equidistant grid only very poor convergence.The kernel of double−layer integral operator in a domain with a corner has a Mellin type singularity at the corner and no longer is compact in the space of continuous function.Hence graded mesh is used.Numerical examples indicate that this method is accurate and simple to use.
sharped-corner,reconstruction,Dirichlet boundary condition,Nystr¨om method
O241.8
A
1008-5513(2009)03-0610-07
2008-12-20.
张梅东(1975-),硕士,助教,研究方向:数学物理方程反问题.
2000MSC:31A25

