环的Armendariz性

任艳丽,景丽敏,2

(1.南京晓庄学院数学系,江苏南京 210017;2.辽宁师范大学数学系,辽宁大连 116029)

环的Armendariz性

任艳丽1,景丽敏1,2

(1.南京晓庄学院数学系,江苏南京 210017;2.辽宁师范大学数学系,辽宁大连 116029)

研究了一个环何时具有Armendariz性.使用环论的一般方法,证明了在一定条件下商环、具有一对零同态的Morita Context环以及映射环是Armendariz环,推广了已有的某些结果.

Armendariz环;商环;Morita Context环;映射环

1997年文[1]提出了Armendariz环的概念.称环R是Armendariz环,如果

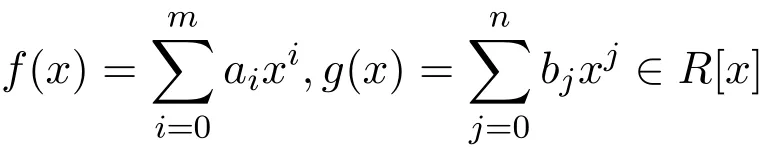
满足f(x)g(x)=0,则有aibj=0(0≤i≤m,0≤j≤n).用Armendariz环命名是因为早在1974年Armendariz就发现了Reduced环(不含非零幂零元的环)满足这个条件.在这之后很多人对Armendariz环进行了讨论和研究,1998年文[2]证明了若R是Armendariz环, 则R[x]也是Armendariz环.文[3]证明了一类商环的Armendariz性.文[4]又讨论了特殊矩阵环的Armendariz性,并给出了R和M的平凡扩张

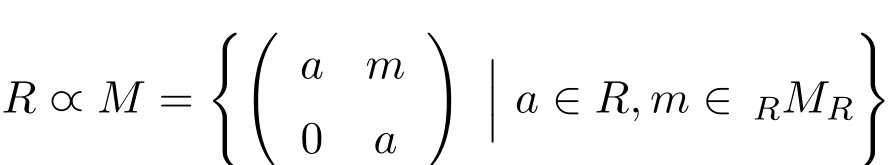
为Armendariz环的充要条件,本文将继续讨论几种环的Armendariz性.文中环R均指有1的结合环.

1 商环

A,B为R的理想,那么A,B的商为(A:B)={x∈R|xB⊆A}[5]

定理1.1设A,B为R的理想,如果R/A为Armendariz环,则R/(A:B)是Armendariz 环.

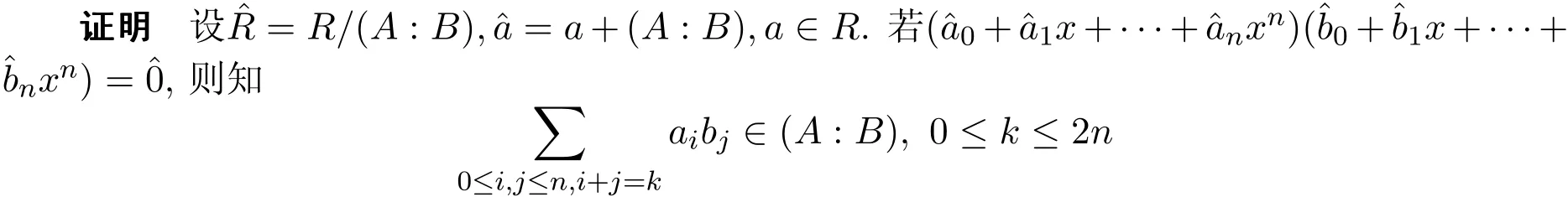
从而对于任意的u∈B,有

由此,我们可以直接得到文[3]引理3.6和文[6]引理1.4.1.

推论1.2设R是Armendariz环,

(1)如果I为R的理想,则R/lR(I)是Armendariz环.

(2)如果Rn={x∈R|nx=0},则R/Rn是Armendariz环

证明(1)lR(I)=(0:I)={x∈R|xI=0},R/(0)=R是Armendariz环.由定理1.1, R/lR(I)=R/(0:I)是Armendariz环.

(2)nR={nx|x∈R}是R的理想.而Rn=(0:nR)={x∈R|x·nR=0}.由定理1.1,R/Rn=R/(0:nR)是Armendariz环.

文[2]给出了当R是Armendariz环,I是R的理想,但R/I不是Armendariz环的例子.由此可知Armendariz环的同态像也不一定是Armendariz环,但是根据以上定理给出下面条件就能使同态保Armendariz性.

推论1.3设R,S是环,f:R→S是R到S上的环同态.如果R是Armendariz环,且存在理想B⊆R,使得其左零化子恰是kerf,则S是Armendariz环.

证明由题设知,存在R的理想B,使得kerf=(0:B)={x∈R|xB=0}.由推论1.2 知,R/kerf=R/(0:B)=R/lR(B)是Armendariz环,0→kerf→R→S→0是正和序列.因此,S≌R/kerf是Armendariz环.

1998年文[2]定义了一个R-模M是Armendariz右R-模,如果

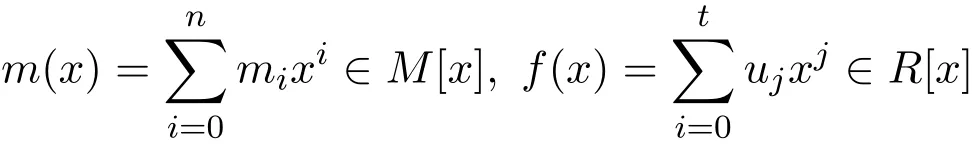
满足m(x)f(x)=0,就有miuj=0(0≤i≤n,0≤j≤t).同样可以定义Armendariz左R-模.与文[6]中两个理想的商定义相似,文[7]给出(N:M)={x∈R|xM⊆N},其中M是左R-模,N是M的R-子模.(0:M)={x∈R|xM=0}=A(M).这样就有

定理1.4设M是Armendariz左R-模,则R/A(M)是Armendariz环.

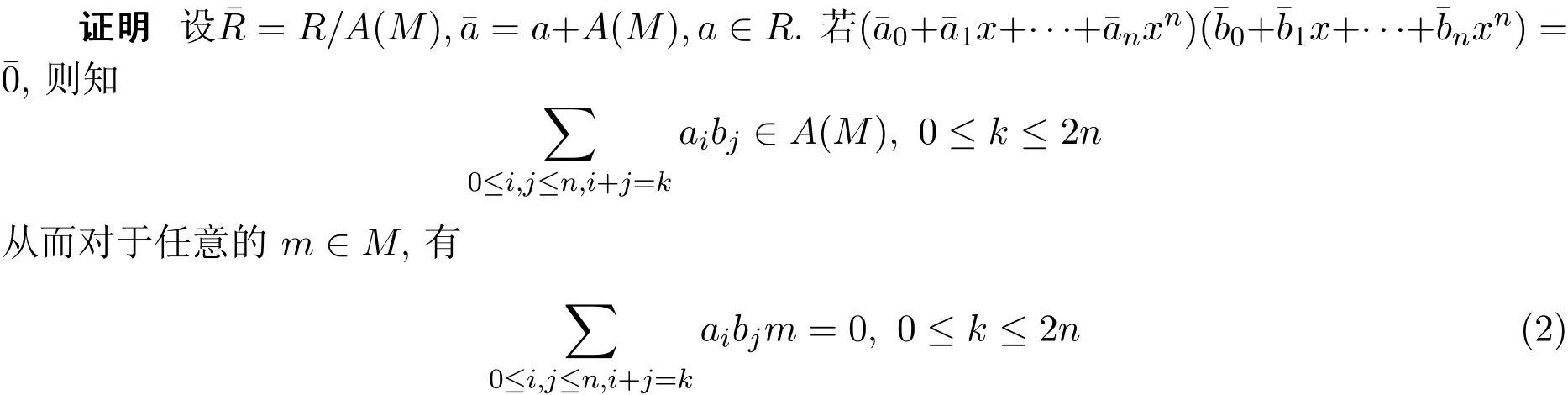
这样就得出了一个环的商环是Armendariz环的外部刻划.推论1.2也可看作此定理的一个推论.

推论1.5环R有一个既约模M是Armendariz左R-模当且仅当环R存在一个极大左理想、正则左理想T,使得R/T是Armendariz环.

证明M是R的既约左R-模,则任意0/=m∈M,T=(0:m)是R的极大左理想,正则左理想,A(M)⊆(0:m).由定理1.4知R/A(M)是Armendariz环,所以R/T=R/(0:m) 是Armendariz环.

反之,设T是R的极大左理想、正则左理想,则存在R既约左模M,m∈M使得T= (0:m),R/T=R/(0:m)是Armendariz环,且M=Rm,所以对任何f(x)=a0+a1x+…+ anxn,g(x)=b0m+b1mx+…+bnmxn=0,f(x)∈R[x],g(x)∈M[x],若f(x)·g(x)=0,则X

2 具有一对零同态的Morita Context环

定理2.2若V是(A,B)-双模,W是(B,A)-双模,那么C是Armendariz环的充要条件是

(1)A,B是Armendariz环;

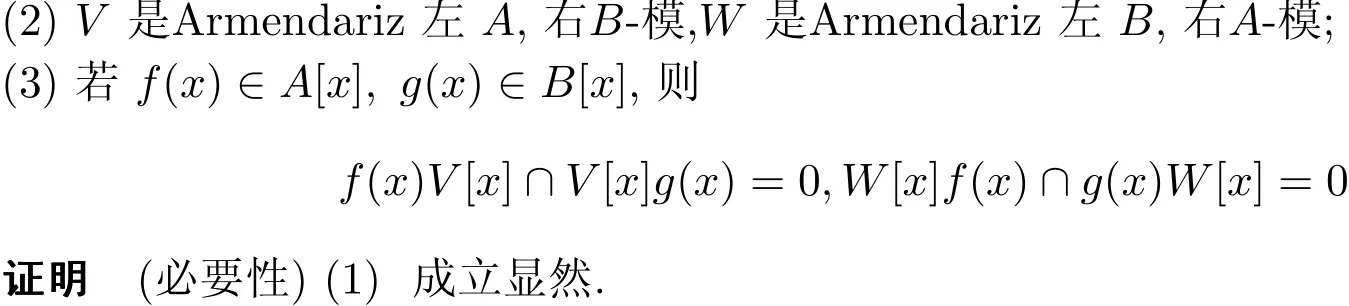
与C[x]是Armendariz环也相矛盾.所以W[x]f(x)∩g(x)W[x]=0.

(充分性)设α(x)β(x)=0,其中

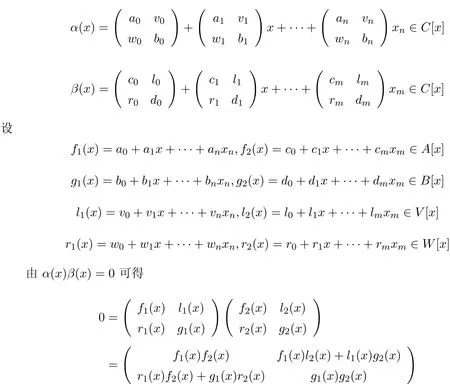
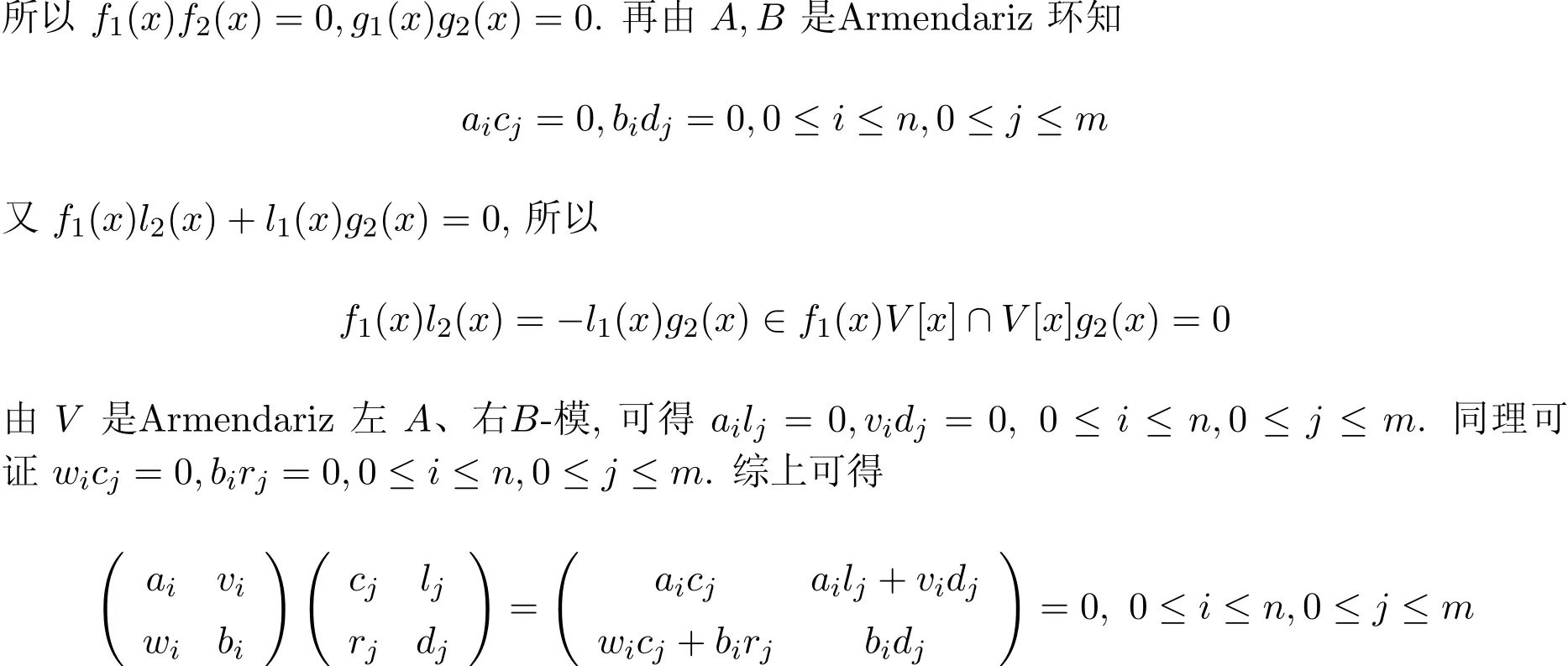
所以C是Armendariz环.

当W=0(V=0)时,C是上(下)形式三角矩阵环,因此这里也给出了形式三角矩阵环是Armendariz环的充要条件,而文[2]定理2.2是此定理的特殊情况.

3 映射环

设S是任意一个环.令A={f|f:S→Z},在A上定义加法、乘法定义为

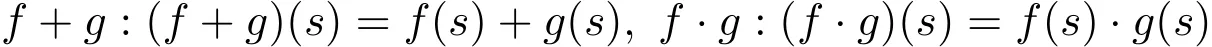
则A构成一个环,称A为Z-整数环.

定理3.1Z-整数环A是Armendariz环.

证明设f(x)=f0+f1x+…+fnxn,g(x)=g0+g1x+…+gnxn∈A[x].如果f(x)·g(x)=0, 则

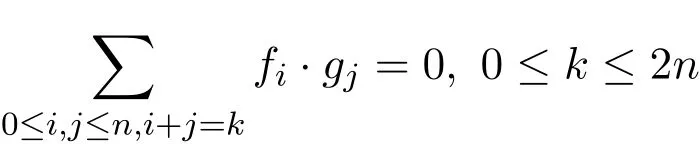
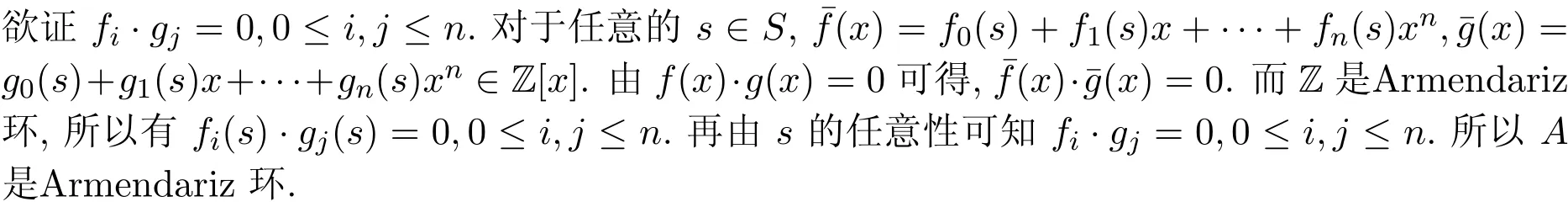
根据Z−整数环可以定义R-环A={f|f:S→R},其加法和乘法定义如上.

推论3.2如果R是Armendariz环,那么R-环A是Armendariz环.

关于一般代数对象(参见文[9])的Armendariz性,我们再另文讨论.

[1]Rege M B,Chhawchharia S.Armendariz rings[J].Proc.Japan.Acad.Ser.A.Math.Sci.,1997,73:14-17.

[2]Anderson D D,Camillo V.Armendariz Rings and Gaussian rings[J].Comm.Algebra,1998,26(7):2265-2272. [3]Lee Tsiu-kwen,Wong Tsai-lien.On Armendariz rings[J].Houston J.Math.,2003,29:583-593.

[4]Lee Tsiu-kwen,Zhou Yi-qiang.Armendariz and reduced rings[J].Comm.Algebra,2004,32(6):2287-2299.

[5]Atiyah M F,Macdonald I G.Introduction to Commutative Algebra[M].Massachusetts:Addison Wesley Publishing Company,1969.

[6]郭颖,杜现昆,谢敬然.Armendariz环和斜Armendariz环[J].吉林大学学报:理学版,2005,43(3):253-257.

[7]刘绍学.环与代数[M].北京:科学出版社,2001.

[8]王尧,任艳丽.具有一对零同态的Morita Context环(I)[J].吉林大学学报:理学版,2006,44(3):310-324.

[9]任艳丽,王尧.一般代数对象的挠理论[J].纯粹数学与应用数学,2002,18(4):338-342.

Armendariz properties of rings

REN Yan-li1,JING Li-min1,2
(1.Department of Mathematics,Nanjing Xiaozhuang University,Nanjing210017,China; 2.Department of Mathematics,Liaoning Normal University,Dalian116029,China)

In this paper,we investigate the conditions that a ring is Armendariz ring,show that quotient rings,Morita Context rings with a pair ofzerohomomorphisms and map rings are Armendariz ring under some conditions by using of general mathods in ring theory,and generalize some results in literatures.

Armendariz ring,quotient ring,Morita Context ring,map ring

O153.3

A

1008-5513(2009)03-0442-06

2008-01-10.

辽宁省教育厅科研基金(05L014).

任艳丽(1965-),硕士,教授.研究方向：一般环论

2000MSC:16W50