二阶椭圆问题新混合元模型的超收敛分析及外推

石东洋,王慧敏,2

(1.郑州大学数学系,河南郑州 450052;2.河南工程学院数理科学系,河南郑州 450007)

二阶椭圆问题新混合元模型的超收敛分析及外推

石东洋1,王慧敏1,2

(1.郑州大学数学系,河南郑州 450052;2.河南工程学院数理科学系,河南郑州 450007)

对二阶椭圆问题通过“增补”办法导出一个新的混合模型.在各向异性网格下,利用积分恒等式技巧得到了真解与ECHL元近似解的超逼近性质.同时基于插值后处理技术导出了整体超收敛.进一步,通过渐进误差展开和分裂外推,得到了比通常的误差估计更高一阶的收敛速度.

新混合模型;各向异性网格;后处理技术;超收敛;误差展开及外推

1 引言

对二阶椭圆问题

令u=▽p,则无论是Babuˇska-Brezzi混合元法[1]还是最小二乘有限元法(FOLS)[2-3],都不可能用L2(Ω)-元素作为u的逼近,通过“增补”办法[4]得到一个新的混合模型,克服了上述缺陷,并给出了收敛性分析.但其要求剖分满足正则性[5](即≤c,这里hK为剖分单元K的直径,ρK为K的最大内切圆直径,c是一个常数).最近的一些研究[6-7]表明,这种假设对一些单元来说是不必要的,且对那些定义在窄边区域上的问题如果用正则性剖分,计算量将非常大而无法承受.这时若利用各向异性网格则可以节约大量的自由度而获得同样的收敛效果.

本文针对这种新的混合模型,讨论了ECHL混合元,并利用积分恒等式技巧得到超逼近性质.同时,通过构造适当的插值后处理算子导出了整体超收敛的结果.更进一步经插值后处理和分裂外推后,与通常的误差估计相比收敛速度提高了一阶.本文的结论不要求网格剖分满足上述正则性条件.

2 二阶椭圆问题及其逼近

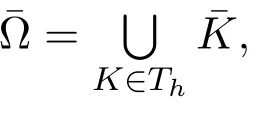
3 基本估计式

4 ECHL元超逼近及超收敛

图1 大单元~K

由文[9]的技巧可以验证上述构造的插值后处理算子J2h具有各向异性特征,即α= (α1,α2),当|α|=1时有

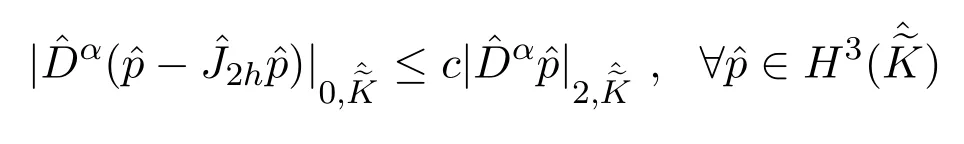
同文[10]可以验证,在上述条件下,对任意u∈(H2(Ω))2,p∈H3(Ω),插值算子I2h,J2h满足

5 ECHL元的外推

为了得到外推的结果,对引理1的(7)式,引理2的(9)式进一步展开.

引理3若p∈H4(Ω),对任意的v∈Vh,则有

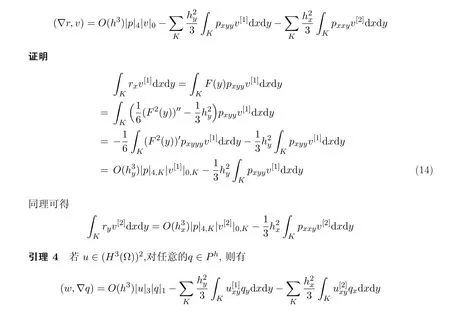
利用文[8]中的思想构造插值算子I3h,J3h,具体做法如下:

把相邻的九个小单元Ki(i=1,2,···,9)合并为一个大单元¯K,定义插值算子I3h,J3h使得在单元¯K上对任意的(u,p),有

其中Ki(i=1,2,···,9),Zj(j=1,2,···,16)分别为小单元及它们的顶点.

由文[9]的技巧可以验证,上述构造的插值后处理算子J3h具有各向异性特征.

同文[10]可以验证,在上述条件下,对任意u∈(H3(Ω))2,p∈H4(Ω),插值算子I3h,J3h满足

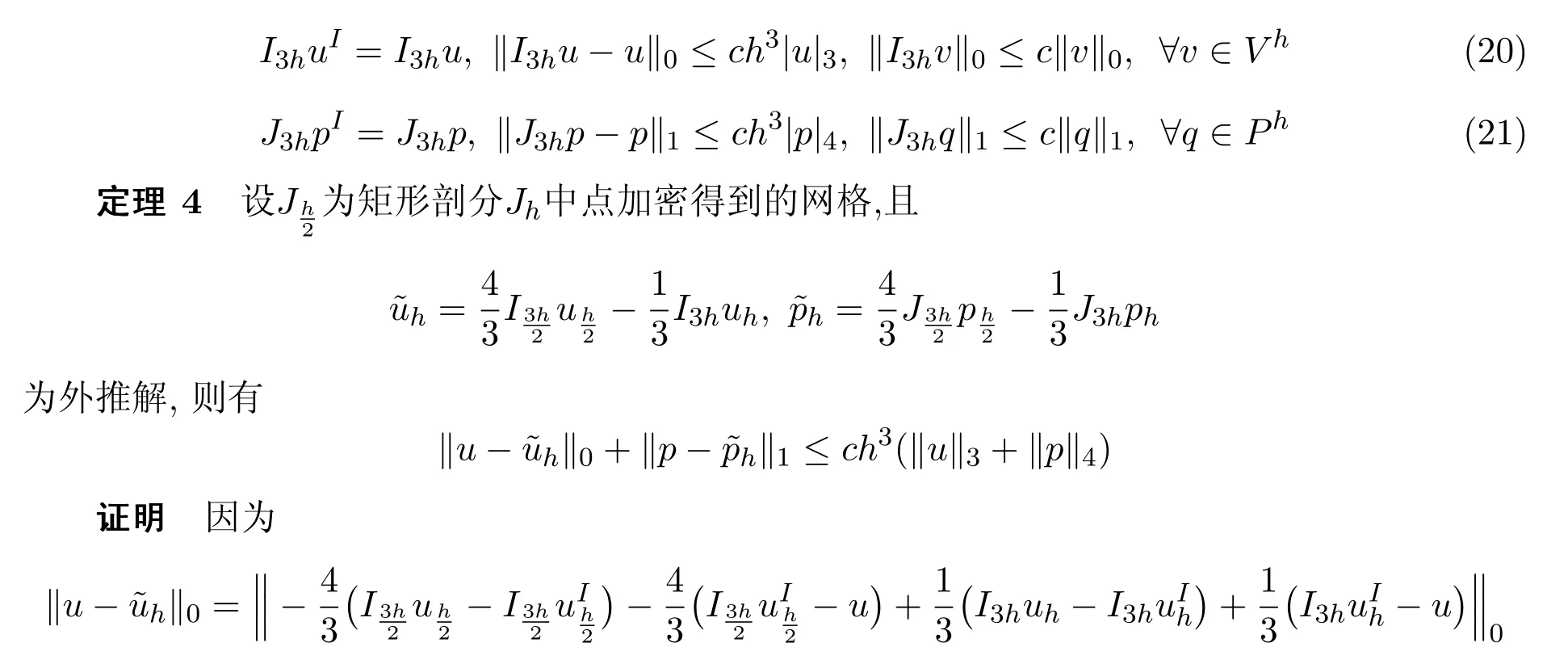
[1]Brezzi F,Fortin M.Mixed and Hybrid Finite Element Methods[M].New York:Springer-Verlag,1991.

[2]Bramble J H,Lazarov R D,Pasciak J E.Least-squares for second-order elliptic problems[J].Comput.Methods Appl.Mech.Engrg.,1998,152:195-210.

[3]Pehlivanov A I,Carey G F,Lazarov R D.Least-squares mixed finite elements for second-order elliptic problems[J].SIAM J.Numer.Math.,1994,31:1368-1375.

[4]段火元,梁国平.二阶椭圆问题的混合元方法[J].计算数学,2001,23(4):417-421.

[5]Ciarlet P G.The Finite Element Method for Flliptic Problem[M].New York:North-Holland,1978.

[6]Zenisek A,Vanmaele M.The interpolation theory for narrow quadrilateral isoparametric finite elements[J]. Numer.Math.,1995,72(1):123-141.

[7]Apel T,Lue G.Anisotropic mesh refinement in stabilized Galerkin methods[J].Numer.Math.,1996,74(3):261-282.

[8]林群,严宁宁.高效有限元构造与分析[M].保定:河北大学出版社,1996.

[9]Chen S C,Shi D Y,Zhao Y C.Anisotropic interpolation and quasi-Wilson element for narrow quadrilateral meshes[J].IMA.J.Numer.Anal.,2004,24:77-95.

[10]石东洋,梁慧.一个新的非常规Hermite型各向异性矩形元的超收敛分析及外推[J].计算数学,2005,27(4):369-382.

Superconvergence analysis and extrapolation of a new mixed finite element model for second order elliptic problem SHI Dong-yang1,WANG Hui-min1,2

(1.Deparment of Mathematics,Zhengzhou University,Zhengzhou450052,China;
2.Department of Mathematics and Physics,Henan Institute of Engineering,Zhengzhou450007,China)

A new mixed finite element model for the second order elliptic problem is presented by supplementing way.The superclose properties of the exact solution and the approximate solution of ECHL element are derived through integral identity technique on anisotropic meshes.At the same time,based on the interpolated postprocessing technique,the global superconvergence is obtained.Furthermore,one order higher convergence rate than the general error estimate is derived using asymptotic error expansion and the extrapolation.

new mixed finite element model,anisotropic meshes,postprocessing technique,superconvergence, error expansion and extrapolation

O242.21

A

1008-5513(2009)04-0630-08

2007-06-08.

国家自然科学基金(10671184).

石东洋(1961-),博士,教授,研究方向：有限元方法及应用.

2000MSC:65N30,65N15