一类非线性演化方程初值问题的幂级数解
朱春蓉,王建强
(1.安徽师范大学数学计算机科学学院,安徽芜湖 241000;2.西北大学数学系,陕西西安 710069)
一类非线性演化方程初值问题的幂级数解
朱春蓉1,2,王建强1
(1.安徽师范大学数学计算机科学学院,安徽芜湖 241000;2.西北大学数学系,陕西西安 710069)
研究了一类非线性演化方程初值问题.通过不变子空间方法,这类初值问题被约化为常微分方程组的初值问题.这类初值问题是适定的.本文给出了这类初值问题关于时间变量t的幂级数解.
非线性演化方程;初值问题;不变子空间;幂级数解
1 引言

其中ci为任意常数.换言之,称线性子空间Wk为微分算子F的k-维不变子空间,如果F(Wk)⊆Wk.有许多作者都研究了非线性微分算子的不变子空间,并通过对非线性微分算子不变子空间的研究获得非线性演化方程的精确解.Svirshchevskii为了得到非线性微分算子的不变子空间,将其允许的不变子空间视作一个常微分方程的基本解空间[1].Kaptsov通过寻求方程的微分约束,去获得方程中微分算子的不变子空间[2].Galaktioniv研究了带有二次非线性项微分算子的不变子空间,并利用不变子空间构造二次非线性演化方程的广义分离变量解这种构造方法称为不变子空间法[3].Zhdanov利用非经典对称也给出了类似的结果[4].利用这些方法,一个非线性演化方程被约化为一个k-维常微分方程组.
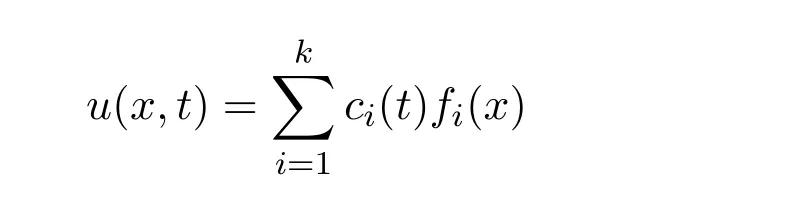
为了研究初值问题(1),首先要将初值问题(1)约化为一个常微分方程组的初值问题.然后,利用这个约化后的初值问题,给出初值问题(1)关于变量t的幂级数解.在第2节中,将讨论这类初值问题的适定性,并证明得到的幂级数解在t=t0的某个邻域内的收敛性.在第3节中,将给出一个例子.
2 初值问题(1)关于时间t的幂级数解
这一节讨论初值问题(1)的适定性,并给出它关于变量t的幂级数解.
假设线性子空间Wk=L{f1(x),···,fk(x)}为微分算子F的k-维不变子空间,即假设(2)式成立,且f(x)∈Wk.此时,f(x)可以表示为

其中ai(i=1,···,k)为某些常数.由不变子空间方法,可以得到初值问题(1)形如

其中i=1,···,k.由此,初值问题(1)被约化为常微分方程组初值问题(4).
由非线性常微分方程组初值问题的解的存在唯一性定理及解的可微性定理知,在初值问题(4)中,如果关于cj(i,j=1,···,k)有一阶连续偏导数,那么初值问题(4)在t=t0的某个邻域内存在唯一的连续解,且这个解作为t,t0,ai的函数,在它的存在范围内是连续可微的[5].由函数F的光滑性以及u(x,t)的表达式(3),易知函数关于cj(i,j=1,···,k)也充分光滑.因此,有下面的定理成立.
定理1初值问题(1)是适定的.
利用初值问题(4)和链式法则,可以给出ci(t)在t=t0处的各阶导数.这些导数可以按照如下公式给出:

并且由Cauchy-Kovalevski定理[6]和定理1知,这个幂级数解在此邻域内是收敛的.另外,由非线性常微分方程组初值问题的解的延拓与连续性定理[5],初值问题(1)的解还可以被连续地延拓.
3 举例

[1]Svirshchevskii S R.Ordinary differential operators possessing invariant subspaces of polynomial type[J]. Comm.Non.Sci.Num.Sim.,2004,9:105-115.
[2]Kaptsov O V,Vererkin I V.Differential constraints and exact solutions of nonlinear diffusion equations[J]. J.Phys.A:Math.Gen.,2003,36:1401-1414.
[3]Galaktionov V A.Invariant subspaces and new exact solutions to evolution equations with quadratic nonlinearities[J].Proc.Royal Soc.Endinburgh,1995,125A:225-246.
[4]Zhdanov R Z,Andreitsev A Y.Non-classical reductions of initial-value problems for a class of nonlinear evolution equations[J].J.Phys.A:Math.Gen.,2000,33:5763-5781.
[5]王高雄,周之铭,朱思铭,等.常微分方程[M].2版.北京:高等教育出版社,2003.
[6]Mcowen R C.偏微分方程-方法及应用(天元基金影印系列丛书)[M].北京:清华大学出版社,2004.
Power series solutions of initial value problems for a class of nonlinear evolution equations
ZHU Chun-rong1,2,WANG Jian-qiang1
(1.College of Mathematics and Computer Science,Anhui Normal University,Wuhu241000,China; 2.Department of Mathematics,Northwest University,Xi’an710069,China)
The initial problems of a class of nonlinear evolution equations were considered in this paper,which can be reduced to the initial problems of a class of systems of ordinary partial differential equations by invariant subspace method.The initial value problems are well posed.The power series solutions with respect to variable t of the initial problems are presented.
nonlinear evolution equations,initial value problem,invariant subspace,power series solutions
O175.29
A
1008-5513(2009)04-0749-03
2008-10-29.
西北大学研究生自主创新资助项目(07YZZ15),安徽师范大学青年基金(2009xqn55).
朱春蓉(1979-),讲师,博士研究生,研究方向:偏微分方程.
2000MSC:35G25,35C10

