m分Cantor尘的H ausdorff测度
曾超益,袁德辉
(韩山师范学院数学与信息技术系,广东潮州 521041)
m分Cantor尘的H ausdorff测度
曾超益,袁德辉
(韩山师范学院数学与信息技术系,广东潮州 521041)
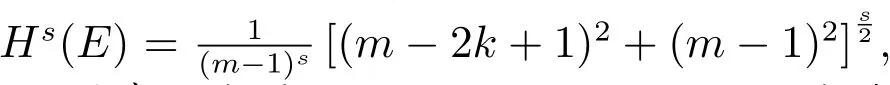
相似分形;m分Cantor尘;Hausdorff测度;p级拷贝
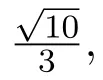
1 m分Cantor尘的构造


2 几个引理
对于相似分形的Hausdorff维数S>1时,目前尚未有好的例子得到它的Hausdorff测度的准确值,文[4-5]分别给出了最佳覆盖,几乎处处覆盖的概念,从理论上说,对于这样的覆盖的寻找也是十分困难,即使对于S≤1的S―集,Hs(E)=|E|s的例子也很少,只有三分Cantor集,4分Cantor尘,4分Sierpinski地毯几个典型的例子.为了求得m分Cantor尘的Hausdorff测度的准确值,我们先给出几个引理.
引理1若平面开集U包含m分Cantor尘的相邻两类上标相同的两个p级拷贝(p= 1,2,…),则

3 主要定理
根据m分Cantor尘的几何结构和Hausdorff测度的定义,我们有:



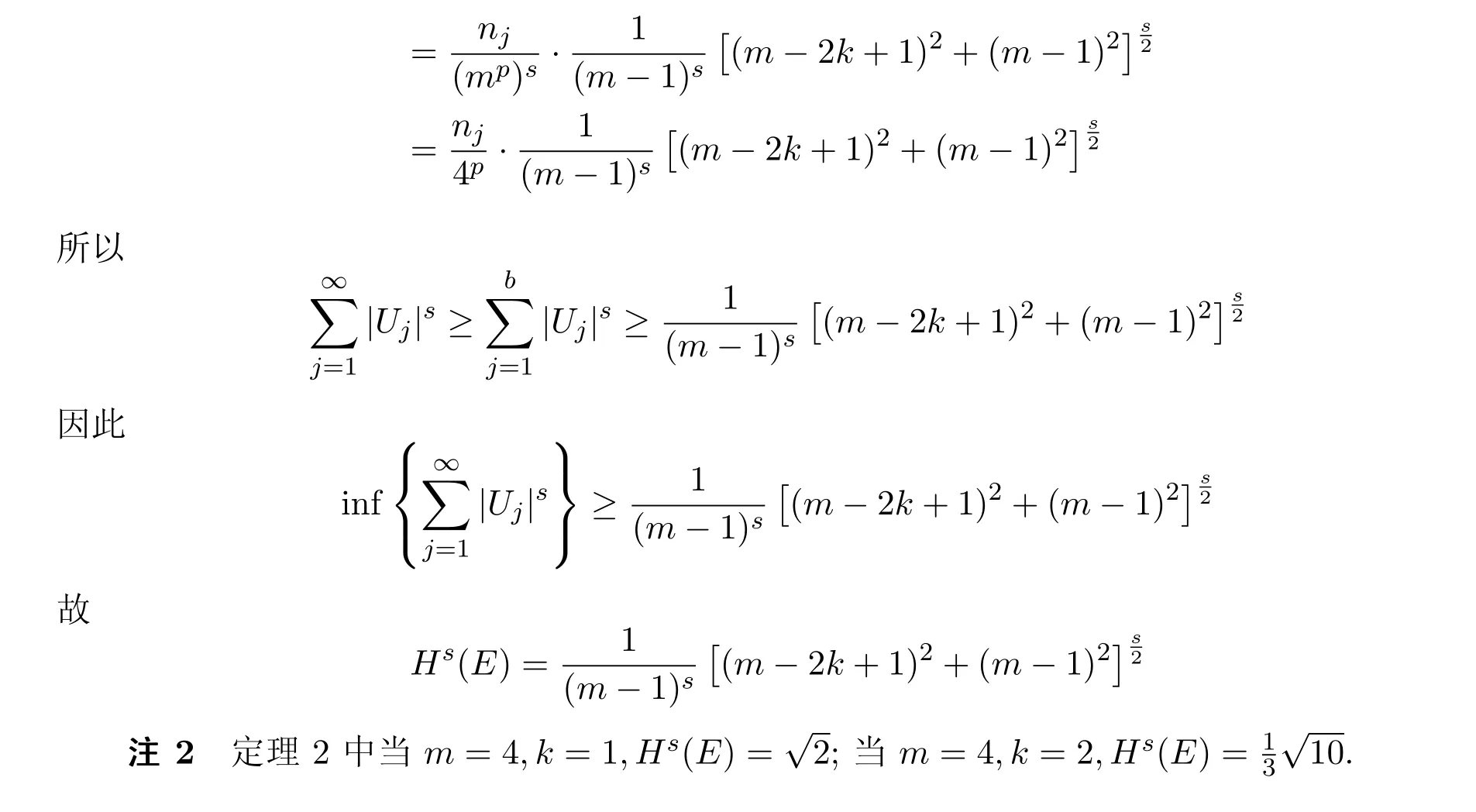
[1]何伟弘,罗俊,贾保国.Cantor尘和Sierpinski地毯[J].中山大学学报:自然科学版,1999,38(4):117-119.
[2]曾超益,许绍元.Cantor尘的Hausdorff测度的初等证明[J].数学的实践与认识,2003,33(6):78-82.
[3]曾超益,许绍元.一个.Sierpinski地毯的Hausdorff测度的初等证明[J].数学的实践与认识,2006,36(2):234-237.
[4]Zhou Z L,Li F.Twelve open problems on the exact value of the Hausdorff m easure and on topological entropy:a brief survey of recent results[J].Institute of Physics Publishing,Non-Linearity.2004,17:493-502.
[5]许绍元,李国祯.关于自相似集存在最好-几乎处处闭集覆盖的充分必要条件[J].江西师范大学学报:自然科学版, 2004,28(3):203-205.
[6]曾超益.m分非均匀Cantor集的Hausdorff测度[J].纯粹数学与应用数学,2006,22(1):120-123,135.
Hausdorffm easure of m-Cantor Dust
ZENG Chao-yi,YUAN De-hui
(Department of Mathematics,Hanshan Normal University,Chaozhou 710071,China)
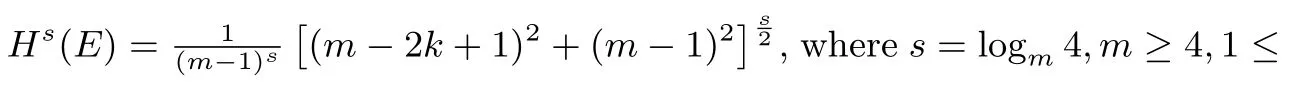
Hausdorffm easure,sim ilar fractal,m-Cantor dust,p-copy
O174.12
A
1008-5513(2009)02-0356-07
2007-11-10.
广东省教育科研课题(JYKY 04039),江西省自然科学基金项目(0611005).
曾超益(1958-),副教授,研究方向:分形几何.
2000M SC:41A 10

