具有Clifford断面的正则纯正半群

孙京锋,邵勇

(西北大学数学系,陕西西安 710127)

具有Clifford断面的正则纯正半群

孙京锋,邵勇

(西北大学数学系,陕西西安 710127)

给出了具有Clifford断面的右正规纯正半群的等价刻画,得到了具有Clifford断面的正则纯正半群的次直积分解,证明了具有Clifford断面的正则纯正半群一定是正则纯正群.

同余；正则纯正半群；Clifford断面；次直积

1 预备知识

设S为半群,a∈S,如果存在x∈S,满足axa=a,则称a为正则的.如果对于任意的a∈S,a都是正则的,则称S为正则半群[1].

定义1[1]称正则半群S为纯正半群,若S的幂等元之集E(S)是S的子半群.

设S为纯正半群,E(S)为S的幂等元之集.若E(S)为左正则带,即对任意的x,y∈E(S) 有xyx=xy,则称S为左逆半群[6].若E(S)为右正则带,即对任意的x,y∈E(S)有xyx= yx,则称S为右逆半群[6].若E(S)为正则带,即对任意的x,y,z∈E(S)有xyxzx=xyzx,则称S为正则纯正半群.

设S为半群.a∈S,如果有aa'a=a和a'aa'=a'成立,则称a'为a的逆元.用V(a)来表示a的逆元的全体.若对于任意的a∈S,|V(a)|=1,则称S为逆半群.

定义2[3]设S为正则半群.S的逆子半群S◦称为S的逆断面,如果S◦含且只含有S的每个元的一个逆元,即对于任意的x∈S,|V(x)∩S◦|=1.

x在逆断面S◦中的唯一逆元记作x◦,并且用x◦◦来表示(x◦)◦.

命题1[4,5]设S是具有逆断面S◦的正则半群,则下列结论成立:

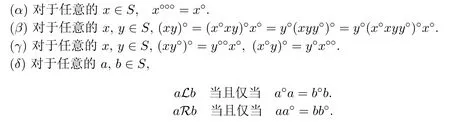
(η)S是纯正的当且仅当对于任意的a,b∈S,(ab)◦=b◦a◦.

(ε)若S是(左,右)正规纯正半群,则对于任意的a,b,c∈S有a◦bc◦=a◦b◦◦c◦.

2 主要结论

设S为具有逆断面S◦的正则半群.若S◦为Clifford半群,即对任意的a∈S◦有a◦a= aa◦,则称S◦为Clifford断面.这样,就有

引理1设S是具有逆断面S◦的纯正半群.若V(x)=V(x◦x2),则S◦为Clifford断面.

证明我们只需证明x◦x◦◦=x◦◦x◦.

对于任意的x∈S有

于是就有x◦◦x◦=x◦x◦◦.故S◦为Clifford断面.

设S是纯正半群,E(S)为S的幂等元之集.若E(S)为右正规带[2],即对任意的e,f,g∈E(S)有ef g=f eg,则称S为右正规纯正半群.若E(S)为左正规带[2],即对任意的e,f,g∈E(S)有ef g=egf,则称S为左正规纯正半群.

设S为半群.称S为完全正则半群[2],是指S的每一个H-类都是S的子群.纯正的完全正则半群称为纯正群[2].设S为纯正群,E(S)为其幂等元之集.若E(S)为右正规带,则称S为右正规纯正群.若E(S)为左正规带,则称S为左正规纯正群.这样,就有下面引理.

引理2若S为具有逆断面S◦的右正规纯正半群,则下列命题等价:

这样,我们得到本节的主要结果.

定理3设S为具有Clifford断面的正则纯正半群,则S为正则纯正群.

证明由定理2知S/σ为左逆半群,且S◦/σ为S/σ的Clifford断面.由推论1知S/σ为左正则纯正群.由推论2知S/η为右逆半群,且S◦/η为S/η逆断面.由定理1知S/η为右正则纯正群.于是,由引理4可得S同构于左正则纯正群S/σ与右正则纯正群S/η的次直积.从而,S为完全正则的.故S为正则纯正群.

[1]How ie JM.Fundam entals of Sem igroup Theory[M].Oxford:Oxford Science Publication,1995.

[2]Petrich M,Reilly NR.Com p letely Regular Sem igroups[M].New York:W iley,1999.

[3]B lyth TS,M cfadden R.Regular sem igroups with a mu ltip licative inverse transversal[J].Proc.Roy.Soc. Edinburgh,1982,92A:253-270.

[4]B lyth TS,A lem ida Santos MH.Congruence associated with inverse transversals[J].Collect.Math.1995, 46:35-48.

[5]Blyth TS,A lem ida Santos MH.Amenable orders associated with inverse transversals[J].Journal of A lgebra, 2001,240:143-164.

[6]M iyuki Yamada.Note on a certain class of orthodox sem igroups.Sem igroup Forum[J],1973,6:180-188.

Onregular orthodox sem igroups with Clifford transversals

SUN Jing-feng,SHAO Yong

(Department of Mathematics,Northwest University,Xi’an 710127,China)

We givean equivalent characterization of right norm alorthodox sem igroup with a Clifford transversal and obtain the decom position of subdirect product of regular orthodox sem igroups with Clifford transversals. We also prove that a regu lar orthodox sem igroup with a Clifford transversal is a regular orthogroup.

congruence,regular orthodox sem igroup,Clifford transversal,subdirect product

O152.7

A

1008-5513(2009)02-0310-05

2008-05-21.

国家自然科学基金(10471112),陕西省教育厅自然科学专项基金(07JK 413).

孙京锋(1982-),硕士,研究方向：半群代数理论.

2000M SC:20M 10,06B10