带p-Laplacian算子三点边值问题拟对称正解的多重性

田元生

(湘南学院数学系,湖南郴州 423000)

带p-Laplacian算子三点边值问题拟对称正解的多重性

田元生

(湘南学院数学系,湖南郴州 423000)

应用Avery-Peterson不动点定理,讨论了一类带p-Laplacian算子三点边值问题在非线性项f依赖于未知函数的一阶导数的情况下拟对称正解的多重性,得到了这类边值问题至少存在三个拟对称正解的充分条件.

p-Laplacian算子;三点边值问题;拟对称正解;锥

1 引言

带p-Laplacian算子微分方程的边值问题,在非牛顿力学,宇宙物理,血浆问题和弹性理论等诸多领域都有广泛的应用.人们对此类边值问题正解的存在性进行了深入的研究,取得很多有意义的成果[14].最近几年,对边值问题的对称正解和拟对称正解的存在性及多重性的关注逐渐增多.文[5]通过建立一个线性算子,利用线性算子的谱理论,研究了一类边值问题的对称正解的存在性和多重性.文[6]给出了拟对称函数的定义,应用五个泛函的不动点定理研究了下面边值问题拟对称正解的存在性.本文应用Avery-Peterson不动点定理,把文[7]中得到拟对称正解的存在性和多重性结论,推广到带p-Lpalcian算子的边值问题(Q)上.

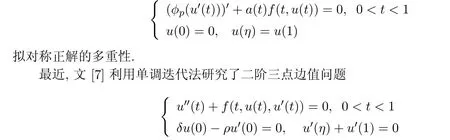
在本文中,总假定以下条件成立

2 预备知识

为了证明本文的主要结果,需要如下的预备知识.

定义2.1设E是一个实Banach空间,如果P是E中某非空凸闭子集,并且满足下面两个条件:

定义2.2设η∈(0,1),称函数u∈C1[0,1]关于η是拟对称的,如果

定义2.3映射α称为P上的非负连续凹泛函,只要α:P−→[0,∞)连续且

对所有的x,y∈P以及0≤t≤1成立.类似地,称映射γ是P上的非负连续凸泛函,只要γ:P−→[0,∞)连续且

对所有的x,y∈P以及0≤t≤1成立.

定义2.4给定正数a,b,c,和d,设γ和θ是P上的非负连续凸泛函,α是P上的非负连续凹函数,ψ是P上的非负连续泛函.定义凸集

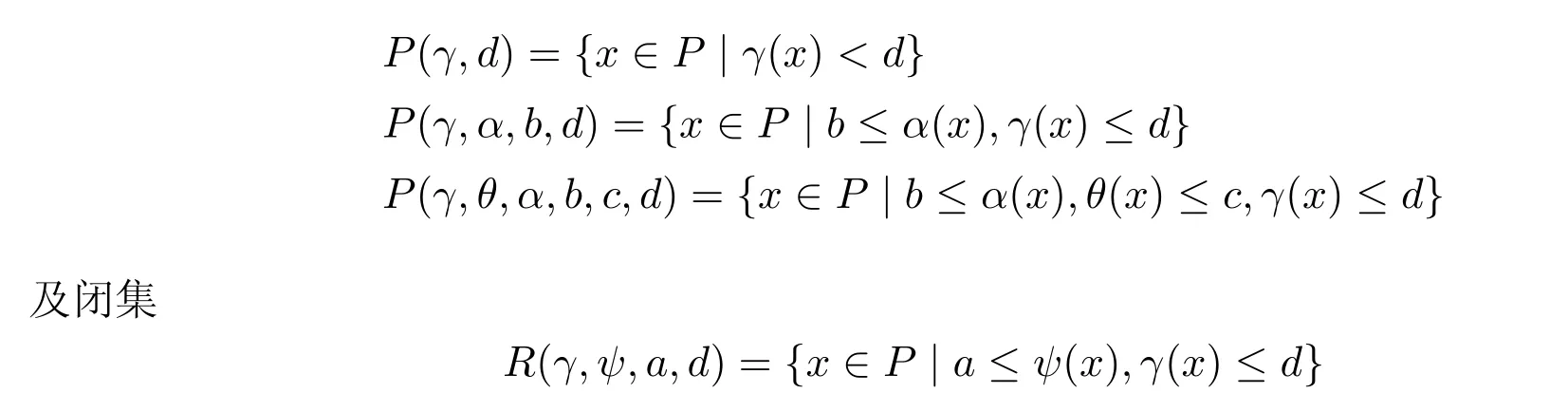
本文主要结论的证明要用下面的Avery-Peterson不动点定理.

定理2.1[8]令P是实Banach空间E中的锥,设γ和θ是P上的非负连续凸泛函,α 是P上的非负连续凹泛函,ψ是P上的非负连续泛函且满足ψ(λx)≤λψ(x),0≤λ≤1,存在正数M和d,使得

3 主要结论及其证明

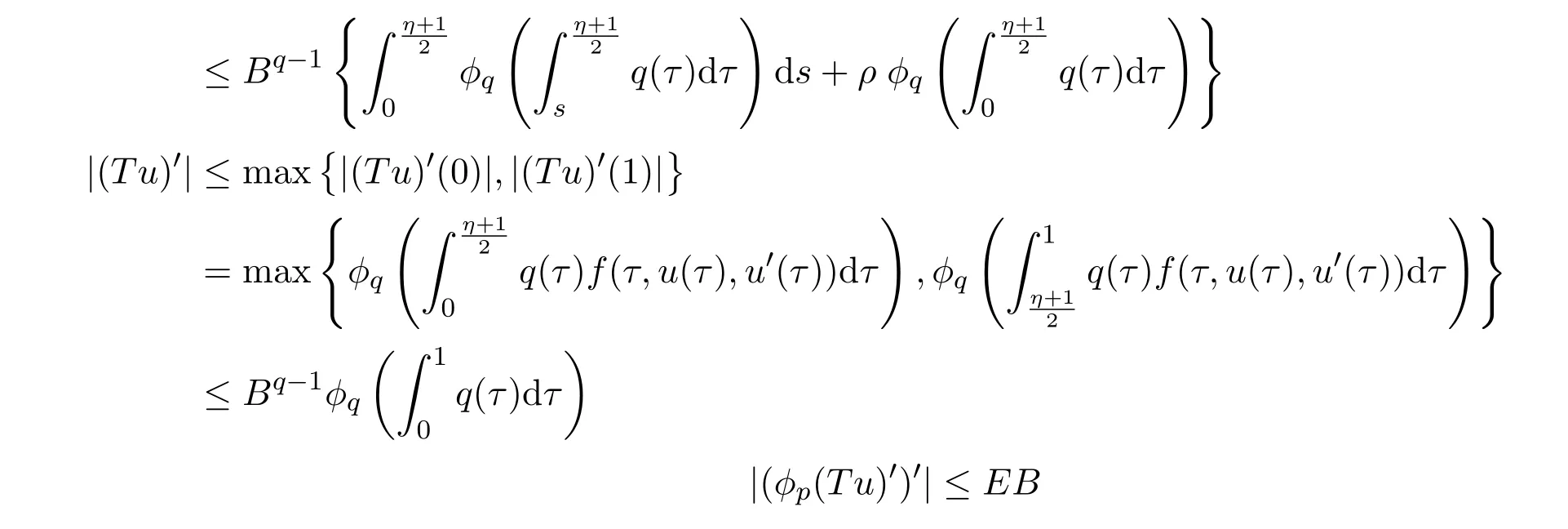
于是,根据A rzela-Ascoli定理知T(D)为列紧集.其次由勒贝格控制收敛定理不难证明T在P上是连续的.因此T:P−→P是全连续的.

为了方便,引用下面记号由条件(A1)知:f(t,u,v)≤φp(d/H).另一方面,对u∈P,有Tu∈P,则Tu在[0,1]上凹,于是

[1]Su H,Wei Z L,Wang B H.The existence of positive solutions for a nonlinear four-point singu lar boundary value prob lem with a p-Laplacian operator[J].Nonlinear Anal.,2007,66:2204-2217.

[2]Jin J X,Y in C H.Positive solutions for the boundary value problems of one-dim ensional p-Laplacian with delay[J].J.Math.Anal.App l.,2007,330:1238-1248.

[3]Sun B,Ge W G,Zhao D X.Three positive solutions for multipoint one-dimensional p-Laplacian boundary value prob lem swith dependence on the first order derivative[J].M ath.Com p.Mode.,2007,45:1170-1178.

[4]M a D X,Han J X,Chen X G.Positive solution of boundary value p roblem for one-dim ensinal p-Laplacian with singu larities[J].J.Math.Anal.App l.,2006,324:118-133.

[5]Sun Y P.Optim alexistence criteria for symm etric positive solutions a three-point boundary value p roblem[J]. Nonlinear Anal.,2007,66:1051-1063.

[6]Avery R I.Henderson J.Existence of three positive pseudo-symm etric solutions for a one-dim ensional p-Laplacian[J].J.M ath.Anal.App l.,2003,277:395-404.

[7]Pang H H,Feng M Q,Ge W G.Existence and m onotone iteration of position solutions for a three-point boundary value problem[J].App l.M ath.Letters,2008,21:656-661.

[8]Avery R I,Peterson A C.Three positive fixed points of nonlinear operators on orderd Banach spaces[J]. Com put.M ath.App l.,2001,42:313-322.

The multip licity of positive pseudo-symm etricsolutions to a three-point boundary value problem of p-Laplacian equations

TIAN Yuan-sheng

(Department of Mathem atics,X iangnan University,Chenzhou,Hunan,423000,China)

By using Avery-Peterson theorem on convex cone,we consider the three-point boundary value problem for p-Lap lace equations with the nonlinear term depending on the first order derivative,the resutlt of three positive pseudo-symm etric solutions are obtained.

p-Laplacian opertor,three-point boundary value porblem,positive pseudo-symm etric solution, cone

O175.8

A

1008-5513(2009)02-0294-08

2008-07-08.

湖南省教育厅科研项目(08C826),湖南省重点建设学科项目,湖南省高校科技创新团队计划项目.

田元生(1962-),副教授,研究方向：微分方程.

2000M SC:34B15