等式约束优化一个新的SQP算法
赵富强,曾玲
(桂林电子科技大学数学与计算科学学院,广西桂林 541004)
等式约束优化一个新的SQP算法
赵富强,曾玲
(桂林电子科技大学数学与计算科学学院,广西桂林 541004)
提出了一个处理等式约束优化问题新的SQP算法,该算法通过求解一个增广Lagrange函数的拟New ton方法推导出一个等式约束二次规划子问题,从而获得下降方向.罚因子具有自动调节性,并能避免趋于无穷.为克服M aratos效应采用增广Lagrange函数作为效益函数并结合二阶步校正方法.在适当的条件下,证明算法是全局收敛的,并且具有超线性收敛速度.
等式约束优化;SQP算法;等式约束二次规划;全局收敛;超线性收敛
1 引言
本文考虑如下优化问题
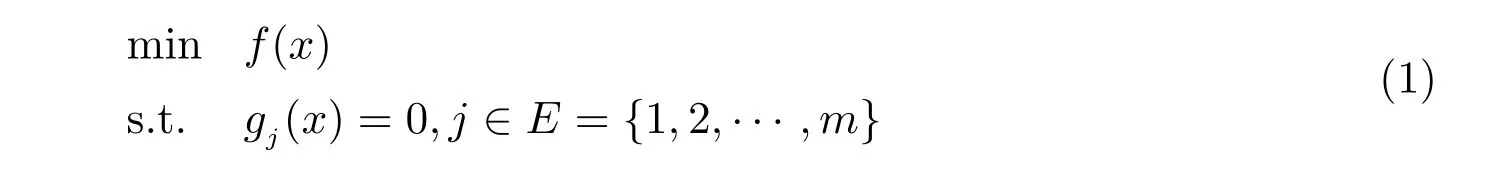
其中f,gj(j∈E)为连续可微函数.求解问题(1)的SQP方法是一个迭代算法。即:每一步迭代中其搜索方向dk是通过求解一个下列形式的二次规划所得
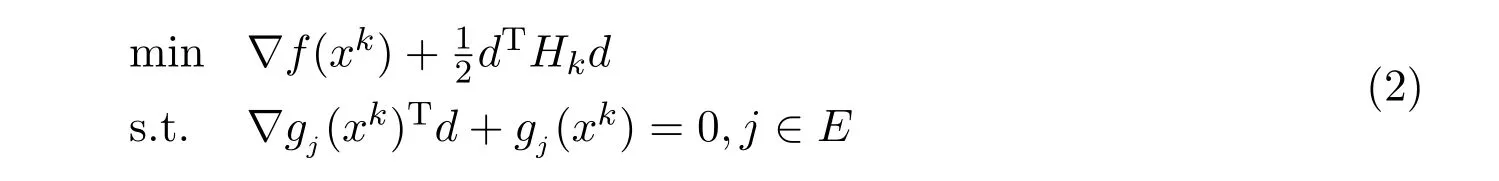
这里Hk是一对称正定矩阵.迭代具有下列形式xk+1=xk+tkdk.其中tk是通过某一效益函数采取一维搜索得到的步长.
序列二次规划(SQP)算法一直是求解非线形约束优化问题的有效方法之一,70年代以来该类算法的研究一直是非线形规划研究领域的一个热点,并出现了大量的研究成果文[1-11].然而SQP方法目前仍面临着一个重要的困难:
(1)SQP算法要求迭代过程中每一个二次规划子问题都有解.由于子问题的约束条件是原问题的线形近似,因此而产生的约束区域可能是空集.
(2)存在Maratos效应.即:即使迭代点非常接近问题(1)的最优点时也不能保证步长为1.
本文对等式约束优化问题进一步研究,我们利用文[1]的思想通过求解增广Lagrange函数极小点的拟New ton法推导出二次规划子问题,这样可以保证每一步迭代都有可行解dk并且是下降方向.同时吸收文[3]中罚因子调整方法,经过分析避免罚因子趋于无穷.为克服M aratos效应,利用增广Lagrange函数作为效益函数,同时结合二阶步校正方法,在适当的条件下,证明了算法的全局收敛性与超线性收敛性.
2 算法及其理论基础



3 算法的全局收敛性

4 算法的超线性收敛性
本节讨论算法的超线性收敛性.首先证明算法产生的点列{xk}整列收敛于x∗.为此,需另作如下假设:

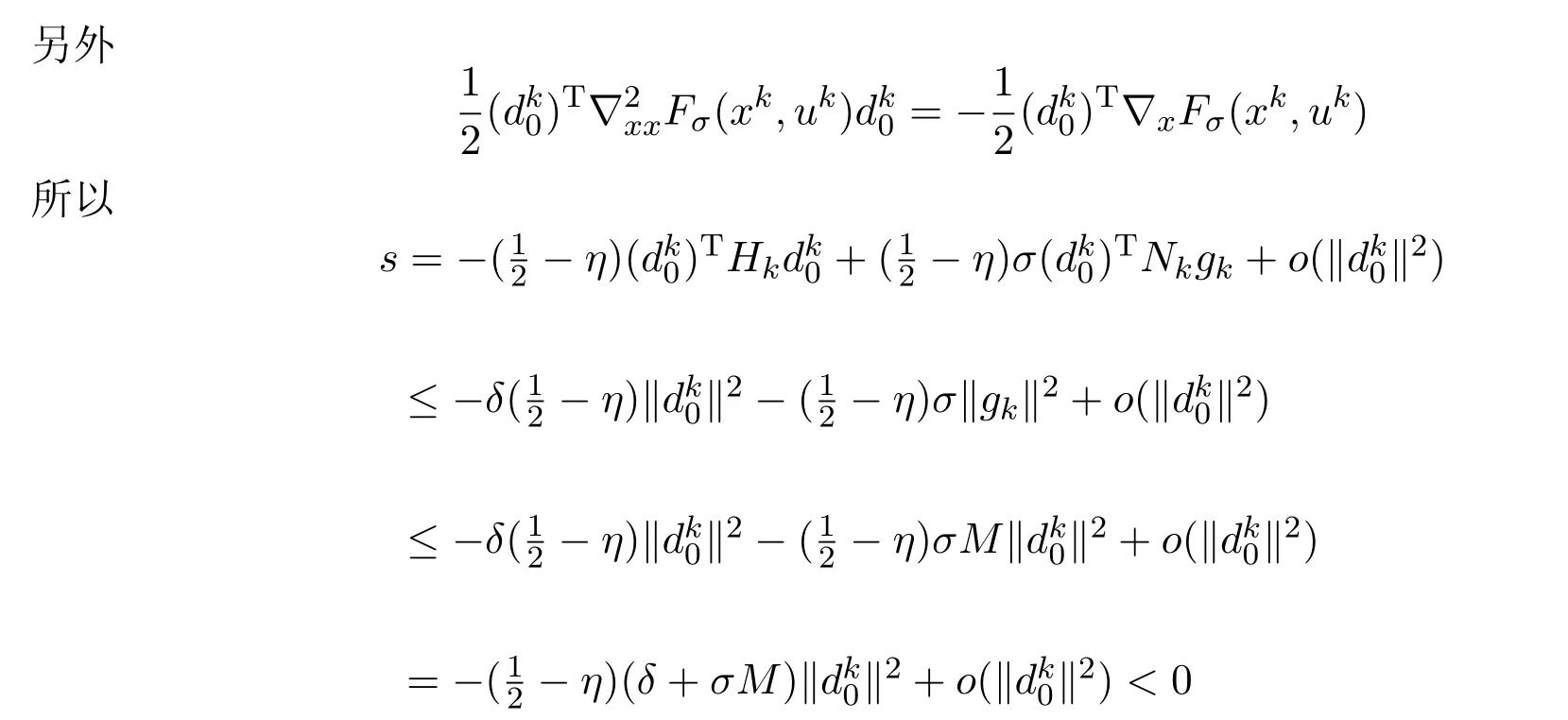
由引理7及文[9]之定理5.2或文[12]之定理12.3.3知有以下收敛性定理成立.
定理2算法是超线性收敛的,即
心理素质包括认知、情感、意志、个性等智力与非智力方面的品质,是人的心理能量的体现。学生的体质水平与心理品质具有一定程度的正相关,他们在力量、运动速度、耐力、反应灵敏性等方面的欠缺,或者跑、跳跃、投掷、攀登、悬垂、支撑等运动能力不强,往往影响他们参与其他活动的心理状态,使他们表现出畏惧困难、竞争意识不强、团队意识差、意志品质薄弱、心理承受能力差等心理弱点。因此,高职院校体育教育必须以科学的方式方法培养和训练学生,使他们具备较强的运动能力、良好的心肺功能、健壮匀称的体格体型,进而以独特的方式培养学生良好的心理品质,帮助学生在成长过程中不断完善自我。
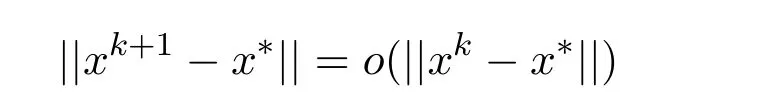
4 数值实验
本节我们用M atlab软件及其工具箱编程,在一定范围内对实际例子进行数值试验.在以下算例中统一参数取值为


表1算法A的数值实验结果
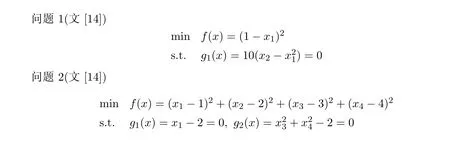
参考文献
[1]王秀国,薛毅.基于增广Lagrange函数的RQP方法[J].计算数学,2003,11:393-406.
[2]张菊亮,章祥荪.一个等式约束问题的SQP方法及其收敛性[J].应用数学学报,2001,24(1):1-9.
[3]朱志斌.一般约束最优化强收敛的拟乘子-强次可行方向法[J].经济数学,2001,18(3):80-87.
[4]聂普炎.等式约束情况下多项式函数的乘子法[J].云南大学学报:自然科学版,2000,22(3):165-168.
[5]高自友,贺国平,赖炎连.具有相容子问题的序列二次规划算法[J].中国科学:A辑,1996,26(11):991-1001.
[6]朱志斌,张可村.不等式约束优化一个新的SQP算法[J].计算数学,2004,4:413-426.
[8]Powell M J D,Yuan Y.A recursive quad ratic programming algorithm that uses differentiable exact penalty function[J].M ath.Programming,1986,35:265-278.
[9]Facchinei F,Lucidi S.Quadraticly and superlinearly convergent for the solution of inequality constrained optim ization p roblem[J].JOTA,1995,85(2):265-289.
[10]Zhu Zhibin,Zhang Kecun,Jian Jinbao.An im proved SQP algorithm for inquality constrained optim iza tion[J].Mathem atical methods of Opertions Research,2003,58:271-282.
[11]Zhou G L.A modified SQP method and its global convergence[J].Jouunal of G lobal optim ization,1997,11: 193-205.
[12]袁亚湘,孙文瑜.最优化理论与算法[M].北京:科学出版社,1997.
[13]王宜举,修乃华.非线形规划理论与算法[M].西安:陕西科学技术出版社,2004.
[14]Hock W,Schittkowski K.Test Exam p les for Nonlinear Programming Codes[M]//Lecture Notes In Econom ics and Mathem atical System s.Berlin:Springer,1987.
A new SQP algorithm for equality constrainedop timization
ZHAofu-qiang,ZENG Ling
(School of Mathematics and computing Science,Guilin University of Electronic and Technology, Guilin 541004,China)
In this paper,a new SQPm ethod is presented to solve equality constrained optim ization.It obtains descent direction by solving a equality constrained op tim ization subprob lem which is deduced by solving the augm ented Lagrangian in quasi-New ton m ethod.The penalty param eter is ad justed autom atically and avoided tending to infinity.In order to conquer M aratos effect,it takes augm ented Lagrangian as a merit function and combines two-step revised method.Under some suitable assum ptions,we p rove that the algorithm is global convergence as well as superlinear convergence.
equality constrained optim ization,SQP algorithm,equality constrained quadratic programming, global convergence,superlinear convergence
O221.2
A
1008-5513(2009)02-0276-08
2008-06-10.
国家自然科学基金(10501009),广西自然科学基金(0728206).
赵富强(1982-),在读硕士.研究方向:最优化理论与方法.
2000M SC:90C30

