不确定时滞模糊系统的时滞相关鲁棒H∞控制*
张 果,李俊民
(西安电子科技大学理学院, 陕西 西安 710071)
非线性是工业控制中普遍存在的现象,基于T-S模型的模糊控制是一种研究非线性系统比较成功的方法[1-8]。不确定性在实际系统中是普遍存在的,其研究有着很强的应用背景[1-2]。时滞现象也常存在于许多实际系统中,其存在会引起系统性能的下降,甚至导致系统的不稳定,因此对模糊时滞系统的研究引起了许多学者的关注[2-6]。其研究结果分为时滞无关和时滞相关[3-6]。通常时滞相关较时滞无关有小的保守性,特别在时滞较小的情况下。对模糊时滞系统进行稳定分析时,常用模型转换方法和边界不等式来估计交叉乘积项的上界[5-6]。为减少保守性,文[6,9]分别引入了自由权值矩阵和模糊自由权值矩阵方法。但上述成果多是基于公共的Lyapunov-Krasovskii泛函(LKF)[2,4]。为了减少公共LKF方法的保守性,文[6]提出了模糊LKF方法研究时滞系统的稳定性,但没有考虑不确定问题和H∞性能。
本文研究了一类带有时变时滞的不确定模糊系统的鲁棒H∞控制问题。定义一个模糊LKF, 并且在推导过程中引入多个包含时滞项的模糊自由权值矩阵。根据并行分布补偿算法(PDC),得到了闭环系统时滞相关的鲁棒渐近稳定条件。
1 系统描述
由T-S模型描述的带有时变时滞的不确定非线性系统,它的第i条规则可描述如下
(1)


通过单点模糊化,乘积推理和中心平均反模糊化方法,模糊系统的总体模型为:
(2)

根据PDC设计控制器,第i个子系统的控制律为:


(3)
thenu(t)=Kix(t)
整个系统的控制律可表示为:
ξ(t))Kix(t)
(4)
把(4)代入(2)中,闭环系统可表示为:

以下给出在证明中要用到的引理:
引理1[10]设M,N和F(t)是维数适合的实矩阵且满足FT(t)F(t)≤I,则对于ε>0有如下不等式成立:MTF(t)N+NTFT(t)M≤εMTM+ε-1NTN。
引理2[8]设A,D,E,F是合适维数的实数矩阵,且FT(t)F(t)≤I,则有矩阵P>0对于标量ε>0满足εI-DTPD>0时,有如下不等式成立
(A+DFE)TP(A+DFE)≤
ATPA+ATPD(εI-DTPD)-1DTPA+εETE
2 主要结果
2.1 稳定性分析
引入带有时滞的模糊自由权值矩阵
(6)
其中Xki,Yk,i∈S,k=1,2,3,4是待定的合适维数的常数矩阵。以下分别记Xi(t)为Xi,i=1,3,4,记X2(t-d)为X2。
定理1 对于给定的常数ρ>0,τ>0和σ>0,如果对于正常数εm,m=1,2,...,5存在正定对称矩阵P,Qi,Ri,Xki和Yk,k=1,2,3,4,i∈S满足矩阵不等式(7)和(8),则系统(5)在H∞性能指标ρ下是鲁棒渐近稳定的。
,i,l,m∈S
(7)

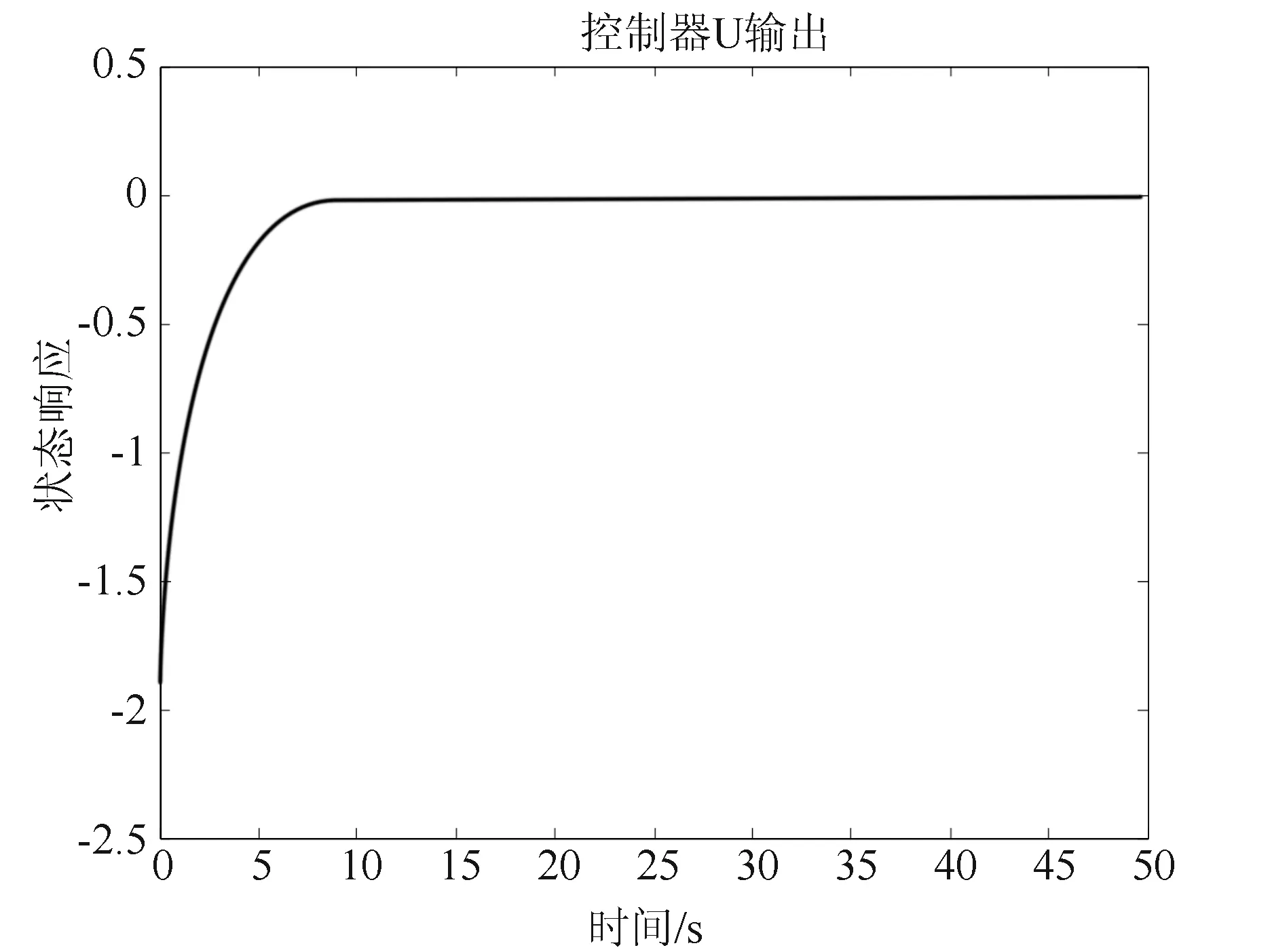
i (8) 其中 φij=(Ci+DiKj)T(Ci+DiKj) +(Ci+DiKj)T 证明选取模糊Lyapunov-Krasovkii泛函: (9) 首先考虑w(t)≡0,时闭环系统的渐近稳定性。当w(t)≡0,闭环系统(5)可表示为: ξ(t))hj(ξ(t))[(Ai+BiKj+ ΔAi)x(t)+(Adi+ΔAadi)xd(t)] (10) 沿着系统(10)的轨线,对V(x(t))求导,由Leibniz-Newton公式,可得到: ≤ξ(t))hl(ξ(t-d))× [(Ai+BiKj+ΔAi)x(t)+(Adi+ΔAadi)xd(t)- (11) 由引理1知 (12) hl(ξ(t-d))hm(ξ(s))ηT(t)×(Φij,l+Φji,l+ (13) 考虑定理1中的(7)-(8)式分别等价于 (14) <0,i (15) 以下考虑零初始条件φ(t)=0,t∈[-τ,0],w(t)≠0时的闭环系统(5)的H∞性能。沿着系统(5)的轨线对V(x(t))求导,并引入公式Leibniz-Newton和系统方程(5),可得: (16) 同样由引理1可得: 由引理2可知(14)式可修正为: hj(ξ(t))xT(t)φijx(t)-ρ2wT(t)w(t) (18) (19) 使用Schur补定理,由定理1可知: (20) 积分后可得: V(t)-V(0)<0 (21) ,i,l,m∈S (22) (23) 其中 λ1(AiZ+BiMj)T λ1(CjZ+DjMi)Tλ1(CiZ+DiMj)TH2i 综上述分析,下面给出控制器设计方法: 证明根据Kj=MjZ-1可知Mj=KjZ,代入(22)和(23)中。由(22)-(23)和(24)-(25)的等价性可知系统(5)在H∞性能指标ρ下是鲁棒渐近稳定的。 考虑如下一个带有时滞的不确定模糊系统: Ri: ifx1∈M1 x(t-d)+Biu(t)+Bwiw(t) z(t)=(Ci+ΔCi)x(t)+Diu(t) ,i=1,2 其中, Bw1=Bw2=-0.5;C1=C2=[-0.6 0] D1=D2=0.1;Ec1=Ec2=[-0.1 0] H21=H22=0.3 图1 系统状态响应曲线 本文研究了一类带有时变时滞的连续不确定模糊系统的时滞相关鲁棒H∞控制问题。在推导过程中,没有采用模型转换和边界不等式,而是引入了多个包含时滞项的模糊自由权值矩阵。基于模糊LKF和并行分布补偿算法,得到了闭环系统时滞相关鲁棒稳定新的条件,且控制器可以通过一组LMIs的解求得。最后由算例验证了该方法的有效性。 图2 控制曲线 参考文献: [1] IKEDA T, WANG H O. Robust stabilization of a class of uncertain nonlinear systems via fuzzy control: Quadratic stability H-infinity control theory and linear matrix inequalities [J]. IEEE Trans on Fuzzy Systems, 1996, 4(1): 1-13. [2] YONEYAMA J. Robust stability and stabilization for uncertain Takagi-Sugeno fuzzy time-delay systems [J]. Fuzzy Sets and Systems, 2007, 158:115-134. [3] ZHOU S, LI T. Robust stabilization for delayed discrete-time fuzzy systems via basis-dependent Lyapunov-Krasovskii function [J]. Fuzzy Sets and Systems, 2005, 151:139-153. [4] CHEN B, LIU X P. Fuzzy guaranteed cost control for nonlinear systems with time-varying delay [J]. IEEE Trans on Fuzzy Systems, 2005, 13(2): 238-249. [5] GUAN X P, CHEN C L. Delay-dependent guaranteed cost control or T-S fuzzy systems with time delays [J]. IEEE Trans on Fuzzy Systems, 2004, 12(2): 236-249. [6] WU H N, LI H X. New approach to delay-dependent stability analysis and stabilization for continuous-time fuzzy systems with time-varying delay [J]. IEEE Trans on Fuzzy Systems, 2007, 15 (3): 482-493. [7] TANAKA K, HORI T, WANG H. A multiple Lyapunov function approach to stabilization of fuzzy control systems [J]. IEEE Trans on Fuzzy Systems, 2003, 11(4):582-589. [8] YI Z, HENG P A. Stability of fuzzy control systems with bounded uncertain delays [J]. IEEE Trans on Fuzzy Systems, 2002, 10 (1):92-97. [9] HE Y, WU M, SHE J H, et al. Parameter-dependent Lyapunov functional for stability of time-delay systems with polytopic-type uncertainties [J]. IEEE Trans on Automatic Control, 2004, 49 (5):828-832. [10] LI X, SOUZA C E DE. Delayed-dependent robust stability and stabilization of uncertain linear delay systems: a linear matrix inequality approach [J]. IEEE Trans on Automatic Control, 1997, 42(8):1144-1148.







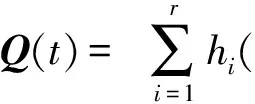














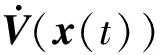
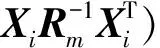







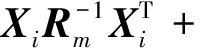


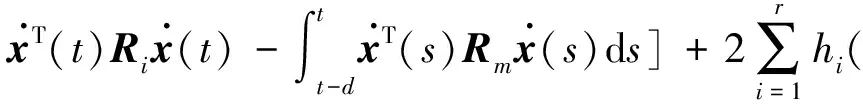


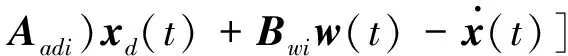
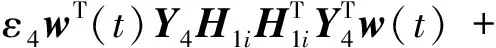
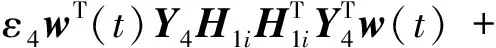
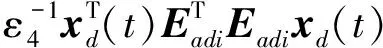

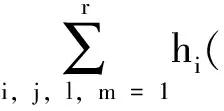






2.2 控制器的设计
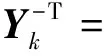





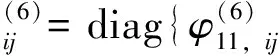


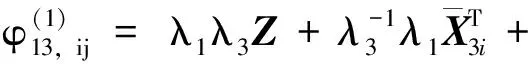




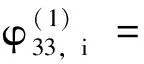












3 数例分析


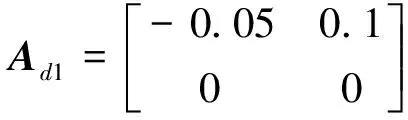
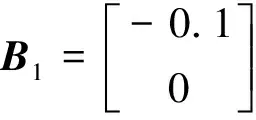


4 结 论