一道习题的启示
罗 平
教学圆的周长后,我给学生安排了教材上的一些练习,另外增加了一道题(如下图):一只圆柱形油桶的底面半径是0.2米,与墙相距31.6米。如果把油桶滚到墙边,至少要滚几圈?

没想到全班学生48人,仅有5人做对,正确率为10.4%。大部分学生认为滚动的路程就是31.6米,即31.6÷(2×3.14×0.2)=31.6÷1.256≈25(圈)。
这不由得引起了我的思考:怎样的练习是学生发展所必需的?怎样设计和组织课堂练习,才能保证课堂教学的有效?
随后,我增加了一节练习课,安排了如下练习题:
1.把一只圆柱形油桶从东墙边挪到西墙边,已知东、西墙之间的距离是63.2米,油桶的底面半径是0.2米。如果把油桶滚过去,至少要滚几圈?
我让学生亲自滚一滚,通过操作,大部分学生都能理解,油桶滚动的距离应是油桶开始时底面圆心到靠近西墙面时底面圆心之间的距离。这个油桶应滚动(63.2-0.2×2)÷(2×3.14×0.2)=62.8÷1.256=50(圈)。
2.一个边长为10厘米的正方形内有一个半径为2厘米的小圆,这个圆在正方形内沿正方形的周长滚动一周,滚动的路程是多少厘米?
3.将两个1元硬币正面朝上平放在桌上,使两个“1”头对头地位于同一条直线上(如图1),将左边一个按住不动,右边一个紧贴左边硬币滚动一周。仔细观察:右边这个滚动的硬币本身转了几圈?
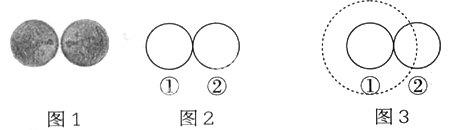
我们将两个硬币用两个圆来代替(如图2),即圆①固定,圆②绕圆①转一圈。许多学生认为圆②经过的路程就是它圆周上的点绕圆①的长度,即圆①的周长,所以圆②自身转动一圈。通过实验可以发现圆②转了两圈。事实上,圆②真正经过的路程并不是圆①的周长,而是它的圆心绕圆①经过的路程(如图3中的虚线图)。因此,假设圆的直径为d,则虚线圆的直径为2d,所以圆②自身转动2圈。通过操作,学生较好地理解完成了本题。
4.如果两个圆的半径之比是1∶2,那么小圆绕大圆一周自身转了几圈?
反思:
课堂练习是小学数学课堂教学的重要组成部分,是学生学习过程中不可缺少的重要环节,是学生掌握知识、形成技能、发展智力的重要手段和必要途径,同时也是教师获得反馈信息的有效载体。因此,数学课堂有效的练习设计是有效教学管理理念下教师应该共同思考的问题。那么,如何进行有效的练习设计呢?
1.设计的课堂练习应该与生活贴近。
小学数学内容,大多可以联系学生的生活实际。因此,在设计练习时,应多考虑从实际问题出发,设计富有情趣和意义的活动,使学生切实体验到数学就在自己身边,从而激发他们进一步学习的积极情感,学以致用,并在应用中加深理解,实现数学的应用价值。
2.设计的课堂练习应该有利于培养学生的思维能力。
教师要挖掘教材中的潜在价值,创造性地将其拓展,通过具体的、有趣的、富有挑战性的数学习题去激发学生的思维,提高习题的含金量。
练习设计要有坡度,为学生提供思维及想象的阶梯。可先设计一些模仿性的练习,然后逐步提高要求,并适时增加一些富有变化和发展性的练习,防止产生思维定势。
3.设计的课堂练习应该注重实践性。
数学教学应遵循学生的认知规律,强调从学生已有的生活经验出发,让学生亲身经历将实际问题抽象成数学模型并进行解释与应用的过程。动手操作符合儿童生理发展的特点,对于小学生学习数学知识、掌握数学原理具有重要作用。为此,倡导数学练习设计的实践性,让学生在体验中学习知识,在实践中理解和运用知识。

