从探究中的逻辑问题谈起
张新春
《中小学数学》小学版2008年第11期发表了浙江上虞陆建江老师《探究到底要多深》一文,文中陆老师在听完“三角形内角和”一课并与专家现场对话后,作了自己的思考。主要涉及对以下教学环节的认识。
师:(拿出一张长方形纸)老师把这个长方形沿对角线剪成两个直角三角形,你能想办法再来验证三角形内角和是180度吗?
在学生思考较长时间后,教师引导两位学生完成以下推导(完成方式1的推导后,教师问“怎样拼成锐角三角形来验证?”):
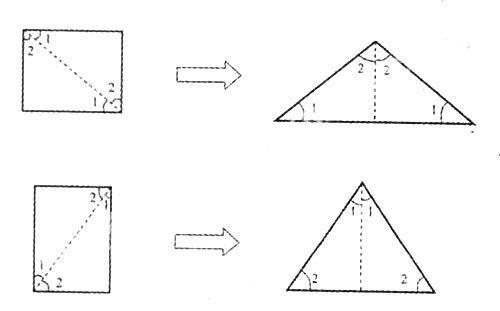
具体验证方法是,通过观察图形,得到三角形内角和即为(∠1+∠2)×2=90°×2=180°
陆老师质疑的是探究需不需要这样深。笔者在此要说的是,不管探究深浅,首先是不能有逻辑上的大问题。
探究三角形内角和的逻辑是:任意给定一个三角形,它的内角和是定值吗?如果是,这个定值是多少(当然,在这里,这两个问题是同时解决的)?而教师引导学生做的事是:将一个长方形剪成两个三角形,将这两个三角形拼成一个新的三角形,这个三角形的内角和是180度。显然这是两个不同的的问题。首先,因为一个长方形剪成两个三角形,用这两个三角形拼成的三角形都是等腰三角形,教师通过这一系列的研究,充其量引导学生探究了等腰三角形的内角和是180度,对于一般的三角形根本没有涉及。
另一方面,即使是要探究一个等腰三角形内角和是180度,符合逻辑的做法也不能是这位老师这样的做法,而应按完全相反的做法施行。即先任意给定一个等腰三角形,再沿这个等腰三角形底边上的高剪开,得到两个直角三角形,这两个直角三角形拼在一起是一个长方形。

也许有读者会说,在小学,用得着讲这么多逻辑吗?你再讲逻辑,三角形内角和还不是通过几个特例后即作出一般结论!逻辑的力量同样很弱。笔者要说的是,科学性与量力性相结合的原则无疑要坚持,但这个原则指的是,如果对科学性的要求超出学生的认识水平,量学生之力而不能接受,则按此原则适当牺牲科学性要求,以达到学生能理解的目的。如三角形内角和问题,若硬是要从平行公理开始,则与学生的认识水平不相适应,学生无法接受,因此,我们采用实验的方法,不完全归纳的方法得到结论。但即使是实验,即使是不完全归纳,我们也应该尽可能使其逻辑性稍强,比如举例时不限于某一种特殊情况,而是尽可能各种类型的例都举出来验证一番。强调这种意义上的逻辑性完全在学生的认识水平范围之内。让学生在其能力与认识水平范围之内思考问题尽量符合逻辑,考虑问题尽量全面,这也应该是数学教学的基本意义所在。
以上为其一。
其二,陆老师文章中介绍的专家评课时指出,四边形的内角和是由三角形内角和推导出来的,由长方形的内角和推出三角形的内角和有循环论证之嫌。由此看来,评课的专家也看重逻辑问题。但到底应该如何看待用长方形内角和推导三角形内角和的问题呢?笔者认为,这里不存在循环论证的问题,因为长方形的内角和并不需要由三角形内角和定理得到。所谓四边形内角和由三角形内角和推导,指的是一般的四边形。像平行四边形(特殊的如长方形)、梯形这类特殊的四边形,其内角和是不必由三角形内角和定理推出,而只需利用其定义并得用平行线的有关公理、定理即可得到。
那么,如何利用长方形的内角和(准确的说是利用长方形四个角都是直角)的结论来推得三角形内角和是180度才是合符逻辑的呢?
首先,对于任意直角三角形,其内角和是180度。这一点由两个完全一样的直角三角形可以拼成一个长方形即可得到(值得注意的是,这里是用任意给定的、即要研究的直角三角形拼出长方形,而不是用长方形来剪出直角三角形。换句话说,对于任意给定的直角三角形,都可以找到一个长方形,沿对角线剪开后,得到的三角形与给定的三角形是完全一样的,总之,出发点必须是任意给定的三角形,而不是长方形)。

其次,对于任意三角形,总可以通过作某一条高,将其分成两个直角三角形。这两个直角三角形的内角和之和是360度,这个和与原来三角形的内角和相比,多出一个平角,于是原来三角形的内角和是180度。
值得说明的是,三角形是最基本的多边形,直角三角形是特殊的三角形,研究多边形的内角和,从三角形开始,继而从直角三角形开始,这种从简单到复杂,从特殊到一般的思路是研究问题很自然的思路。笔者曾用完全类似于上述方法处理过多边形面积的教学,效果较好。其基本思路是在长方形面积计算方法的基础上,得到直角三角形的面积计算,继而任意一个三角形,都可以通过作高分成两上直角三角形,这两上直角三角形面积之和即为原三角形面积(钝角三角形处理起来有点特殊,有一种情况是两个直角三角形面积之差)。于是平行四边形,梯形面积都只需通过对角线将其分割成两个三角形处理即可。这里同样充满从特殊到一般,从未知到已知的转化。
(责任编辑:李再湘)

