基于进化规划算法的舰船辐射噪声分类

丁永忠 方 兴

1海军驻西安东风仪表厂军事代表室，陕西 西安710065 2海军驻第七O九研究所军事代表室，湖北 武汉430070

基于进化规划算法的舰船辐射噪声分类

丁永忠1方 兴2

1海军驻西安东风仪表厂军事代表室，陕西 西安710065 2海军驻第七O九研究所军事代表室，湖北 武汉430070

神经网络分类器在舰船辐射噪声分类中得到了广泛的应用。针对神经网络分类器的设计困难，提出一种基于进化规划算法的设计方法。在该方法中，进化算法的适应度函数不是取为神经网络分类器对训练样本的识别率，而是对训练样本的可分性和聚合度同时考虑，这样能够在保证识别精度的前提下，使网络分类器具有良好的泛化能力，而且该方法不仅能够对待识别的样本进行离线学习，也能够在线学习。使用该分类器对舰船辐射噪声进行分类识别试验，结果表明该方法设计的分类器具有良好的性能。

神经网络；进化算法；分类器；舰船辐射噪声

1 引言

误差反传（BP）神经网络分类器是最早应用于舰船辐射噪声被动声呐目标的神经网络分类器［1－5］，已经证明，具有合适的隐层结构和隐层节点数目的BP网络能够实现对特征空间任意的（超）曲面划分，但是BP网络的隐层结构以及隐层节点数目的确定是非常困难的，通常需要多次试验方能得到合适的隐层结构和隐层节点数目，而且BP网络对新的样板进行学习时，需要改变所有的网络权值，因此BP网络对新样本的学习速度相当慢，而且BP网络的学习和训练算法一般使用梯度下降法，一旦网络的误差曲面为一个不规则的曲面，BP网络很容易陷入局部最小从而导致识别率的下降。近年来，由于结构简单、学习与训练速度快等原因，径向基函数（RBF）神经网络在模式识别，包括在水声信号分类识别中得到了应用［6－8］。

应用于水声目标识别的RBF网络的隐层训练方法通常均为自组织学习方法［9］，即K－均值聚类算法，在无教师监督的条件下进行。该方法对训练样本在特征空间的分布有较高的要求，并要求给出正确的隐节点数和合适的初始权值。但在实际水声目标识别应用时，这些条件很难同时满足。

在被动声呐目标识别中，异类目标间可能会表现出较多的相似特征，而有些同类目标的特征则可能分布较为离散，使训练样本在特征空间的分布很不均匀。这时，像K－均值聚类算法这样无监督地对训练样本的简单空间分割也就容易产生异类目标间的模糊，从而影响网络的分类性能。另外，对于特征结构复杂的水声目标辐射噪声信号，究竟将特征空间划分成多少个区域 （即取多少个隐节点数），以及每个区域的初始中心取什么值才能较好地将不同模式的特征区分开是很难预先确定的。隐节点数取得太少则必然使不同模式的输入样本归入同一节点代表的区域，造成模式划分的模糊。太多的隐节点则一方面随网络规模的扩大增加了计算复杂度，另一方面也给输出层训练时获得全局极小误差带来了困难。不合适的初始权值则可能会引导网络训练向不正确的区域偏移。因此在本文中，使用双群进化规划算法［10］来解决径向基函数神经网络的隐层结构确定，隐层节点参数（包括中心向量、径向基函数宽度），以及径向基函数神经网络分类器的在线学习及结构调整问题。在本文中把使用进化规划算法设计得到的径向基函数神经网络简称为EPRBF（Evolutionary programming based radial basis function）神经网络。

2 基于双群进化规划算法的RBF隐层设计

设待识别的样本集为X＝｛xi｜i＝1，2，…，N｝，式中xi为一K维模式向量，分类问题就是要找到一个空间模式划分C＝｛C1，C2，…，Cm｝，并满足：

并且使总的类内离散度和

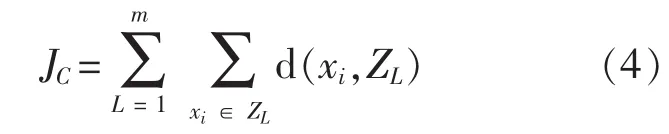
最小。同时借鉴基于支持向量机的模式识别方法［11］，定义类间离散度和：

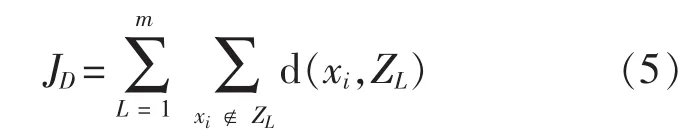
在识别中并使其最大。式中，ZL为第L个聚类的聚类中心，d（xi，ZL）为某一样本到其对应的聚类中心的距离，在本文中使用欧氏距离。则聚类准则函数JC即为各样本到其对应的聚类中心的距离总和；JC最小表征的是具有相似特征的船舶尽量能够聚合为一类；聚类准则函数JD为各样本到其他聚类中心的距离的总和。JD尽量大则表征不同类别的船舶能够尽量的相互区分。

使用进化规划算法求解特定问题的关键在于：

1）如何选择合适的适应度函数来准确地描述需要解决的问题；

2）如何选择合适的个体，将问题的解编码到个体。

显然，对于任意一个分类识别问题而言，同时满足JC最小和JD最大是不可能的，因此必须在类间聚合度和类间可分性间折中。对JC和JD同时进行优化，是进化规划算法中一个很重要的研究方向，即二元优化问题。对于此类二元优化问题，经常使用偏好信息进行决策［12］，使用偏好信息的决策策略是建立在 “决策者愿意承担由于使用自己的偏好进行决策产生的一定风险”的假设基础之上的，由于偏好是决策者的主观的选择趋向，因此对于同一问题不同的决策者很可能产生不同的决策（选择）。为了避免对于同样问题产生不同决策的弊病，在本文中使用一种固定的折中方式来代替决策者的偏好信息。因此定义：

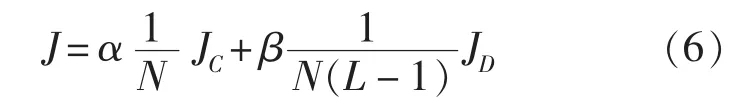
将一个二元优化问题转化为一个一元优化问题。式中，N为样本数目；L为聚类中心数目；α与β为常数。它们不同的取值将影响神经网络分类器的识别精度和推广能力，在本文中α＝β＝0.5。指标J代表一个全局最小值，很多局部极值的函数。因此定义适应度函数：

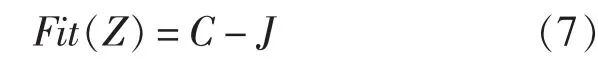
在上式中，C为一个正的大常数，以保证适应度函数的非负性。

在选择了合适的适应度函数以表征问题以后，需要寻找合适的编码机制将问题的解编码到个体。在对J进行优化的过程中，需要求解的参数有两个，一个是聚类中心的数目，另一个是对应于聚类中心数目的聚类中心位置。一般对于神经网络分类器训练而言，训练集中的个体究竟为多少类是已知的，虽然这个已知的数据并不一定正确和准确，但也大概可以表征个体的类别数目。如果把聚类中心数目也作为一个进化规划算法求解的对象，算法将变得极为复杂，需要的计算量也非常大，计算时间很长，同时种群中个体的数目急剧膨胀，需要的存储开销也急剧增加。因此本文并不把聚类中心数目作为进化规划算法的求解对象，而是在已知的分类数目附近分别计算不同的分类数对应的Fit（Z），然后找出其中最大的Fit（Z）所对应的聚类中心数目和聚类中心位置。

本文中使用分阶段的编码方式，首先使用分散编码，经过固定代数的进化找到近似的聚类中心位置，然后使用集中编码方式来求解精确的聚类中心位置。使用进化规划算法对径向基函数神经网络的隐层进行设计的流程如下所述：

1）L＝L0－H1，L为聚类中心数目；L0为训练集已知的大概的分类数；H1为一设定值，与搜索的聚类中心数目的下限有关。

2）判断。如果L＞L0＋H2，比较对应于不同的L的适应度函数Fit（Z），找到最大的Fit（Z）对应的L，以及对应于此个L的聚类中心位置Z1，Z2，…，ZL，输出计算结果。如果L≤L0＋H2，转步骤3）。H2为一设定值，与搜索的聚类中心数目的上限有关。

3）选择合适的种群个体数目N，并有N＝P× L，P为正的常数。种群规模N不能选得很小，如果N很小，在有限次的进化代数内的精度很可能达不到要求。如果N很大，需要的计算时间和计算量以及存储空间要增大很多。因此必须合适地选择种群规模N，在计算速度和计算精度间采取某种折中。选择合适的随机竞争个体数目q，在本文中，令q＝1.5×N，在保证解的精度的前提下，尽量提高算法收敛速度。设置分散编码搜索的最大进化代数Kmax＝500，设置当前进化代数K＝0，选取高斯变异算子标准差的初值σ0＝0.01×个体每一维区间的宽度；

4）种群初始化。对种群的初始化有两种方法，第一种方法是在舰船噪声特征空间中随机产生N个个体作为初始种群，第二种方法是在样本中按照类别随机地选出N个个体作为初始种群。第一种方法虽然更符合进化规划算法种群初始化的一般原则，但是这种方法是在一个空间中从随机的点出发去寻找合适的解，此方法并没有利用训练样本已经有大致的分类结果这一有用的信息，而且其需要的进化代数和进化时间都是很长的，因此本文中并未使用此种方法。在使用第二种初始化方法时有以下几种情况需要考虑：

（a）L＜L0。在此种情况下，在L0个粗略分类中随机选择L个聚类，并在这L个聚类中分别选取出10个个体共10×L个个体作为初始种群。在此种情况下，由于每个聚类包含的个体数目不同，有的聚类中的个体数目可能不足10个。假设此聚类包含Q个个体，首先将这Q个个体全部选出，然后在这Q个个体中随机选择出10-Q个个体，然后与其他子群的个体一起构成初始种群。

（b）L≥L0。在这种情况下，预期的样本聚类数目已经大于已知的粗略的分类数目，因此如何选择那些多出来的聚类中心的初值是问题的关键。首先计算在分类数为L－1时，训练样本集中每一个个体到其对应的聚类中心的欧氏距离，然后选择出其中欧氏距离最大的一个个体作为第L个聚类中心的初值。在此种情况下，依然会有聚类包含的个体数目不足10个的情况，其处理与L＜L0的时候完全相同。

在初始化以后，使用随机编码的方式，对每一个子群中的个体从1～10编码，并称种群中所有编码为1的个体为第一组，其他组则依次类推。

5）判断是否已经到达了最大进化代数，如果已经到达则输出具有最高适应度的组作为集中编码方式进化种群的初始种群，转步骤8），如果没有到达最大进化代数，转步骤6）；

6）所有子群中编码在1～5范围内的个体组成更小的子群组ZS，其他的个体组成子群组ZL，子群组ZS中的个体使用细调高斯变异算子进行变异，并称变异后的子群组为ZS′，子群组ZL中的个体使用粗调高斯变异算子进行变异，并称变异后的子群组为ZL′，对于变异后的子群组中个个体编码采用＋10的方式，即原来编码为X的个体变异产生的后代个体的编码为10＋X；

7）计算每一个子群组的适应度函数，并实用随机q竞争法则，选择出具有最好适应度的10个子群组作为下一代种群，同时对下一代的子群进行编码。根据随机q竞争法则排序的结果，排在第一位的子群组编码为1，并依次类推直至所有的子群组获得编码。K＝K＋1，转步骤5）；

8）将分散编码方式转化为集中编码方式，选择合适的种群个体数目N，合适的随机竞争个体数目q，设置集中编码搜索的最大进化代数Kmax，设置当前进化代数K＝0，选取高斯变异算子标准差的初值σ0＝0.01×个体每一维区间的宽度，设置进化终止条件；

9）采用复制的方式生成N个完全相同的个体作为集中编码进化方式的初始种群，以随机的方式选择N／2个个体作为子群ZS，其他个体组成子群ZL；

10）判断是否已经到达了最大进化代数或者满足了进化终止条件，如果已经到达则输出具有最高适应度的个体作为针对此分类数目的进化计算的结果，转步骤13），如果没有到达最大进化代数，转步骤11）；

11）子群ZS中的个体使用细调高斯变异算子进行变异，并称变异后的子群为ZS′，子群ZL中的个体使用粗调高斯变异算子进行变异，并称变异后的子群为ZL′；

12）计算每一个个体的适应度函数，并实用随机q竞争法则，选择出具有最好适应度的N个子群组作为下一代种群，同时根据随机q竞争法则排序的结果，选择排在前N／2位的个体组成子群ZS，其余个体组成子群ZL。K＝K＋1，转步骤10）；

13）L＝L＋1，转步骤2）。

在确定了隐层节点数目及隐节点中心位置以后，还需要确定的参数就只有径向基的宽度这一个参数。径向基的宽度的确定方法与基于进化规划算法的径向基函数神经网络隐节点中心位置的确定方法基本相似，唯一的不同点就是适应度函数的选择，因此在本文中不再赘述。

3 径向基函数神经网络分类器的在线学习

训练样本总是不完备的，而且，作为一个可以实用的分类识别系统而言，在其使用过程中，随着时间的推移，总要有一些新的舰船加入到待识别的队伍，因此神经网络分类器必须具有在线学习能力，即能够将那些未曾训练过的样本进行准确的分类。

假设在神经网络分类器的使用过程中，遇到一个不属于任何一个已知类别的样本，那么以这个新的样本作为一个聚类中心，并使用进化规划算法对网络的隐层结构进行重新设计和优化，其设计方法与上节的训练方法中增加一个新的类别的训练方法完全一致，因此不再重复。

由于训练样本的不完备性会造成模式空间的划分不尽合理，神经网络会把属于某类目标的样本误判为代表新模式的样本，并被进化规划聚为一个新类，在隐层输出。因此，在神经网络的在线学习过程中，需要合并代表同一目标模式的冗余节点。如果对于同一个输入样本Xi有：

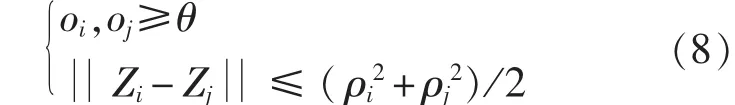
则将第i和第j个隐层节点合并为一个节点。在上式中，oi，oj为第i个和第j个隐节点的输出，Zi，Zj为第i个和第j个隐节点的中心向量，ρi，ρj为第i个和第j个隐节点基函数的宽度。θ是一个设定值，一般取e－1～1之间，θ太小容易造成类间混淆，影响神经网络的识别精度，θ太大容易造成分类过细，造成神经网络的规模急剧膨胀，在本文中，θ取0.72。Zi＝［Zi1，Zi2，…，Zin］为第i个隐层节点的中心向量，那么合并后的新节点为：

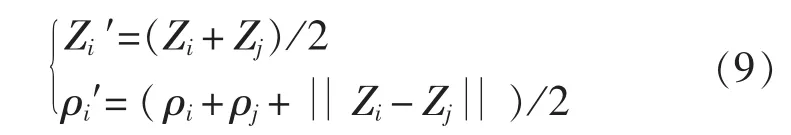
4 舰船辐射噪声分类实验

为检验EPRBF分类器的性能，我们对收集到的44个水面和水下运动目标以及不同海况下的海洋环境噪声的实录信号进行识别试验。其中水面和水下运动目标共有89个不同工况和航次，海洋环境噪声为3种不同海况。所获得的水面、水下运动目标及海洋环境噪声以22 050 Hz采样频率采集信号，取1.486 08 s时间长度的信号，即32 768个数据点构成一个样本，共采集了4 745个数据样本，以此作为试验样本集。在4 745个样本集中选择1 132个样本作为训练集，其余的3 613个样本作为测试集。其中训练集中包含了所有类型的舰船（鱼雷、环境噪声），但是并不包含每类舰船的所有工况（海况）。同时，用A类表示水面舰船，B类表示水下低速运动目标，C类表示水下高速运动目标，D类表示环境噪声。

为了比较EPRBF网络分类器的性能，同样构筑了标准的BP网络分类器和RBF网络分类器作为比照对象。这三种神经网络分类器具有类似的结构，均为三层结构，一个输入层，一个输出层和一个隐层。输出层有4个节点，与A、B、C、D类型相适应，输出层的决策采用赢者独活（Winner Takes All）策略。BP网络和RBF网络的隐层节点数目则根据设定的误差不同而不同，EPRBF网络分类器的隐层结构则是使用进化规划算法优化得到，与误差并没有直接的关系。神经网络的训练均使用成批训练的方法，即每输入100组数据，对网络的权值进行一次调整。各种神经网络在不同的误差下的隐层节点数目、训练时间和识别一个样本所需时间如表1所示。

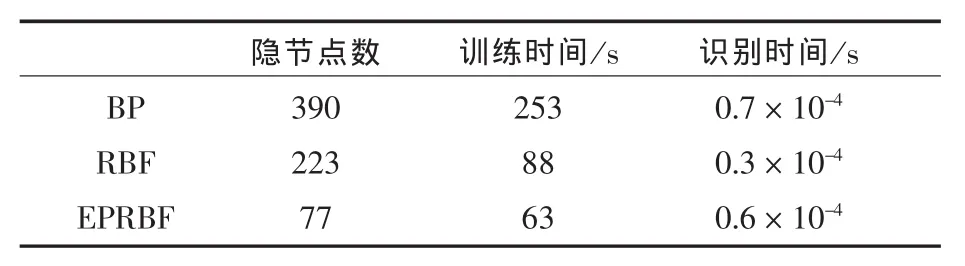
表1 不同网络需要的隐层节点数目、训练时间和识别时间比较

由表1可以看出，在同样的精度要求下，BP网络的结构是最复杂的，需要的隐层节点的数目非常多，网络训练和识别所需要的时间也很长。EPRBF网络的结构最简单，隐层节点数目最少，训练需要的时间也最少，但识别一个样本需要的时间则介于RBF网络和BP之间。

使用不同的神经网络分类器对各类舰船辐射噪声进行分类，神经网络的输入均为基于Dopplerlet变换的舰船辐射噪声特征矢量，不同神经网络分类器的分类识别结果如表2所示。

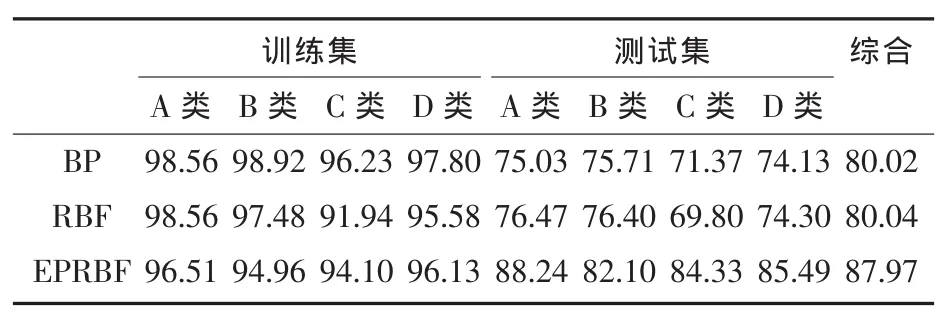
表2 不同神经网络分类器的识别结果（%）

由表2可以看出，EPRBF神经网络分类器对训练集的分类效果比不上BP网络分类器和RBF网络分类器，但是对测试集的分类效果要明显好于其他的网络，而且总体的识别效果有较大的提高。将训练集和测试集的次序打乱，重新选择训练集和测试集对神经网络的识别效果进行测试，依然得到类似表2的结论。

由于训练样本的不完备性，对于一种实用的、可以长期工作的神经网络分类器而言，在其工作期间必然遇见一些训练中未曾学习过的样本，因此神经网络分类器必须具有在线学习能力。显然在海上调动实船做神经网络分类器的在线学习试验是效果最好和最有说服力的，但也是非常难以实现的，因此，本文中通过下述方法来模拟神经网络分类器接收到一个未曾训练过的类型船舶噪声的识别过程。

1）重新选择训练集，在原有的1 132个训练样本集中剔除掉四种类型舰船和一种海况下的海洋环境噪声，四种类型舰船中三种为A类目标，一种为C类目标（18个样本），其中A类目标分别为某型驱逐舰（30个样本）、某型护卫舰（25个样本）和某型导弹快艇（27个样本），因此新组成的训练集共包含1 032个样本；

2）重新构筑网络，并使用重新选择后的训练样本集对BP网络分类器、RBF网络分类器和EPRBF网络分类器重新进行训练；

3）重新选择测试集，新的测试集包含三部分样本，一部分是从原有的训练集中剔除出来的网络分类器未曾学习过类型舰船的特征矢量样本，共计100个。另外一部分是从原有的测试集中挑选出来的网络分类器未曾学习过类型舰船的特征矢量样本，共计413个。最后一部分则是从原有的测试集中挑选出来的网络分类器曾经学习过类型舰船的特征矢量样本1 337个，因此，新组成的测试集共包含1 840个样本；

4）确定测试样本的输入顺序，在本文中使用这样的次序来对网络在线学习能力进行测试。首先输入一些网络学习过的样本，然后输入一些网络未曾学习过的样本，再输入网络学习过的样本，这样交替进行；

5）测试。

三种网络对于未曾学习过的样本识别能力（即在线学习能力）的比较如表3所示。

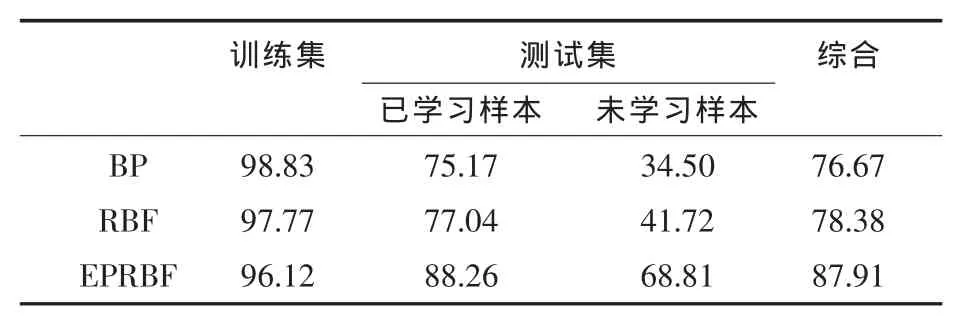
表3 不同神经网络在线学习能力（%）

从表3可以看出，对于一个未曾学习过的舰船类型，EPRBF网络能够很快地掌握它的特征，并记忆在隐层节点中，在以后的识别中加以利用，显然其他两种网络几乎不具有在线的学习能力，对于未曾训练过的样本，识别能力都比较差。

5 结论

神经网络分类器在舰船辐射噪声分类中得到了广泛的应用。针对神经网络分类器的设计困难，本文提出了一种基于进化规划算法的设计方法。使用该方法对RBF神经网络分类器的结构进行了设计，使用设计后得到的RBF神经网络分类器分别进行了离线测试和在线测试。测试结构表明使用该方法设计的神经网络分类器不仅具有良好的离线识别能力，而且均有良好的在线识别能力。

［1］BARAN R H，COUGHLINJ P.A neural network for passive acoustic discrimination between surface and submarine target［J］.Proceeding of SPIE，1991,1471（164）：323－332.

［2］SHEPPARD C P，GENT C R.A neural network based sonar classification system［C］／／Undersea Defence Technology Conference and Exhibition，1992：628－633.

［3］RUSSO A.Constrained feedforward neural network ensembles for recognition of sonar signals using shape［C］／／Undersea Defence Technology Conference and Exhibition，1992：622－627.

［4］GORMAN R P，SEJNOWSKI T J.Learned classification of sonar target using a massively parallel network［J］.IEEE Transc.ASSP，1988，36（7）：1135-1140.

［5］张艳宁，焦李成，靳云姬，等.一种基于自适应高斯神经网络的船舶噪声分类方法［J］.声学学报，1998，23（4）：349－356.

［6］方世良，陆佶人.复合基函数神经网络在水声目标识别中的应用［J］.声学技术，1998，17（2）：54－62.

［7］方世良.一种应用于水声目标识别的隐层结构自适应网络［J］.东南大学学报，1999，29（3）：89－94.

［8］方世良.一个聚类数动态可调的水声信号聚类算法［J］. 1996，21（4）：525－530.

［9］GROSSBERG S.Compectitive learning：from interactive activation to adaptive resonance［J］.Cognitive Science，1987，11（1）：23－63.

［10］王向军，向东，蒋涛，等.一种双群进化规划算法［J］.计算机学报，2006，29（5）：835－839.

［11］DERICHE M，TEWFIK A H.Maximum likelihood estimation of the parameters of discrete fractionally differenced Gaussian noise process［J］.IEEE Trans.On Signal Processing，1993，41（10）：2977－2989.

［12］KALPLAN L M，KUO C C J.Fractal estimation from noisy data via discrete fractional Gaussian noise（DFGN）and the Harr basis［J］.IEEE Trans.On Signal Processing，1993，41（2）：3554－3562.

Classification of Ship Radiation Noise Using Evolutionary Algorithm

Ding Yong－zhong1Fang Xing2
1 Naval Representative Office at No.872 Manufactory，Xian 710065，China 2 Naval Representative Office at No.709 Research Institude，Wuhan 430070，China

Neural network classifier is widely used in ship radiation noise classification.According to the design difficulty of neural network classifier，an approach using evolutionary programming is proposed in the paper.Fitness function of evolutionary algorithm is not the classification rate of neural network but the combination of decentralization and conglomeration，then both the training set classification rate and testing set classification rate of neural network are high.Using this method，the neural network can learn online and offline.Ship radiation noise identification experiment using this neural network is done，and experiment results show that the neural network classifier using evolutionary programming has good performance.

neural network；evolutionary algorithm；classifier；warship radiation noise

U666；TP18

A

1673－3185（2009）04－47－05

2009-05-07

丁永忠（1970－），男，工程师，硕士。研究方向：鱼雷制导与控制。E-mail：dingyongzhong@qq.com

方 兴（1974-），男，工程师，硕士。研究方向：数字信息处理