舰船舱室内部爆炸的数值模拟研究
孔祥韶 吴卫国 李晓彬 徐双喜 黄 涛
1武汉理工大学 交通学院,湖北 武汉430063 2高速船舶工程教育部重点实验室,湖北 武汉430063
舰船舱室内部爆炸的数值模拟研究
孔祥韶1,2吴卫国1,2李晓彬1徐双喜1黄 涛1
1武汉理工大学 交通学院,湖北 武汉430063 2高速船舶工程教育部重点实验室,湖北 武汉430063
反舰武器战斗部在舰船舷侧防护结构内部爆炸将造成舱室的严重破坏,数值模拟是分析结构在爆炸载荷作用下破坏情况的有效手段之一。舱室内部爆炸的数值模拟涉及到冲击波传播、多个流场与结构的耦合、结构的变形与破坏。文章基于MSC.Dytran软件平台,实现了舱室内部爆炸的数值模拟。研究表明,在舱壁开口有利于减小舱室角隅处的汇集压力,保护舱室结构。同时,爆炸产生的二次破片对舱室结构能产生进一步毁伤效果。
舱室结构;多欧拉域耦合;冲击波;二次破片
1 引言
随着反舰武器的日益发展,舰船在作战中极有可能受到精确制导武器攻击。高能量爆炸冲击波和目标结构的复杂耦合问题已引起研究人员的重视。近年来,国内外学者针对爆炸载荷作用下结构的响应问题开展了大量的试验和数值仿真研究。刘土光[1]等对固支加筋方板在爆炸载荷作用下的刚塑性动力响应进行了理论和试验研究,提出了最大残余变形的理论计算公式;吴有生[2]等应用能量方法推导了爆炸载荷下舰船板架的塑性变形和破损的计算公式;朱锡[3]等通过试验研究了船体板架在水下接触爆炸作用下的破口,分析了加强筋对破口长度的影响,提出了板架结构加强筋的相对刚度;杜志鹏、李晓彬[4]等应用Dytran模拟舰船舷侧防护结构在内部爆炸作用下的破坏情况,分析了冲击波在舱室内的传播规律;王世来[5]采用Dytran中的一般耦合计算方法对大型水面舰船舷侧多层防护结构水舱和空舱内爆炸流场及其对舱壁结构造成的变形与破损进行了数值模拟分析。彭兴宁、聂武[6]等利用能量法推导了在爆炸载荷作用下防护舱壁塑性薄膜大变形的计算公式,并对防护舱壁的设计要求进行了讨论。Ramajeyathilagam[7]应用DYNA3D研究了矩形板的变形与开裂问题,并与试验结果进行了比较。现代舰船舷侧都设置了防护结构,但由于保密的原因,这方面的文献很少。关于泻爆孔对舱室角隅处压力汇聚影响的研究没有见到相关文献,有必要对舱室内爆的细节问题进行深入的研究。
本文应用MSC.Dytran软件,采用多欧拉域流固一般快速耦合算法,模拟了舰船舷侧结构空舱部分爆炸冲击波作用下的变形和破坏情况,研究舱壁开孔(泻爆孔)对冲击波压力在舱室角隅汇集和舱室破坏的影响,并通过接触算法模拟分析了由爆炸产生的二次破片对舱壁的破坏情况。
2 有限元模型
大型水面舰艇舷侧防护结构舱室布置示意图如图1所示。本文研究防护结构第一层空舱(膨胀舱)在爆炸作用下舱壁的局部破坏情况,取A、B、C 3个舱室作为研究对象,不考虑舱室加筋的影响。结构的有限元模型如图2所示。3个舱室的尺寸均为2 m×2 m×2 m,板厚为10 mm,其中A舱室和B舱室之间有直径为0.5 m的开孔 (泻爆孔),模拟爆炸发生在B舱室的中部。结构全部采用Lagrange板单元进行模拟,共划分8 166个节点,8 320个单元。
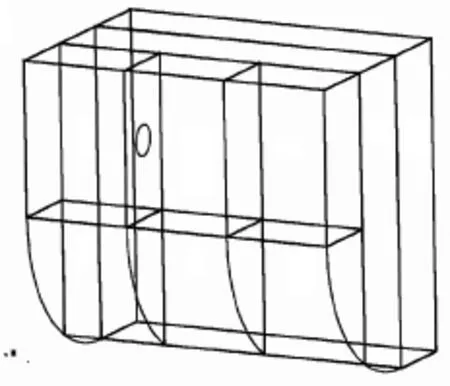
图1 舰船舷侧防护结构示意图
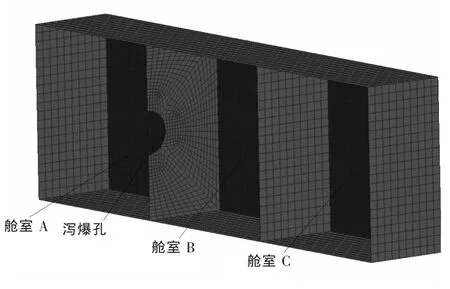
图2 舱室结构有限元模型
每个舱室内部及外部的空气全部采用三维Euler体单元,通过MSC·dytran里的mesh卡片进行网格划分,共产生134 999个单元。
网格划分后空气的有限元模型如图3所示。

图3 4个欧拉域(空气)有限元模型
2.1 舱室结构材料参数
舱室结构用Lagrange四边形板单元模拟,采用三点高斯积分。板的本构关系采用Dytran中各向同性、具有破坏模式的弹塑性材料来定义(DMATEP),采用各向同性强化双线性应力-应变屈服模式和von-Mises屈服准则。屈服应力σ0=350×106Pa,强化模量为Eh=2.5×109Pa。静态屈服应力σsy由下式得到:
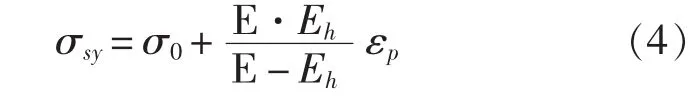
式中,杨氏模量E=2.0×1011Pa;εp为等效塑性应变。材料的破坏准则定义为最大等效应变,当等效塑性应变超过0.15时发生破坏。
材料在高速冲击下其应力应变关系与静态情况下有很大的区别。考虑应变率影响而通常适用的本构方程是Cowper-Symonds方程,由以下超应力法则描述:
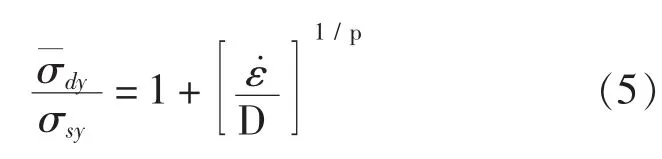
式中,ε˙为等效塑性应变率;σ¯dy是动态屈服应力;σsy为静态屈服应力。式中常数D和p是不同材料的适宜系数,可通过试验得到。对于低碳钢,D=40 s-1,p=4.74。
2.2 空气材料参数及状态方程
舱室内外部的空气全部采用三维Euler体单元模拟,划分为4个欧拉域,分别为A、B、C舱室内部的空气域和舱室外部整体空气域。舱室外部的域以舱室表面为边界,材料存在于舱室外表面,舱室内表面没有材料存在。舱室内部包括的部分由内部域模拟,该域被舱室表面封闭。内部域的材料在舱室内表面而外表面没有材料。因此两个欧拉域的流场边界均为舱室表面。在爆轰冲击波传播的过程中,舱室结构可能发生破坏,内部的空气流到外部,即耦合面发生破坏。
气体所采用的Gamma律状态方程如下式:

式中,p,ρ,e分别表示气体的压力、密度和比内能;γ为气体的比热。在计算中ρ=1.2 kg/m3,e=2.1×105J/kg,气体的初始压力为大气压。
本文将炸药模拟为高压气体球,气体球的半径为0.75 m,密度为25 kg/m3,设定欧拉初始条件时通过设置高压气体球的优先级来定义爆炸。
2.3 流体与固体的耦合方法
在Dytran程序中,Lagrange求解器和Euler求解器是分开的,需要定义二者之间的耦合关系,否则即使Lagrange单元和Euler单元节点相连也不会对Euler材料的流动产生影响,Lagrange单元自身也不会受到Euler单元压力的作用。程序中有任意拉格朗日欧拉(ALE)和一般耦合(General Coupling)两种耦合方法。当用ALE方法定义耦合时,需要在耦合处各个节点相联,使建模繁琐,此外不能使用高精度的黎曼(Roe)求解器。一般耦合方法,其优点在于可使用程序中的卡片进行Euler网格划分和耦合定义,不需要耦合面上各个节点相连接,简化了建模工作,同时可采用高精度的Roe求解器。但其要求结构是封闭的,如遇不封闭的情况,则必须建立哑元(dummy element)进行封闭,同时欧拉单元必须包围拉格朗日单元[8],舱室之间耦合示意图如图4所示。

图4 多欧拉域耦合示意图
本文中对于舱室结构与空气的耦合,采用一般耦合方法。对于舱壁上的开孔采用dummy element单元模拟,保证耦合面封闭。当结构遭受爆炸产生的冲击波作用时发生破坏失效,冲击波通过破口和舱壁开口流入相邻舱室。为了模拟这个物理过程,在Dytran中使用COUP1FL定义耦合面失效。当耦合面的一部分失效时相应的单元就被删除,自动产生一个新的多孔面,随之爆炸气体可以从耦合面上流过。
2.4 边界条件
将结构两端固定作为边界条件,气体除耦合面外全部采用自由流动的边界条件。
3 计算结果分析
模拟为爆炸物的高压气体球位于舱室B正中部,半径为0.75 m,用Dytran计算,计算时间为0.02 s。高压气体以冲击波的形式快速向外传播,在到达舱室结构时与其发生相互作用,造成舱室结构的变形和破坏。图5(a)、(b)显示了冲击波的传播和与结构相互作用的情况。

图5 冲击波传播及与结构相互作用
3.1 泻爆孔对冲击波压力角隅汇集的影响
在冲击波的传播过程中,舱室角隅位置会出现冲击波汇集情况[9],即角隅位置的压力因汇集反射冲击波而增大。从计算结果提取出如图6所示D、E点的压力值,对比泻爆孔对冲击波压力角隅汇集的影响。
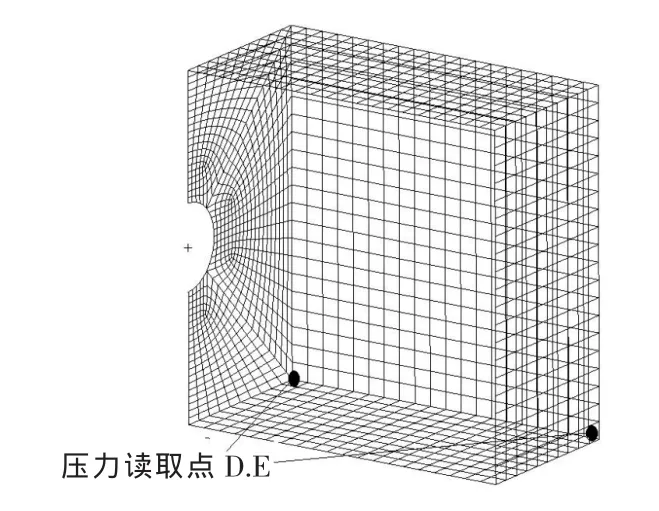
图6 舱室B中压力值读取点示意图
D和E点的压力时程曲线如图7所示,计算时间为0.000 6 s时冲击波压力达到最大值。未开泻爆孔一侧舱室的角隅压力达到1.5×108Pa,泻爆孔一侧的角隅压力为6.23×107Pa。E点的压力值为D点的2倍以上,是由于冲击波通过泻爆孔流入A舱室,从而减小了B舱室的角隅汇集压力。这将直接影响舱室的破坏模式。

图7 舱室B角隅D、E点压力值
3.2 舱室结构的破坏
舱室结构在冲击波压力作用下发生变形和破坏,不同时刻舱室的响应见图8~图10。图8为0.001 8 s时舱室结构的破坏情况,舱室B和舱室C的连接处发生较大的变形并出现破口,因为该位置冲击波压力较大,最大值达到1.5×108Pa。有泻爆孔的舱壁没有发生破坏,但在冲击波作用下发生局部破坏并形成破片,如图9所示。舱室B破坏严重,如图10所示。没有开孔的舱壁与主体结构之间产生很大的破口,而开孔的舱壁只是出现了局部破坏,并没有在舱壁连接处发生破坏,保持了结构的完整性。

图8 舱室结构的变形和破坏

图9 有泻爆孔的舱壁的破坏情况

图10 B舱室的破坏
3.3 爆炸产生的二次破片对舱壁的作用
如图11所示,在计算进行到0.002 8 s时有泻爆孔的舱壁发生破损并产生破片。这些破片在冲击波压力作用下加速运动,最后与舱壁碰撞。如果破片的运动能量足够大,将具有一定的穿甲能力,对舱壁造成破坏以至于损失其水密性。
本文采用接触算法模拟爆炸产生的二次破片对A舱室壁的作用,接触面分别为开有泻爆孔的舱壁和破片可能作用的目标面。因为破片的扩散具有一定的随机性,所以其作用的目标面为A舱室中除开孔舱壁外的其他5个壁面。在Dytran程序中,首先通过程序中的参数设置定义接触,PARAM,CONTACT,THICK,0.0,板壳单元厚度因子取为0。在程序计算过程中具体定义的接触定义如下:
CONTACT,100,ELEM,ELEM,333,444,,,,+
+,V4,BOTH,,YES;
自适应从属面定义:
SET1,333,1,THRU,1400;
自适应主面定义:
SET1,444,3121,THRU,3520,1521,THRU,1920,2321,++,THRU,2720,1921,THRU,2320,2721,THRU,3120
如图11(a)、(b)所示,通过对比发现,未定义接触时爆炸产生的二次破片穿过途经的舱壁面飞出,这与实际情况不符。定义接触时产生的破片在到达目标面时与之发生碰撞而使其运动受到限制,破片的速度约为236 m/s,与舱壁发生碰撞,使碰撞区域发生变形,破片出现回弹现象并没有出现穿透舱壁面的情况。
爆炸产生的二次破片的分布具有随机性,其动能大小也不能确定,对舱壁的破坏作用需要从方法和理论上进行更深入的分析研究。另外,从计算时间而言,对于同样规模的问题进行计算时,采用接触算法所需要的时间大约4倍于不使用接触算法的情况(4CPU、8G内存并行计算时,二者所需的时间分别为40 h和11 h),计算成本(时间)大幅上升,对于这种模拟方法也需要进行进一步探讨。
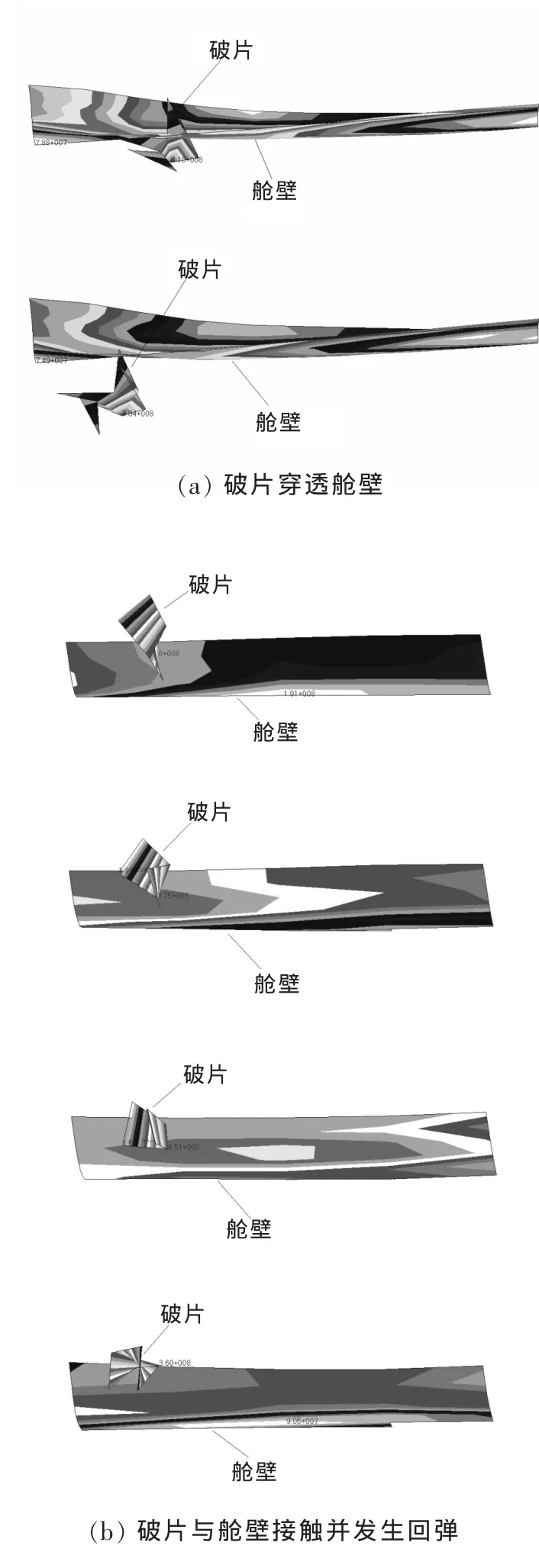
图11 爆炸产生的二次破片对舱壁的作用
4 结束语
通过数值模拟舰船典型防护结构空舱部分在内爆作用下冲击波的传播和结构的响应,分析开有泻爆孔的舱壁在爆炸载荷下的破坏过程,得到以下结论:
1)分析对比B舱室横舱壁有泻爆孔和无泻爆孔两侧角隅压力,发现舱壁开孔(泻爆孔)可以有效降低冲击波压力在角隅处的汇集。未开孔一侧舱室连接处被撕裂破坏,出现大尺寸破口,开孔一侧舱壁出现局部破坏,而舱室连接处没有出现破坏情况,结构保持完整。
2)由爆炸产生的二次破片(开孔舱壁局部破坏而产生的破片),可对有初始应力的舱室结构造成二次毁伤。毁伤效果与爆炸当量、冲击波压力和随机破片尺寸密切相关,需要进一步深入研究。
[1]刘土光,胡要武,郑际嘉.固支方板在爆炸载荷作用下的刚塑性动力响应分析[J].爆炸与冲击,1994,14(1):55-65.
[2]吴有生,彭兴宁,赵本立.爆炸载荷作用下舰船板架的变形与破损[J].中国造船,1995(4):55-61.
[3]朱锡,白雪飞,黄若波,等.船体板架在水下接触爆炸作用下的破口试验[J].中国造船,2003(44):47-52.
[4]DU Zhipeng,LI Xiaobin,et al.Numerical simulation of warship broadside protective structure rupture under inner explosion[J].Journal of Ship Mechanics,2007,11(3):453-461.
[5]王世来.大型水面舰船防护水舱内爆炸的数值模拟[J].浙江工业大学学报,2007,35(3):262-266.
[6]彭兴宁,聂武,等.爆炸载荷作用下舰船防护舱壁的薄膜效应研究[J].船舶力学,2007,11(5):744-751.
[7]Ramajeyathilagam.Deforamation and rupture of thin rectangular plates subjected to underwater shock[J].Int.J.Impact Eng,2004,30:699-719.
[8]MSC.Dytran Theory Manual(Version 2005)[M].MSC Software Corporation,2005.
[9]侯海量,朱锡,梅志远.舱内爆炸载荷及舱室板架结构的失效模式分析.爆炸与冲击,2007,27(2):152-158.
Numerical Simulation of Cabin Structure Under Inner Explosion
Kong Xiang-shao1,2Wu Wei-guo1,2Li Xiao-bin1Xu Shuang-xi1Huang Tao1
1 School of Transportation,Wuhan University of Technology,Wuhan 430063,China 2 Key Laboratory of High Speed Ship Engineering,Ministry of Education,Wuhan 430063,China
Inner explosion in the broadside protective structure of war-ship will cause severe damage,and numerical simulation is one of the most effective ways to analyze the damage condition of structure under explosive loading.Simulation of cabin structure under inner explosion involves the propagation of shock wave,coupling between multiple flow fields with structure,and distortion and failure of the cabin.A numerical study is performed based on MSC-Dytran software.Further investigation shows that the cutout on bulkhead is useful to reduce the stress localization in cabin corner and thus provides protection to cabin structure.Fragments due to explosive can have a secondary destroy to the cabin structure.
cabin structure;multiple euler-lagrange couple;shock wave;re-produced fragments
U661.43
A
1673-3185(2009)04-07-05
2009-03-24
国防基础研究项目,资助编号(A1420080184)
孔祥韶(1983-),男,硕士研究生。研究方向:海洋工程结构现代强度分析的理论和计算方法E-mail:griansmile@163.com
吴卫国(1960-),男,教授,博士生导师。研究方向:结构动力响应与计算机仿真

