提升操作活动的价值

吴汝萍　刘绪佳

实施新课程后，教师已充分认识到操作活动的重要性，能积极组织学生进行相关的操作活动。但是，反观课堂中的操作活动，不难发现，很多操作活动有“形”无“质”。其实，我们不仅要关注学生的手是否“动”了起来，更要关注学生的头脑是否“动”了起来，是主“动”还是被“动”。操作了，不等于经历了，只有学生的思维动起来，才能提升操作活动的价值。下面以“圆的周长”这一内容的教学为例，谈谈自己的做法与思考。

一、 让学生明确操作的目的与方向

很多老师在教学“圆的周长”时，都是按教材意图，让学生按部就班完成一些指令性的操作。至于开始为什么要测量圆的周长和直径，为什么要算出周长与直径的商，学生不得而知，只能为操作而操作。学生的体验既难丰富，更难深刻。笔者在教学这部分内容时，首先注意让学生明确操作的目的与方向

师：我们已经会求正方形、长方形的周长，正方形、长方形的周长与什么有关？有怎样的关系？

生：正方形的周长与边长有关，是边长的4倍。

生：长方形的周长与长加宽的和有关，是长与宽和的2倍。

师：这节课我们来研究圆的周长。为了确定研究的方向，我们先猜测一下，圆的周长可能与什么有关呢？

学生都猜测圆的周长与半径或直径有关。

师：大家都猜测圆的周长与圆的半径或直径有关，为什么呢？

生：半径的长度决定了圆的大小，半径越长，圆就越大，圆的周长也就越长。

师：那我们就先研究圆的周长与直径之间的关系。大家想怎么研究？

生：想办法量出圆的周长和直径，算出圆的周长与直径的差，看看差是不是固定的。

师：这位同学想研究圆的周长与直径的差是不是一个固定值，你们还想怎么研究？

生：正方形的周长是边长的4倍，也许圆的周长与直径之间也存在着倍数关系，所以我想量出一些圆的周长与直径，分别用周长除以直径，看看商是不是固定的值，如果商是固定的值，说明圆的周长与直径之间就有倍数关系。

师：圆的周长是条曲线，测量很不方便，如果能研究出圆的周长与直径之间的关系，就能得到圆的周长计算公式。那我们就可以利用公式计算出圆的周长，那就方便多了。

先引导学生猜测圆的周长与圆的什么有关系，在学生确定研究圆的周长与半径或直径的关系后，再引导学生确定研究的方法，这样就使后面的动手操作具有一定的目的性和方向性。在学生动手操作前，教师要让学生知道“做什么”，“怎么做”以及“为什么要这么做”，这样才能有效引导学生进一步进行深刻的体验和深入的探

究。

二、 给足学生操作的时间与空间

在“圆的周长”教学中，一位教师从我国古代数学著作《周髀算经》中关于“周三径一”的记载入手。

师：我国古代数学著作《周髀算经》中有“周三径一”的记载。你知道“周三径一”的意思吗？

生：直径是1份，周长是3份。

生：周长是直径长度的3倍。

师：你们都认为这个“径”是指直径，而且都认为周长是直径长度的3倍，为什么不认为周长是半径长度的3倍？

生：从图1中可以看出，周长应该是直径长度的3倍，不可能是半径长度的3倍。

师：那圆的周长是不是就是直径的3倍呢？你们看老师在圆内画一个等边三角形（如图2）。这样的等边三角形在这个圆里到底有多少个呢？

生：有6个。

教师随即在圆里画出另外5个等边三角形，如图3。

师：现在你觉得周长正好是直径长度的三倍吗？

生：不正好。曲的线要比直的线长，所以周长要比直径长度的三倍还要多一点。

师：这个3倍多一些的数到底是多少呢？

教师直接介绍圆周率，并推导圆的周长公式。

上面的教学中，从“周三径一”入手，伴随适当的图示与学生的思考，使学生清晰地认识到“圆的周长是直径的3倍多点”这一重要结论。此教学环节是有意义的，且富有创造性，但是，如果在此基础上，教师能再引导学生动手操作，具体经历探究“圆的周长是直径的3倍多多少”的过程，则会锦上添花。

三、 让学生选择适宜操作的材料与方法

在教学中，要注意引导学生学会“选择”，选择可以执行的操作材料，选择可执行的操作方法。

师：要想获得比较准确的数据，选择什么样的材料以及什么样的方法非常重要。现在，我们要研究圆的周长与直径的关系，需要找一个圆测量出它的直径和周长，你想选择什么样的材料，怎样有效测出圆的直径和周长？

生：我选择一元硬币，用尺量出它的直径，再将硬币从直尺上的零刻度线开始滚动一周，这样就能知道一元硬币的周长。

生：我用硬纸板做了一个直径是4厘米的圆，用丝带沿这个圆裹一圈，圆的周长就是所裹丝带的长度。用尺量一下丝带的长度，就知道了这个直径4厘米的周长。

生：这个透明胶带就是一个圆，直径可以直接用尺量出来，量它的周长也容易。只要将胶带撕下一圈，拉直后量一下它的长度，就这个圆的周长。

师：要想研究圆的周长与直径是否存在某种关系，只研究一个圆行不行？为什么？

生：不行，要多研究几个圆，这样才好比较，才能证明是不是规律。

师：说得非常有道理，一定得多研究几个圆才行。

生：每个同学只要研究一个不同的圆就可以了，因为全班有这么多同学，也就是研究了好多的圆，只要把大家的结论汇总就能得出相关的结论。

师：看来相互合作可以省不少事情，这就是人多智慧多，人多力量大。

教学中，学生选取简便易行的材料，并注意不断优化操作方法，就能使后续的动手操作活动具有“可操作性”，从而促进操作活动有序、高效地开展，提升了课堂教学的效率。

四、 让思维在操作过程中内化与提升

动手操作不是简单的“动手活动”，而应该提升数学思考，努力把外显的动作活动与内隐的思维活动紧密联系起来，使之成为“思维的动作”和“动作的思维”。

师：你测量出的圆的直径是多少？周长是多少？为了得到准确的数据，请大家尽可能多测量几次。

学生测量完后，一一填在表格中，再让学生用计算器算一下圆的周长除以直径的商以及圆的周长减去直径的差：

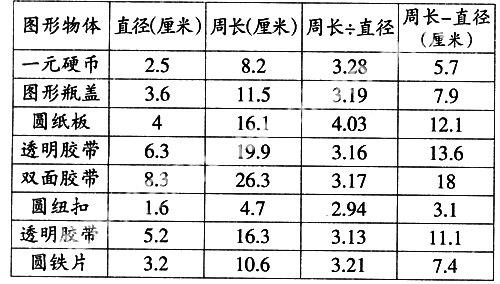
师：观察表中的数据，你发现了什么？

生：圆的周长与它直径的差没有什么明显关系，但圆的周长与它直径的商好像很接近。

生：不管大圆还是小圆，大部分的商都是3倍多一点，只有两个不是。

师：只有两个不是，是什么原因造成的呢？

生：商应该都是3倍多一点，可能是这两个同学的数据测量错了。

师：我们大家一起帮他们重新测量一下。

原先学生是借助丝带测量直径4厘米圆的周长，因为拉的松紧程度不同，所以差异较大。重新测量后，周长是12.8厘米，周长除以直径的商是3.12，差是8.8厘米。

师：看到这个数据，你又猜想到了什么？

生：我猜想纽扣的周长也测量得不准，商应该也是3倍多一点。

生：圆的周长除以直径的商不是整倍数，但都是3倍多一点。

师：根据这些数据，估计一下，圆的周长除以它直径的商大约是3倍多多少?

生：我猜想圆的周长除以它直径的商大概在3.2左右。

师：大家的猜想很有道理。你们听说过圆周率吗？关于圆周率，你们知道些什么？

生：圆周率就是，等于3.14。

生：圆周率是祖冲之发现的。

师：你们知道圆周率具体是什么意思吗？

大多数学生摇了摇头。

师：实际上，我们今天就经历了探索圆周率的过程。任何一个圆的周长除以它的直径的商都是一个固定的数，人们就把这个固定的数叫做圆周率，用字母表示。是个无限不循环小数。早在1500年前，我国数学家祖冲之就计算出圆周率约在3.1415926和3.1415927之间，成为世界上第一个把圆周率的值精确到6位小数的人。

师：日常在计算时，一般将保留两位小数，取它的近似值3.14。

师：刚刚这位学生测量这枚纽扣的周长时，是将纽扣放在桌上滚动的，因为纽扣比较小，实在是不容易操作，所以误差会很大。现在知道了圆周率，你们能推算出这枚纽扣的周长吗？

生：用1.6×3.14≈5.02（厘米）

师：为什么这样算？

生：因为圆的周长÷直径=圆周率，所以圆的周长=圆周率×直径。

师：这位同学由圆周率推想到了圆的周长公式，你还能想到什么？

生：周长÷圆周率=直径。

生：圆的周长=圆周率×半径×2。

操作不仅是为了让学生获得活动经验和相关知识，还应让学生学会自主探究和数学思考。让学生在操作的过程中关注数学的本原，回归数学的本质，使动手操作充满逻辑的力量。