运用现代教育技术 提高课堂教学效率

唐金海

《数学课程标准》(修订稿)明确指出：“数学课程的设计与实施应根据实际情况合理地运用现代信息技术，要注意信息技术与课程内容的有机结合。要充分考虑计算器、计算机对数学学习内容和方式的影响以及所具有的优势，大力开发并向学生提供丰富的学习资源，把现代信息技术作为学生学习数学和解决问题的强有力工具，致力于改变学生的学习方式，使学生乐意并有更多的精力投入到现实的、探索性的数学活动中去。”下面结合《相遇问题》几个教学片断谈一谈“如何运用现代教育技术CAI手段，增强数学学习的趣味性、探索性，提高数学课堂教学效率？”

片断一：模拟生活情景，激发求知兴趣

（课件出示：一条直线，两个人）

师：两人在同一直线上行走，可能会有几种不同的情况？每种情况的运动结果怎样？

生1：两人沿直线面对面走，最终两人走到了一起。

师：这种运动方式，我们称为“相向运动”，运动结果是两人“相遇”。

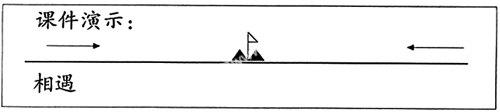
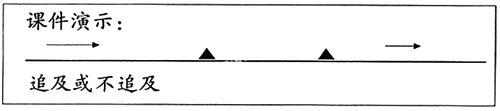
生2：两人沿直线朝同一个方向走。如果后面一个人走得比较快，那么，结果是后一个人追上前一个人；如果后面一个人走得比较慢，那么，结果是两人之间的距离越来越远；如果两人速度一样，那么，两人将始终保持这段距离。

师：这种运动方式，我们称为“同向运动”，运动结果是“追及”或“不追及”。

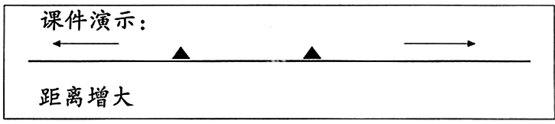
生3：两人沿直线背对背走。运动结果是两人之间的距离越来越大。

师：这种运动方式，我们称为“背向运动”，运动结果是两人之间距离增大。

师：两人在一条直线上运动，有三种基本情况。这节课，我们重点研究第一种情况——相遇问题。（揭示课题）

瑞士著名心理学家皮亚杰指出：“儿童是有主动性的人，他的活动受兴趣和需要的支配，一切有成效的活动须以某种兴趣作为先决条件。”案例中，教师首先抛出“两人在同一条直线上行走，有几种不同的情况”这一开放式的问题，当学生凭借自己的回忆思索描述出三种基本的运动形式时，教师巧妙利用CAI动态画面演示，激活了学生对生活画面的静态储存，引发了学生对生活经验的搜索与整理，激起了学生的数学学习兴趣，自觉建立起“经验”与“知识”的联系，从而较好地找到了知识的生活原型，明确了相遇问题的外部特征，为顺利把握其内在结构作好了初步的铺垫。

片断二：突出认知重点，准确提炼信息

（出示例题：小明和小王同时从甲乙两地相对走来，小明每分钟走60米，小红每分钟走55米，经过4分钟相遇。甲乙两地的路程是多少米？）

师：根据题目描述的情景，请你选择正确的运动方式。

师：你觉得哪一种运动方式是符合题意的？

生1：我认为第三种运动方式符合题意。因为题中描述的情景是“两人同时出发”，第一、二两种方式违背了这一要求。

生2：因为第三种方式两人是同时出发的，所以第三种符合题意。

师：所以，你觉得理解题意时应特别关注哪一个词？

生合：同时。

师：好！请同学们再次配乐欣赏正确的运动方式，再次体会“同时”的含义。

国外众多认知心理学家的大量研究表明：儿童对问题情境的表征或者说对题文的理解，在解决问题中起着关键的作用。因此，采取有效的手段，帮助学生正确领会题目含义，是解决问题的首要任务。相遇问题的理解中，“同时”是重点词，它预示着两人从出发到相遇经过的时间是相等的，因此，理解“同时”意义重大。对此，教师紧紧围绕“同时”进行了两个层次的课件演示：第一层次是在判断中突现“同时”。课件先演示三种不同的运动方式，让学生结合自己对题意的理解进行判断选择，从中突出“同时”这一认知重点。第二层次是在再现中强化“同时”。在学生正确选择运动方式的基础上，课件再次配乐演示正确的运动方式，强化题目重点，最终突破题意理解上的障碍。这两个层次的演示，层层推进，逐步深入，既循序渐进，又一气呵成。

片断三：强化知识表象，分解知识疑难

（学生通过分析数量关系，已发现一种计算方法：60×4+55×4）

师：除了这种方法，还有别的解答方法吗？

（学生或独立思考，或讨论交流）

生1：还可以用（60+55）×4进行解答。

师：你能具体说明这种算法的思路吗？

生1：因为两人是同时出发相对而行，所以，走1分钟两人之间的距离就缩短（60+55）米，4分钟后相遇，就缩短了（60+55）×4米，也就是甲乙两地的路程。

师：你们听懂了吗？

生：……

（学生们有的眉头紧缩，有的低头沉思，显然对这一解法的理解陷入困境）

师：看来，很多同学理解起来还存在一定的困难。这样吧，你可以针对（60+55）×4这个算式进行提问，让计算机帮你解答，好吗？

生2：我想问的是（60+55）表示什么意思？

师：请看演示。看完后，谁能说说（60+55）表示什么意思？

生3：（60+55）表示1分钟两人之间缩短的距离。

生4：（60+55）表示两人1分钟共走的路。

生5：（60+55）表示两人速度的和。

师：我们可以将（60+55）称为“速度和”。谁还想提其他的问题？

生6：我想问的是为什么（60+55）要乘以4？

师：请看演示。看完后请同学解释。

生7：“×4”的原因是两人每分钟走（60+55）米，4分钟就走（60+55）×4米。

生8：“×4”的原因是两人每分钟走（60+55）米，从出发到相遇一共行了4个（60+55）米，所以是（60+55）×4。

师：同学们说得很好！谁能完整地描述这种方法的思路。

表象在数学教学过程中起着积极的桥梁作用，学生理解一个概念、掌握一种方法，都要通过实物、模型或图形建立牢固的“表象”。在此基础上尽量摆脱形象束缚，顺利地过渡到抽象的数学知识，形成新的认知结构。表象的强化过程实际上就是突出重点、分散难点的过程。理解“速度和”的意义，是本节课学习的难点。案例中，教师精心设计了一个学生质疑、课件释疑的课堂情境，使知识疑难的解决过程生动、新颖而有效。教师应用课件控制自如、可放可停的特点，将学生看来完整的运动过程进行细致的解剖和微格的展示，使“速度和”的概念在“分解—递进”的演示过程中，逐步得以展现。这样的演示，紧紧把握对“速度和”概念的理解，形象地展示了知识的发展过程，表象的轨道异常清晰，“速度和×相遇时间=路程”的教学难点被逐步分散，最终得以突破。

作为现代教育技术的CAI手段，具有极丰富的表现力，其画面的逼真性、情节的趣味性和色彩的生动性，非常容易激活生活经验、激发学习兴趣；其化静态为动态、化抽象为形象的技术，能克服人类感官的局限性，弥补传统媒体的缺憾，形象地展示知识发生发展的过程；其交互性强、信息量大的优势能扩大学生的认知空间，优化学生的认知结构。在小学数学教学中，合理运用现代教育技术手段，能有效地突破教学难点、突出教学重点，提高数学课堂教学效率。■