示意图的形成要与学生的思维过程同步

王庆明　邢付元　王友胜

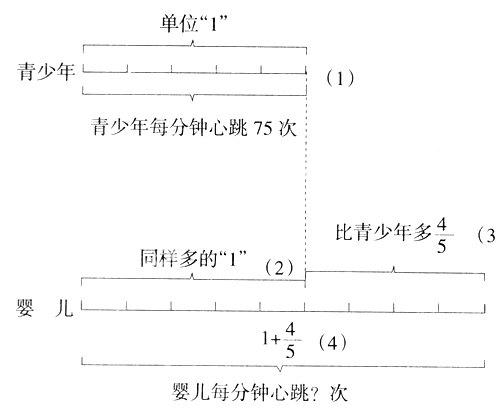
一次听课，教学内容是人教版数学十一册第21页的分数应用题例3:“人心脏跳动的次数随年龄而变化。青少年心跳每分钟约75次,婴儿每分钟心跳次数比青少年多4/5。婴儿每分钟心跳多少次?”由于学生初次接触这样比较复杂的分数应用题,一般需借助示意图才能理清题中的脉络。可执教教师因操之过急,只让学生在初步感知题意的基础上,就一次性地搬出了教例中的“成品图”,结果使大部分学生弄不清数量关系,思维受阻,列不出算,对所授内容不感兴趣,教师也陷入了尴尬的境地.

出现这样情景的根本原因是执教者不能根椐小学生的思维特点，将例题中的示意图随着学生对题意的理解和数量关系的分析,而逐步地、分层次地展现在学生面前，导致了图示形成过程与学生分析思维过程出现了“断层”。

在集体备课会上，大家一致认为,示意图的形成过程,一定要与学生的思维过程同步,与学生的思路紧贴,成为启动学生思维的纽带。提前形成或延后形成都将会阻碍学生的思维发展,失去图示应有的功能。经过反复讨论后我们提出,依小学生的思维特点,此题示意图的形成过程可分三步进行教学:

第一步，抓住关键

通过引导学生对关键句“婴儿每分钟心跳次数比青少年多4/5”的理解,可将青少年心跳次数看作单位“1”，首先画出一条线段表示青少年心跳次数（如图所示⑴）。同时还必须让学生知道，婴儿每分钟心跳次数肯定比青少年多。那么如何引导学生画出另一条线段表示婴儿每分钟心跳次数，也就成了学生解答此题的关键所在。

第二步，突破难点

继续引导学生对“婴儿每分钟心跳次数比青少年多4/5”这个句子进行分析，提出这样几个问题让学生思考:

1.表示婴儿每分钟心跳次数的线段,比表示青少年每分钟心跳次数的线段是长些还是短些？使学生体会到:表示婴儿每分钟心跳次数的线段,除了有表示青少年每分钟心跳次数的线段同样多的外,还有比青少年多4/5的线段，接着便可画出第二条线段，标上“与青少年每分钟心跳次数同样多的线段”（如图所示⑵）

2.如何确定表示婴儿每分钟心跳次数的线段长度？引导学生讨论交流试画:可先将青少年每分钟心跳次数的线段平均分成五份,再在与青少年每分钟心跳次数的线段同样多的基础上,多画出青少年每分钟心跳次数的线段中的四份。使学生体验到:这就是表示婴儿每分钟心跳次数比青少年多出的4/5。（如图所示⑶）接着让学生观察得出,图上⑵和⑶合起来才是表示婴儿每分钟心跳次数的线段。如下图所示:

第三步，揭示规律

通过对以上示意图的整体观察、比较和分析,进一步引导学生找出与未知量相对应的分率,弄清未知量与已知量的关系。让学生明白：青少年每分钟心跳次数是5个1/5，婴儿每分钟心跳次数比青少年多4/5，婴儿每分钟心跳次数就相当于青少年的9个1/5，即1＋4/5（如图所示⑷）。求婴儿每分钟心跳多少次，也就是求75次的（1＋4/5）是多少,根据分数乘法的意义,引导学生独立列出算式75＋75×4/5或75×（1＋4/5）。

后来仍让这位教师按以上步骤在另一班试教,其教学效果比预料的还要好。教师边讲边一步步地引导学生画出示意图,使题中的数量关系分步地、动态地呈现在学生面前，与学生的思维展开过程紧密配合，促使学生由具体形象思维向抽象逻辑思维发展，较好地完成了教学任务，学生的思维能力在示意图形成的同时也得到了同步发展。