频数与频率的应用
徐 艳
频数就是所要考察的每个对象出现的次数,频率就是每个对象出现的次数与总次数的比值(或百分比).频数、频率与总次数存在的关系是:(1)频数之和等于总次数;(2)频率=频数/总次数.在实际生活中,许多问题涉及频数与频率的计算问题.
例1小华和小明分别是七(1)班和七(2)班的同学,他们在各自班级举行的最受欢迎的同学评比中,小华得到了38票,小明得到了30票.小广由此断言,小华受欢迎的程度比小明高.你同意小广的观点吗?请用频数与频率的知识说明理由.
分析:要用频数与频率的有关知识比较小华、小明两同学受欢迎的程度,实际上是比较两个同学得票的频率的大小,为此,需要知道两个同学得票的频数以及班级总的参加人数.
解:小广的观点不正确.从得票数来看,小明的少些,但受欢迎的的程度并不依赖于得票的多少,而是取决于得票的频率的大小.由于各班的总人数不知道,所以无法准确地计算出他们得票的频率.所以无法比较两个同学受欢迎的程度.
比较两个同学在班内受欢迎的程度,不应该从得票频数方面考虑,而应从得票频率的大小出发来进行比较与探究.
例2七(3)班举行投票选举班主任助理活动,已知小强和小亮是两名候选人,要在这两名同学中选举一名同学,全班有58人参加投票,投票情况如表1.
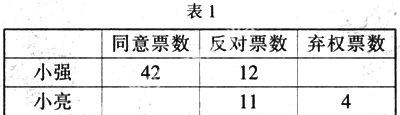
(1)小强得到的弃权票的频数是____,同意票的频率是____;
(2)小亮得到的同意票的频数是____,同意票的频率是____;
(3)这两个同学谁会当选?
分析:由于全班有58人,所以“同意票数+反对票数+弃权票数=58”,要求出其中一种意见的票数,只要用总票数减去另外两种意见的票数即可.
解:(1)小强得到的弃权票数为58-42-12=4,同意票的频率为42/48=21/29.
(2)小亮得到的同意票数为58-11-4=43,同意票的频率为43/58.
(3)根据同意票的频数或频率可知,小亮得到的同意票较多(或同意票的频率较大),所以小亮当选.
频数、频率在实际问题中应用广泛,同学们应熟练掌握频数、频率的关系以及它们的计算方法.
例3一粒木质中国象棋子“兵”,它的正面雕刻一个“兵”字,它的反面是平的,将它从一定高度下掷,落地反弹后可能是“兵”字面朝上,也可能是“兵”字面朝下.由于棋子的两面不均匀,为了估计“兵”字面朝上的频率是否随着实验次数的增多而趋于稳定,某实验小组做了棋子下掷实验,实验数据如表2.

(1)请将表中数据补充完整;
(2)如果实验继续进行下去,根据表中的数据,这个实验的频率将稳定在一个固定的值附近,请你估计这个固定值是多少.
分析:本题是一道与实验频率有关的实际问题,根据频率、频数以及实验次数之间的关系,可计算出“兵”字面朝上的相应的频数和频率.根据多次实验后的频率,可以估计频率的稳定值.
解:(1)当实验次数是40时,对应的频率是0.45,所以“兵”字面朝上的频数是40×0.45=18;当实验次数是120时,“兵”字面朝上的频数是66,相应的频率是66÷120=0.55.
(2)根据表中数据可以发现:如果继续实验,实验的频率将稳定在0.55左右.
实验的次数越多,相应的频数也就越大,而实验的频率则趋于稳定.根据频率的稳定性,可以作出决策并解决相应的实际问题.
(责任编辑:田心红)
- 中学生数理化·七年级数学华师大版的其它文章
- 努力与梦想
- 把握中学时代的黄金时光
- 让数据说话 传递有用信息
- 做数据收集和整理的小能手
- 看奥运,识统计图
- 双统计图问题浅析

