一种抑制反作用轮低速摩擦对卫星姿态扰动的方法*

丁建钊

(1.北京控制工程研究所，北京 100190； 2.空间智能控制技术国家级重点实验室,北京 100190)

1 引 言

在现代卫星的姿态控制系统中，反作用轮占据着重要的地位。在三轴稳定卫星的控制系统中，许多采用由3个轻型反作用轮正交安装组成的控制系统，该系统具有结构简单、成本低、精度高和灵活机动的特点，可以满足一些高性能对地观测卫星的任务要求。但是由于卫星在轨道运行期间受到周期性的外干扰力矩，反作用轮的角动量会从正值变为负值，或者相反。当反作用轮转速过零时，由于摩擦力矩相对于控制力矩较大，会对卫星姿态产生较大的影响，因此必须对反作用轮转速过零时低速摩擦产生的扰动进行抑制。

目前国内外学者已经提出了几种解决方法，其中具有代表性的两种解决方法是：(1)利用摩擦观测器对反作用轮低速摩擦进行估计并补偿[1～3]；(2)从姿态控制系统设计角度入手，设计鲁棒性好的控制器来抑制低速摩擦对卫星姿态的影响[4～6]。本文主要从姿态控制系统设计角度入手，讨论鲁棒性强的基于特征模型的全系数自适应控制器对于低速摩擦的抑制问题。

2 反作用轮的低速摩擦特性

除了受飞轮电机的电磁驱动力矩Tm外，反作用飞轮还受到轴承摩擦力矩Tf的影响，二者的合力矩支配着反作用轮的转动，同时该合力矩的反作用力矩就是对星体的控制力矩。姿态控制器所施加的控制力矩仅是其中的一部分，即电磁驱动力矩的反作用力矩，二者之间的关系如式(1)所示。

Tc=Tm-Tf

(1)

(2)

其中，u(t)为电机驱动电压，i(t)为电机电驱电流，u(t)由控制器根据卫星姿态偏差确定。

美国学者于1968年通过理论分析和实验提出了Dahl模型[1]，该模型反映了摩擦特性的迟滞效应和库仑摩擦力矩，已被广泛应用于反作用轮姿态控制系统的设计。当考虑粘性摩擦和Dahl模型时，力矩式反作用轮低速摩擦模型如图1所示。

图1 反作用轮的低速摩擦特性

由图1，可以看出摩擦力矩与转速满足下式[1]：

(3)

模型中各参数意义及取值为[2]：

转动惯量J=0.023 kg·m2,电机电枢的电感L=0.001079 H，电机电枢的电阻R=0.54 Ω，反电势系数Ke=0.062Vs，电机转矩系数Km=0.062N·m/A，阻尼系数D=0.009N·m·rad,轴承静止斜坡参数β=12200(N·m·rad)-1，库仑摩擦力矩Tf 0=0.014N·m。

3 基于特征模型的黄金分割自适应控制

所谓特征建模，就是根据对象动力学特征和控制性能要求相结合进行建模，而不是仅以对象精确的动力学分析来建模[7]。其特点为：模型形式应比原对象动力学方程简单，工程实现容易、方便；特征模型与高阶系统的降阶模型不同，它是把高阶模型的有关信息都压缩到几个特征参量之中，并不丢失信息，一般情况下特征模型用慢时变差分方程描述，根据系统的输入输出通过参数估计算法估计出时变差分方程的参数，设计简单。

3.1 建立对象的特征模型

在控制器设计时不考虑系统摩擦力矩的影响。当反作用轮的安装方向与卫星俯仰轴的方向相同时，系统的方程为：

(4)

而由反作用轮的动力学知：

u(t)=-uc

(5)

其中uc为姿态偏差控制所需要的控制量。

取系统的状态变量为：

则系统写成状态空间形式为：

(6)

其中：

C=[1 0 0 0] ,D=0

则从uc到θ的传递函数为：

G(s) =-C(sI-A)-1B+D

(7)

对其传递函数进行分解，可得到如下形式：

(8)

根据文献[7,9]可知，在满足一定采样周期的条件下，当要实现位置保持或位置跟踪控制时，其特征模型可用一个二阶时变差分方程形式来描述：

y(k+1)=f1(k)y(k)+f2(k)y(k-1)+

g0(k)u(k)+g1(k)u(k-1)

(9)

并且满足：

(1)上述方程的系数是慢时变的；

(2)系数的范围可事先确定；

(3)动态过程中，在同样输入情况下，特征模型的输出与实际对象输出是等价的(适当选取采样周期可保证输出误差在允许范围内)；稳态情况下输出相等；

(4)当静态增益D=1时，稳态情况下系数之和等于1；

推导其系数，可得：

f1(k)=2-Δt(a1(y)+a2(y)),

f2(k)= -[1-Δt(a1(y)+a2(y))+

Δt2a1(y)a2(y)] ，

g0(k)=Δt(K1+K2)+Δt2k6,

g1(k)= -Δt(K1+K2)+Δt2[K1a2(y)+

K2a1(y)]。

其中Δt为采样周期，其推导过程和参数的具体意义及取值范围详见文献[9]。

当对象为最小相位系统或某些弱非最小相位系统时，在工程上为了简化方便，一般只取一个g0(k)，即：

y(k+1)=f1(k)y(k)+f2(k)y(k-1)+

g0(k)u(k)

(10)

3.2 基于特征模型的自适应控制[7～9]

(1)特征模型参数辨识

将特征模型写成：

y(k)=φT(k-1)θ(k)

(11)

其中：

φ(k-1)=[y(k-1)y(k-2)u(k-1)]T,

θ(k)=[f1(k)f2(k)g0(k)]T。

参数估计采用带有遗忘因子的递推最小二乘法：

(12)

(2)控制律设计

根据本系统的特点，设计如下控制律：

a)线性黄金分割自适应控制律

(13)

其中:

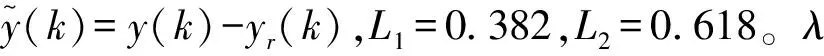
b)逻辑微分控制律

ud(k)=Kd[y(k)-y(k-1)]

(14)

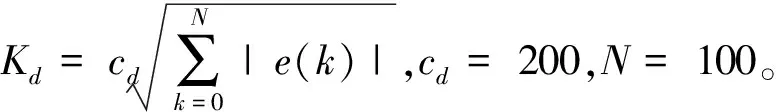
c)逻辑积分控制律

(15)

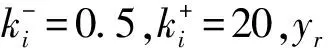
总控制律为:

u(k)=-[ul(k)+ud(k)+ui(k)]

(16)

控制器的框图见图2。

图2 全系数自适应控制系统示意图

4 仿真结果及其分析

考虑采用反作用轮控制的卫星俯仰轴姿态控制，取俯仰轴的转动惯量为1000kg·m2。环境干扰力矩考虑重力梯度力矩和气动干扰力矩，具体为：Tey=A0(1.5sinω0t+3cosω0t)，其中幅值为A0=10-5N·m，轨道角速度为ω0=0.001059rad/s。使用本文设计的基于特征模型的全系数自适应控制器的结果见图3。

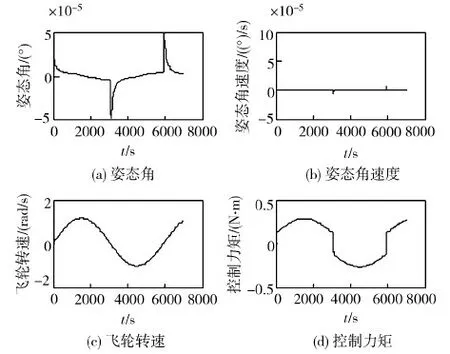
图3 全系数自适应控制器的控制结果

与PID控制的比较结果见图4和图5。

图4 姿态角变化的比较

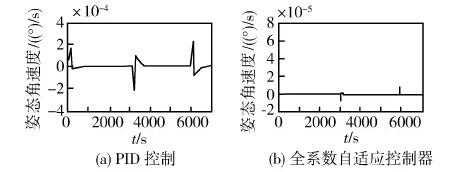
图5 姿态角速度变化的比较

图6 飞轮转速变化的比较

根据仿真结果，可以得出以下结论：

(1)从图4中可以看出，在全系数自适应控制器控制下，低速摩擦对卫星本体Y轴的姿态角产生最大0.000049°的姿态扰动，远小于PID控制时的姿态扰动量，从而可以提高姿态控制精度。

(2)从图5中可以看出，在全系数自适应控制器控制下，低速摩擦对卫星本体Y轴的姿态角速度产生最大为0.7×10-5(°)/s的姿态扰动，这也远小于PID控制时的姿态扰动量，从而提高了姿态的稳定度。

(3)从图6中可以看出来，在全系数自适应控制器控制下，Y轴的飞轮也会出现转速过零现象，但此时其转速被低速摩擦捕获时间比PID控制的捕获时间大大缩短，不超过10s，而且过零时的转速跳变幅度也变小，只有0.008rad/s，从而减小了对卫星姿态的影响。

上述各种方法的比较见表1。

表1 PID控制与全系数自适应控制器的比较

5 结 论

从以上分析可以看出，全系数自适应控制器可以看成是一个变参数的PID控制器，可以随着系统的状态随时改变控制器的参数，从而可以达到较高的精度。而PID是线性反馈，没有根据系统的状态做相应的改变，从而达不到很高的精度。

从仿真中也可以看出，在没有摩擦补偿观测器的情况下，全系数自适应控制器可以大幅度地减弱反作用轮转速过零时的抖动现象，提高卫星姿态控制的精度及稳定度，从而可以提高对地观测卫星的对地观测能力。