地球辐射波动对摆动扫描式红外地球敏感器测量误差的影响分析

王 韬，王 平，刘旭力

(北京控制工程研究所，北京 100190)

1 引 言

摆动扫描式红外地球敏感器已被广泛地用于卫星对地姿态测量。为了获得更高的测量精度，其工作波段一般选在14～16.25μm的红外波段，这也是CO2的吸收波段。由于季节、地理位置等因素的影响，地球在该波段的辐射不均匀，这就会给摆动扫描式红外地球敏感器的测量结果带来误差，称为地球辐射误差，它是摆动扫描式红外地球敏感器系统误差的主要来源之一。以往国内的摆动扫描式红外地球敏感器很少用在倾斜轨道上，这项误差一直没有引起重视，国内也没有深入开展过对这项误差的分析。本文结合法国SODERN公司的地球红外辐射模型，对工作在倾斜轨道上的摆动扫描式红外地球敏感器的地球辐射误差进行了分析和仿真。

2 摆动扫描式红外地球敏感器的工作原理

为了描述简洁，下文用“地球敏感器”代替“摆动扫描式红外地球敏感器”。图1描述的是其姿态测量几何关系，XOY是与卫星固连的地球敏感器坐标系，X轴和Y轴分别与卫星的滚动轴和俯仰轴平行，地球敏感器的复合视场由4个射束型的基本视场组成，它们沿图1所示的轨迹扫描红外地平，4个基本视场运动到中点位置A、B、C、D的时刻称为地球敏感器的基准时刻。4个基本视场的地平穿越点分别为A＇、B＇、C＇、D＇，对应的时刻为地平穿越时刻，零姿态情况下，地平穿越时刻与地球敏感器的基准时刻一致。当卫星有姿态偏差时，各基本视场的地平穿越时刻与地球敏感器的基准时刻不再一致，而存在时间差。地球敏感器上的信号处理电路分别对这4个时间差进行处理得到卫星的俯仰和滚动姿态[1]。

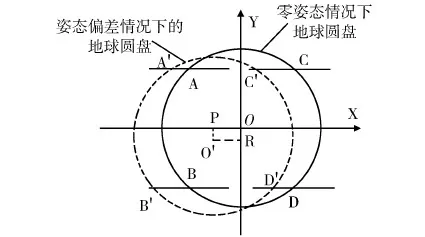
图1 摆动扫描式红外地球敏感器的姿态测量几何关系

图2是地球敏感器的基本工作原理框图，地球敏感器的光学系统对地球和背景空间的红外辐射进行检测，输出类似梯形的地球波；光学系统头部模拟通道的前置放大电路、微分电路和穿越处理电路对地球波进行放大和微分，并提取出代表姿态信息的地平穿越脉冲；利用地平穿越脉冲、基准信号、时钟信号和逻辑控制信号，姿态处理环节按一定逻辑关系的组合处理出几路脉冲数与姿态偏差成比例的脉冲串，再经过俯仰、滚动姿态输出单元对几路脉冲串的处理，即可得到幅值与姿态角成正比的直流电压信号V。

理想情况下，地球敏感器的光学系统输出的地球波应该是矩形波，但是由于红外地平圈附近的红外辐射亮度由内向外是逐渐减小的，因此地球敏感器输出的实际地球波的形状和梯形相似。并且随着地球敏感器视场穿越点处的地球红外辐射亮度的不同，地球波的上升沿上升的快慢程度也不一样。因此，即使当卫星的姿态为零时，由于卫星工作的轨道倾角不同，地平穿越点处的红外辐射亮度也不相同，每个基本视场的地平穿越时刻也不再与地球敏感器的基准时刻重合，就会产生测量误差，这便是地球敏感器的地球辐射误差。而要想对此误差进行分析，一个精确的地球红外辐射模型必不可少。

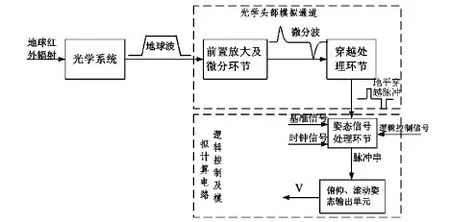
图2 摆动扫描式红外地球敏感器工作原理图

3 地球红外辐射模型

地球在14～16.25μm波段的辐射是一种非常复杂的现象，与地球辐射率、大气传输比、地表温度、云层情况、大气成分以及当地的气象条件都有关系。要想建立一个地球辐射模型，最有效的方法是利用地面气球、探空火箭以及中低轨道卫星等途径做实际飞行测量，积累至少数年的地球红外辐射数据，在此基础上建立地球红外辐射数据库，再利用这些数据对地球红外辐射进行分析并建立模型。目前国内还没有开展过对地球红外辐射模型的系统研究，因此下面给出法国SODERN公司的地球辐射模型[2]。

春季：

夏季：

秋季：

冬季：

其中，T=365.25天；L为地球红外光谱辐亮度，单位是W/(m2·sr·μm)；t-t0为天数，从每年的4月10号开始计算；latitude为纬度，单位是(°)。

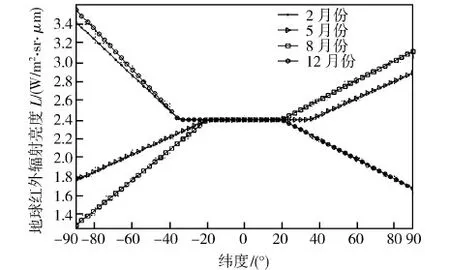
图3 地球红外辐射亮度与季节和纬度的关系

根据辐射模型绘出了2月份、5月份、8月份和12月份地球的红外辐射亮度与纬度的关系曲线，如图3所示，图中负纬度表示在南半球，正纬度表示在北半球。由曲线可以看出，在南半球，5月份、8月份、2月份、12月份地球红外辐射波动梯度依次增大，北半球也是如此，且北半球2月份和12月份的辐射波动基本一致。从南纬20°到北纬20°这一区域内，地球的辐射比较均匀。

地球的红外辐射跟纬度、季节以及时间有关，因此，要分析地球红外辐射的不均匀对地球敏感器视场输出的地球波的上升沿和下降沿的影响，需要先分析地球敏感器扫描时其基本视场与地球面交点的纬度变化规律。

4 地球敏感器的视场运动模型

(1)参考坐标系

为了研究问题方便，引入以下参考坐标系：

a.赤道惯性坐标系(XiYiZi)

坐标原点在地心，Xi轴指向赤道平面与黄道平面的相交节线的升交点(指向春分点)，地球的自旋轴为Zi轴，并以地球自旋角速度的方向为正，Yi轴和Xi、Zi轴组成右手正交坐标系，此坐标系可以近似认为是一个惯性坐标系，用下标i表示。

b.质心轨道坐标系(XoYoZo)

坐标原点在航天器的质心上，由质心指向地心的坐标轴是Zo轴，Xo轴在轨道平面上与Zo轴垂直，指向航天器的速度方向，Yo轴与Xo、Zo轴组成右手正交坐标系。此坐标系在惯性坐标系中是旋转的，用下标o表示。

(2)地球敏感器视场与地球面交点的纬度

地球敏感器的复合视场由4个铅笔射束型的基本视场组成，零姿态情况下，4个基本视场的运动规律如图1所示。为了分析问题方便，每个视场的射束都用一条射线代替，现以视场C为例求在扫描过程中与地球面交点的纬度。

图4 视场C的扫描过程示意图

图4为视场C的扫描过程示意图，其中Oo为卫星质心，Oi为地心。根据SODERN的地球辐射模型，地球敏感器的视场接收到的地球辐射只与纬度、季节和时间有关，因此在分析视场的运动情况时，可以用射线MH近似代表地球敏感器视场C的射束，如图4所示。它与平面XoOoYo的夹角是β，随着β在某一范围内变化，射线MH在与XoOoZo平面平行的平面MPQ中运动以完成对地球的扫描。在质心轨道系中，直线MH的方向数为(cosβ,0,sinβ)，由于卫星远离地球，在求视场C与地球面交点的几何关系中，可以认为M点的坐标是(0,Resinγ,0)，其中γ为视场扫描纬度，Re等于地球半径加上地球周围CO2层的高度。β只是在(0°,90°)范围内的某个区域内变化，因此直线MH的方程为

(1)

地球球面方程为

(2)

式中，r为地球球心与卫星质心之间的距离，联立式(1)和(2)，经化简、整理得

(3)

这是一个关于x的一元二次方程，令其判别式等于零可得

(4)

记

(5)

对于视场C和视场D，当β=β1时，其视场线与地球面相切，对于视场A和视场B，当β=β2时其视场线与地球面相切。设地球敏感器的视场扫描幅值是±α，因此视场C工作时,图4中β的变化范围是[β1-α,β1+α]。

当Δ≥0时，由方程(3)在实数范围内可解出两个值

(6)

那么

(7)

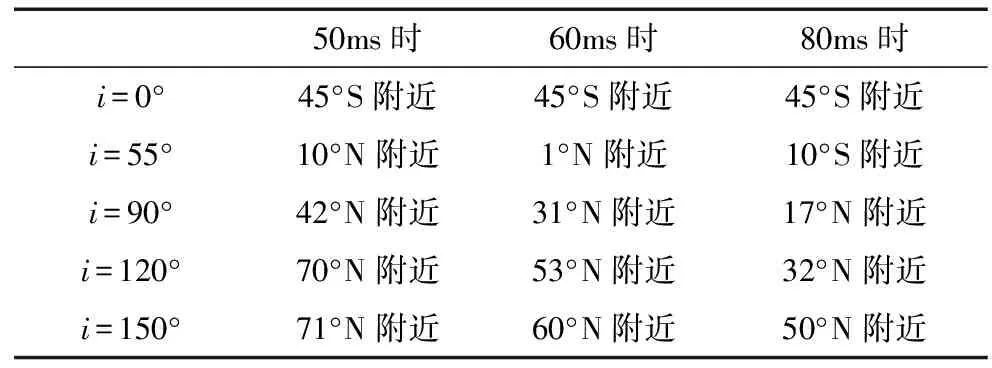
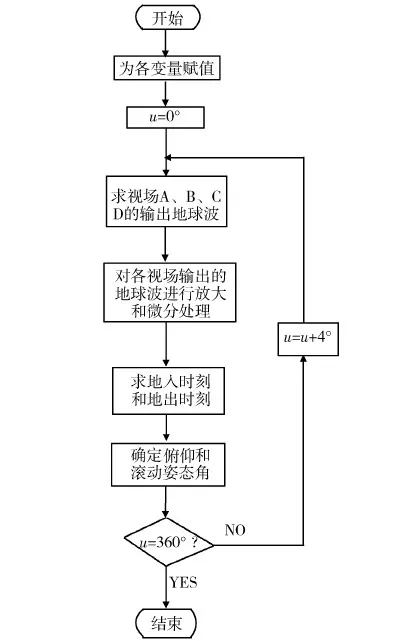
式(6)和(7)是直线MH与地球面两个交点的坐标，其中只有z值小的那个交点有意义。假设z2

(8)

其中，u为轨道平面内从升交点到卫星所在位置的张角，i为轨道倾角，Ω为升交点赤经。所以，点N的纬度φN为

(9)

得到地球敏感器视场扫描处的纬度后，再结合季节和时间，可根据SODERN的地球辐射模型计算出地球敏感器视场接收到的地球红外辐射。根据图2所示的地球敏感器工作原理，视场接收到的地球红外辐射经光学系统、光学头部模拟通道和逻辑控制及模拟计算电路处理，便可得到幅值与姿态角成正比的直流电压信号V。

5 仿真结果及分析

本文对不同轨道倾角时地球敏感器基本视场的输出地球波的上升沿进行了仿真，同时还对地球敏感器在不同季节的地球辐射误差进行了仿真。两次仿真的公共条件如下：卫星轨道高度h为21 500 km的圆形轨道，卫星姿态角为零，地球半径为6378 km，地球周围CO2层的高度为22 km，地球敏感器的视场扫描纬度γ=45°。

(1)地球敏感器基本视场输出的地球波上升沿比较

在公共仿真条件的前提下，对地球敏感器工作在倾角分别为0°、55°、90°、120°和150°的轨道上时的视场C的扫入阶段进行了仿真，仿真时假设卫星处于升交点上，并设当前时间为12月10日，仿真结果如图5。结果显示，当卫星工作在倾斜轨道时，由于轨道倾角不同，地球敏感器的视场C扫入地球的过程中扫到的地球纬度带不同，根据SODERN的地球辐射模型，视场C接收的红外辐射亮度也不相同。因此视场C输出的地球波的最大值以及上升沿上升的快慢程度各不相同。表1所示的是不同轨道倾角时视场C在不同时刻扫到的纬度带，随着轨道倾角的增大，视场C扫到的纬度带由南半球逐渐向北半球过渡。根据SODERN的地球辐射模型，12月份时地球的红外辐射亮度由南半球到北半球是逐渐减小的。因此，当视场C扫入地球之后，轨道倾角越大，探头的输出电压就越小，如图5中所示。对于摆动扫描式红外地球敏感器，其地球波的下降沿与上升沿关于中点时刻对称。

表1 不同轨道倾角和不同时刻视场C扫到的纬度带

图5 不同轨道倾角下视场C的扫入曲线的上升沿比较

不同轨道倾角下视场C输出的地球波的上升沿、下降沿以及最大值各不相同，经过地球敏感器的前置放大及微分电路处理之后，得到的微分波的前沿、后沿以及最大值也各不相同，因此这些微分波对应的地入和地出时刻也各不相同，于是就会产生地球辐射误差。

(2)地球辐射误差的仿真

在公共仿真条件下分别对2月份、5月份、8月份和12月份地球敏感器在55°倾角轨道上一个轨道周期内的地球辐射误差进行了仿真，考虑到仿真时间的长短，u的步长取4°。图6是仿真的程序流程图，图7和图8分别是4个月份的俯仰辐射误差和滚动辐射误差。

图6 仿真程序流程图

表2描述的是卫星工作在此轨道条件下时，星上地球敏感器的4个基本视场扫描到的纬度范围。可见，一个轨道周期内，视场A、C的穿越点大多数都在南半球，且在北半球的部分也在20°N以下。视场B、D的穿越点大多数都在北半球，且在南半球的部分也在20°S以上。由图3知，5月、8月、2月、12月南半球的地球辐射波动依次增大，因此，当用视场A、C的输出确定俯仰姿态时，12月份的俯仰误差最大，最大可达到0.16°，5月份的俯仰误差最小，其最大值也只有0.07°，如图7所示。滚动姿态受地球红外辐射波动的影响比俯仰要小得多，这主要和计算它们的数学算法有关，滚动误差绝对值的最大值约为0.06°，如图8所示。

图7 不同月份的俯仰角辐射误差

图8 不同月份的滚动角辐射误差

6 结 论

本文结合法国SODERN公司的地球红外辐射模型，对摆动扫描式红外地球敏感器在倾斜轨道上工作时的误差进行了分析，通过数学仿真得出了由于地球红外辐射波动造成的俯仰和滚动姿态角的误差曲线。仿真结果表明当摆动扫描式红外地球敏感器工作在55°倾斜轨道上时，地球的红外辐射波动对俯仰和滚动姿态测量造成的误差最大值分别为0.16°和0.06°。

表2 地球敏感器视场扫描到的纬度范围