基于无源性的航天器姿态跟踪控制设计*

霍 伟

(北京航空航天大学第七研究室，北京 100083)

1 引 言

航天器姿态控制是航天控制研究中的重要问题。由于工程中各种复杂因素和工作环境的影响，很难得到航天器动力学参数的准确值并对所受干扰进行精确建模，因此含模型不确定性航天器的姿态控制问题得到广泛研究。主要的方法有自适应控制、变结构控制、鲁棒控制以及这些方法的组合等。

自上世纪80年代末以来，机器人控制领域中基于非线性控制系统理论中无源性原理的自适应控制研究得到很大发展[1,2]。这种方法最主要优点是可以充分利用系统的动力学特性，设计出不依赖加速度测量的自适应控制方案。受这类机器人控制设计方法的启发，基于无源性的刚性航天器姿态控制设计越来越受重视[3～6]，但这类方法的相关文献中一般都没考虑航天器所受的干扰，给实际应用带来不便。

考虑到机器人和航天器都是非线性力学系统，具有共同的力学性质，本文利用机器人研究中发展起来的无源性控制设计理论，针对刚性航天器含惯性参数不确定性和未知干扰力矩的不同情况，在统一的理论框架内设计出多种自适应和变结构姿态跟踪控制律，并给出跟踪误差收敛到零的严谨证明。同时也将一些已有的自适应和变结构姿态控制方法纳入这一理论体系，给予新的理论解释，为今后相关设计提供理论基础。

2 航天器姿态动力学模型及其力学性质

对于可视为刚体的航天器，建立惯性参考系及与航天器固连的机体坐标系，将航天器相对惯性系的姿态用欧拉角q=[φ,θ,ψ]T表示，它的姿态运动学方程为[7]

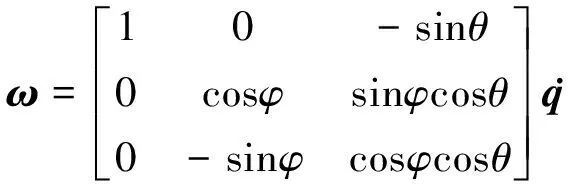
(1)

式中ω为航天器角速度在机体坐标系中的表达式。由式(1)可知：B(q)在|θ|<π/2时可逆，故本文只研究θ在此范围内变化的情况。

设航天器中3个反作用轮的转轴沿机体坐标系各坐标轴安装，其对机体坐标系原点的惯性张量阵在机体坐标系中的表达式是一常值对角阵JR,航天器本体对机体坐标系原点的惯性张量阵在机体坐标系中的表达式是一常值对称阵J,航天器动量矩

H=(J+JR)ω+JRΩ

(2)

式中Ω为反作用轮相对本体的角速度。由动量矩定理可导出航天器姿态动力学方程为[7]

(3)

式中H×为H所对应的反对称叉乘矩阵，u为航天器受到的控制力矩,d为干扰力矩。利用式(1)～(3)可将航天器姿态动力学方程写为

(4)

式中

M(q)=BT(q)JB(q),

容易证明航天器姿态动力学具有以下性质[8]：

1)M(q)是正定阵。

2)若记

JR=diag(JR1,JR2,JR3),

航天器惯性参数p[J11,J12,J13,J22,J23,J33,JR1,JR2,JR3]T，其姿态动力学特性可表为其惯性参数的线性函数,即对任意q,Ω,x有

注1．若航天器是以喷气装置为作动器而没有反作用轮,则以上各式中的JR和Ω均为零,u为喷气装置施加在航天器上的力矩。

3 基于无源性的控制器设计理论

定义1.记R+[0,∞)，函数空间L2定义为

L2中的内积和范数定义为

函数空间L∞定义为

定义2.函数f(t)的截取fT(t)定义为

扩展的L2空间定义为

∀T∈R+}

文献[2]在研究用统一的方法设计机器人无源控制器时证明了以下结果。

引理1.若闭环控制系统具有图1所示的结构，其中算子H1是无源的，算子H2是严格无源的，算子H3是无源的，则输出r∈L2。

图1 闭环控制系统结构

文献[1,2]中用这一引理设计机器人无源自适应控制器的基本原理是:证明算子H1的无源性可由机器人本身的动力学特性保证; 算子H2的严格无源性可用反馈控制器保证; 算子H3的无源性由补偿机器人模型不确定性的自适应控制律保证(当无模型不确定性时这一算子可去掉)。文献[1,2],中通过设计不同的H2和H3,在统一的理论框架内设计出了多种机器人无源自适应控制器。由于航天器与机器人一样是受控的非线性力学系统，所以完全可以借鉴机器人无源控制器设计方法来设计含模型不确定性的航天器控制器。

4 基于无源性的航天器姿态跟踪控制律设计

定义

(5)

取航天器控制

(6)

(7)

为简洁表达,式(7) 中未写出自变量,以下在不会引起误解时均如此处理。式(7)表明闭环系统可用图2所示框图表示。

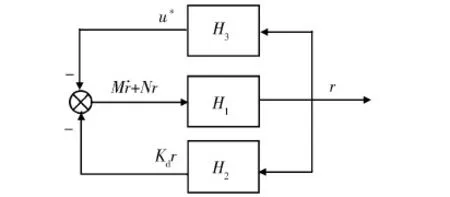
图2 航天器闭环系统结构图

由定义知这表明航天器姿态动力学特性可保证H1是无源的。又易知

其中λm(Kd)是Kd的最小特征值,故由定义知H2是严格无源的。考虑到

这表明用PD反馈可保证H2是严格无源的。

4.1 惯性参数是未知常数且干扰力矩上界未知时的控制设计

这时惯性参数p=[J11,J12,J13,J22,J23,J33,JR1,JR2,JR3]T[p1,…,p9]T是未知常数,记其估计值干扰力矩d=[d1,d2,d3]T满足但是未知常向量。选取控制律(6)中的和参数自适应律如下

(8)

(9)

(10)

(11)

(12)

应用以上两式可算出

由定义知H3是无源的,再由引理1知r∈L2。

定义函数

由M(q)及Γ和E的正定性知v(t)≥0。利用式(4)、(6)、(8)、(11)和(12)可算出沿闭环系统轨线

≤0

这表明沿闭环系统轨线v(t)单调有界,故存在有限极限v(∞),且有

0≤v(∞)≤v(t)≤v(t0)<∞, ∀t≥t0≥0

由上式及v(t)的定义知

定义4.记以s的实系数有理函数为元的n×n阵全体为Rn×n(s)，对于W(s)∈Rn×n(s)，若当s→∞时W(s)的所有元均有界,则称它是正则的; 若当s→∞时W(s)的所有元都趋于零,则称它是严格正则的; 若W(s)是正则的且其所有极点的实部均为负,则称它是指数稳定的。

引理3[10].研究输入-输出系统

由式(5)知r和e间的Laplace变换为

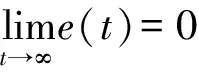
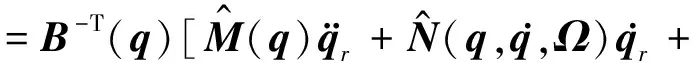
命题1.对于其姿态动力学方程用式(4)表示的航天器,若其惯性参数是未知常数且干扰力矩上界未知时,可用控制律

和参数自适应律(9)和(10)实现对期望姿态的跟踪。

注2．控制律(13)中各项有明确含义:前两项为用惯性参数估计值算出的前馈动力学补偿项,第3项是利用干扰力矩上界的估计值抑制干扰的变结构控制项,第4项是PD反馈项。两个参数自适应律分别实时调节惯性参数和干扰力矩上界的估计值。

注3．与已有控制律相比较可看出：若此时不考虑干扰力矩，即得到文献[11]中的自适应控制律；若在文献[8]的控制律中加入对干扰力矩上界的实时估计，即可得到上述结果；若对文献[12]中干扰力矩上界的估计方法加以修改，也可将其纳入本文的理论框架。

4.2 惯性参数估计误差上界和干扰力矩上界均未知时的控制设计

(14)

(15)

(16)

利用自适应律(15)和(16)可算出

由定义知H3是无源的,再由引理1知r∈L2。

定义函数

命题2.对于其姿态动力学方程用式(4)表达的航天器,若其惯性参数估计误差上界和干扰力矩上界均未知时,可用控制律和参数自适应律(15)和(16)实现对期望姿态的跟踪。

(17)

4.3 惯性参数估计误差上界和干扰力矩上界已知时的控制设计

这时

利用上式可算出

≥0

由定义知H3是无源的。再定义函数

命题3.对于其姿态动力学方程用式(4)表达的航天器,若其惯性参数估计值的误差上界和干扰力矩上界均已知时,可用控制律使航天器实现对期望姿态的跟踪。

4.4 惯性参数和干扰力矩上界均已知时的控制设计

这时也可采用更简单的变结构控制律。取

这时可算出

≥0

命题4.对于其姿态动力学方程用(4)式表达的航天器,若其惯性参数估计值的上界和干扰力矩上界均已知时,可用变结构控制律实现对期望姿态的跟踪。

以上命题1～4的结果均用仿真算例进行了验证,由于篇幅所限,不再详述。

5 结 论

本文基于机器人控制研究中提出的无源性设计方法，用统一的理论方法对含模型不确定性的航天器设计了多种自适应和变结构姿态跟踪控制律，并证明了闭环系统稳定性，为刚性航天器控制器设计提供了理论参考。另外，我们最近的研究表明：对含柔性附件的航天器，也可用这一理论设计出控制律，在实现姿态跟踪的同时，抑制柔性附件的振动，有关结果将另文发表。

最后需要说明的是，本文为叙述清楚做了两点简化：一是只研究了用欧拉角描述姿态的情况,但所述方法对用四元数描述姿态时也完全适用,因为这时航天器姿态动力学也具有文中所述的3个力学性质[13]；二是用PD控制保证了算子H2的严格无源性，实际上使用任何使r和e间传递函数W(s)严格正则且指数稳定的控制(如PID控制等)均可[2]。