利用摆动地球敏感器两个探测器输出的姿态确定
刘新彦
(北京控制工程研究所,北京 100190)
1 前 言
摆动地球敏感器以其优良的性能在地球同步轨道三轴稳定卫星上有很广泛的应用。这种地球敏感器有4个探测器,正常运行时在一定的高度范围内利用4个探测器可以测量出卫星的滚动和俯仰姿态。实际上4个探测器有1个是冗余的,只要有3个探测器能正常工作,即可利用这3个探测器的输出测量出滚动和俯仰姿态,这样当太阳光线干扰地球敏感器时,可通过交替禁止4个探测器中的1个来测量卫星姿态,在1个探测器受扰时仍可测量姿态。
如果地球敏感器1个探测器故障,则在太阳干扰季节会发生需要禁止2个探测器的情况。在以往的卫星应用上没有使用过只有2个探测器输出进行姿态确定的应用。本文结合地球敏感器测量的工作原理给出利用任意2个探测器输出进行姿态确定及控制的实际应用情况,并进行了数学仿真。
2 摆动地球敏感器工作原理
低轨道卫星地球视半径大,普遍应用圆锥扫描式地球敏感器,其探测器扫描整个圆锥,半锥角为55°。而摆动地球敏感器有4个探测器1、2、3、4,探测器1、3扫描线在一个圆锥上,2、4的在另一个圆锥上,每个探测器分别扫描圆锥的一部分,宽扫时每个探测器扫描22°,窄扫时每个探测器扫描11°。按照目前地球敏感器在卫星上的安装方法,定义地球敏感器本体坐标系与卫星本体坐标系重合,探测器1、3扫描圆锥的轴线为卫星本体-y轴,探测器2、4扫描圆锥的轴线为+y轴,半锥角均为83.84°。
从上述描述可以看出地球敏感器扫描均为圆锥扫描,其测量量为一个二面角,如图1所示,弧CD为探测器4的扫描范围,设探测器扫描中心线OA与y(-y)轴形成面Ⅰ,扫入地球线OB与y(-y)轴形成面Ⅱ,探测器测量的二面角为面Ⅰ与面Ⅱ的夹角Δ。

图1 摆动地球敏感器探测器测量示意图
4个探测器测量4个二面角,每个二面角均与地心矢量在本体坐标系中的投影有确定性关系。小角度情况下,通过3个或4个探测器测量均可以线性地测出地心矢量在本体坐标系中的投影。因此地球敏感器测量的本质是测量地心矢量在地球敏感器本体坐标系(与卫星本体坐标系一致)中的分量。通常说地球敏感器测量的是滚动和俯仰角是不确切的,滚动和俯仰角是欧拉角,该角与转序有关,采用不同的转序所得的结果也不同。在欧拉角为小角度情况下,近似与转序无关。平常认为地球敏感器测量的是滚动和俯仰角,是为了直观理解,在应用中也有重要意义,但在分析问题时必须根据其物理本质来分析,才能在任意姿态情况下得出正确的结论。
3 利用2个探测器输出的姿态确定算法
目前在轨航天器应用的地球敏感器,其测量输出为32位的数据,其中包含滚动和俯仰姿态信息,在有3个以上探测器的测量信息时,输出的是滚动和俯仰角,在只有2个探测器测量时,输出的是该2个探测器的二面角信息。我们的目的是利用该2个二面角计算滚动和俯仰角。表1 列出一些有关物理量的定义[1]。

图2 摆动式地球敏感器测量几何

表1 符号定义及物理意义
利用图2所示的测量几何可进行以下计算:
为分析方便,不妨设地心矢量在本体+x轴一侧(在-x轴一侧同理可以推导出相应结果)
(1)
cos(k)=(cosρS-cosαcosα1)/(sinαsinα1)
(2)
当滚动角φ、俯仰角θ为小角度时,对于探测器2、4,α2≈-θ,α1≈90°-φ。对于探测器1、3,α2≈-θ,α1≈90°+φ。
a.探测器2、4的输出
根据测量几何,能够推导出探测器2、4的输出
Δ2=-β-δ+k
(3)
Δ4=+β-δ+k
(4)
在小角度情况下:由式(1) 可知
δ≈-θ
(5)
由式(2) 可知
k=arccos(cosρS/sinα-φcotα)
(6)
把式(6)在φ=0附近展开得到
k= arccos(cosρS/sinα)+
(7)
同时令A= arccos(cosρS/sinα),当为地球同步高度时,A=β=6.2°
式(7)变为
k=A+φ
(8)
将式(5)、(8)代入式(3)、(4)得到探测器2、4的输出
Δ2=-β+θ+A+φ
(9)
Δ4= +β-δ-A-φ
(10)
b.探测器1、3的输出
推导过程同探测器2、4,探测器1、3的输出为
Δ1=-β+θ+A-φ
(11)
Δ3= +β-δ-A+φ
(12)
c.利用2个探测器输出的姿态确定算法
数字式地球敏感器在禁止2个探测器工作时,其输出格式与原来格式相同,但其中的滚动、俯仰姿态输出为正在工作的2个探测器所测量的二面角,具体格式如表2所示。
在禁止2个探测器工作时,根据地球敏感器输出和公式(9)、(10)、(11)、(12)可以进行姿态计算,如表2所示。

表2 禁止2个探测器后地球敏感器的输出及姿态计算情况
上表中,当卫星运行在同步高度时A=β=6.2°,若卫星高度发生变化,则A≠β=6.2°。
从上面的计算可以知道,探测器1、4测量组合及2、3组合不能分离滚动和俯仰姿态,其余任意2个探测器测量组合均可计算出滚动和俯仰姿态。考虑到2个探测器组合主要是在只有3个探测器可用而又有太阳干扰其中一个时应用,一个探测器受太阳干扰最长时间不超过90 min,此时卫星工作在正常模式,如果是偏置动量卫星,滚动角度不会太大,可认为这2个探测器的测量变化就是由于俯仰角变化引起的。因此把滚动角与俯仰角之和或差作为控制量来控制,只要滚动角度变化不大,卫星控制是稳定的,仿真结果也表明这样做是合理的。这样对于只有3个探测器输出时,在春分、秋分前后太阳干扰地球敏感器季节地球敏感器仍然可以正常使用。这就大幅度扩展了地球敏感器的可用性,对于故障重构具有重要意义。
4 仿真计算
首先由地球敏感器的测量模型,根据本体对轨道的方向余弦阵构造出地球敏感器4个探测器的输出,该模型在北京控制工程研究所开发的同步卫星模拟器[2]中已成功应用。仿真计算分2部分,一是给定滚动和俯仰姿态的情况下,禁止2个探测器工作,通过电激励信号驱动真实地球敏感器线路,根据地球敏感器实际输出结果,计算出除1、4及2、3组合外的其它组合测量输出及姿态计算结果,如表3所示;同时根据地球敏感器的测量模型,构造其输出,仿真计算在给定的多种滚动和俯仰姿态组合的情况下,禁止2个探测器工作时的姿态确定结果,给出除1、4及2、3组合外的其它组合测量输出及姿态计算结果(如表4所示),可以看出利用真实地球敏感器的测试结果与利用模型的仿真结果是一致的。二是各种测量组合下闭路控制仿真计算,包括太阳干扰时使用1、4或2、3探测器测量组合的控制仿真。仿真结果表明控制效果良好。

表3 同步轨道给定姿态下利用真实地球敏感器2个探测器输出姿态确定结果(单位/°)
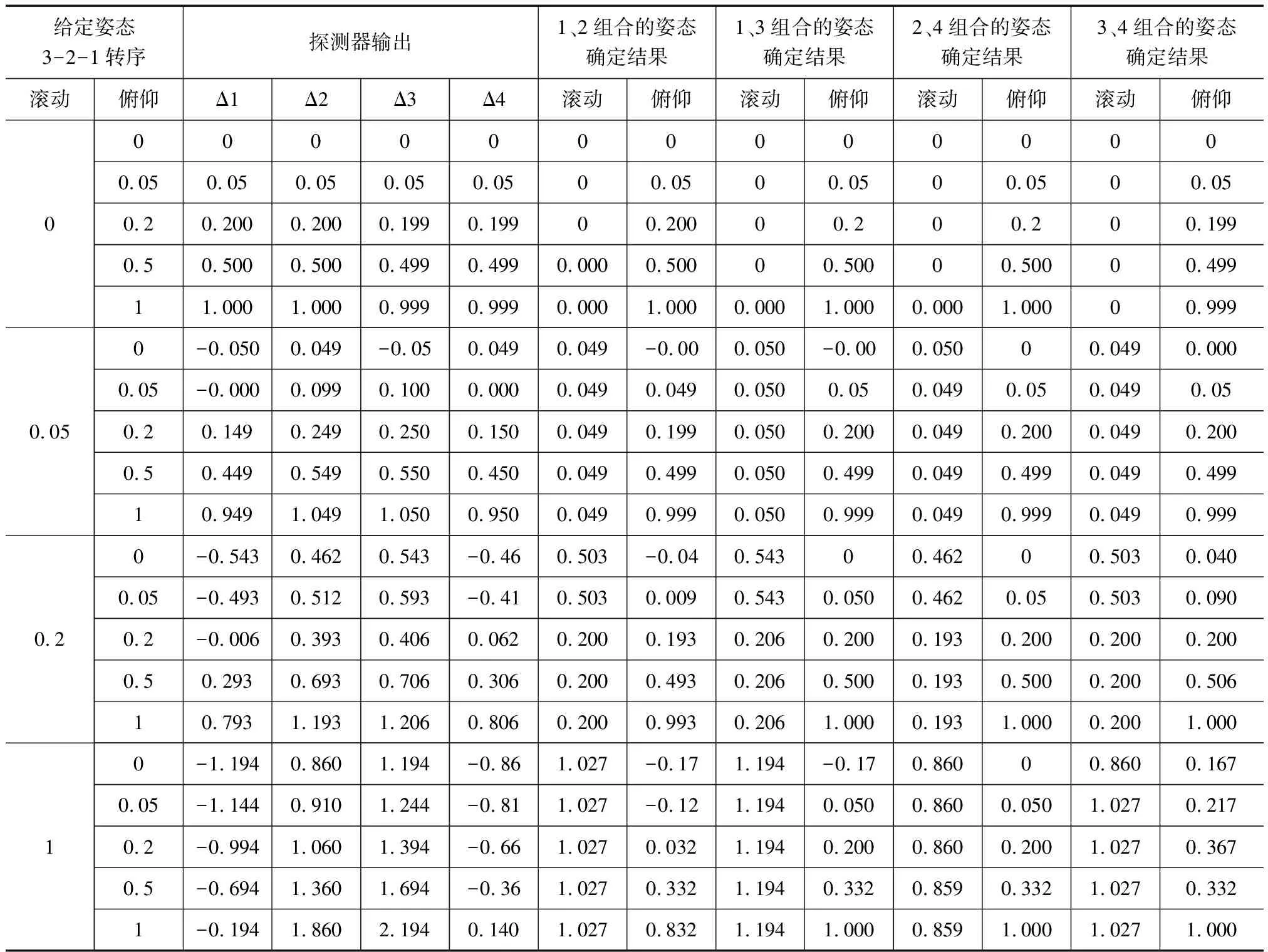
表4 同步轨道给定姿态下利用地球敏感器模型两个探测器输出姿态确定结果(单位/°)
在地球指向模式下利用探测器组合1、2,1、3,2、4及3、4测量进行姿态确定和控制的闭路仿真,结果与利用3个或4个探测器的情况区别不明显,说明完全可以利用这几种组合的2个探测器进行姿态确定和控制,在此不再给出仿真结果。
图3、4的仿真曲线为利用不能分离出滚动、俯仰姿态的1、4或2、3探测器组合的测量控制仿真结果,初始条件为:滚动姿态0°,角速度0.002(°)/s;俯仰姿态0°,角速度0.0005(°)/s;偏航姿态0.15°,角速度0.0005(°)/s;仿真起始为过渡模式,允许自动转入正常模式,俯仰方向具有-93N·m·s的偏置角动量。利用尼日利亚一号卫星模拟器进行仿真计算,在1 500 s左右,发送禁止探测器2、3或1、4的指令,只控俯仰,不控滚动,得到两条曲线。仿真时间2h以上,姿态不发散,滚动和偏航仅在一定范围内章动,俯仰姿态根据不同的探测器组合,与滚动姿态相同或相反,具有较强的实用价值。

图3 正常模式探测器2、3禁止,利用探测器1、4测量进行控制的结果

图4 正常模式探测器1、4禁止,利用探测器2、3测量进行控制的结果
5 总 结
本文揭示了摆动式地球敏感器的测量本质,并给出了利用2个探测器进行姿态计算的方法和结果。利用摆动式地球敏感器的两个探测器进行姿态计算可以大大扩展地球敏感器的使用范围,对于故障重构具有重要意义,特别是对偏置动量卫星在同步轨道稳定运行段的姿态确定意义更大。对于两万公里以下及四万公里以上的卫星是否可以应用还有待进一步研究。

