故事与思想方法

孟　坤

在许多故事中，蕴涵着深邃的数学思想方法.如果我们多读些故事，则能启迪我们的思维，获得数学的灵感，提高我们的数学素养.

一、司马光砸缸与逆向思维

司马光砸缸是同学们比较熟悉的一个故事.人掉进水里，按习惯性思维，是把人从水中捞出来，而司马光不能做到从水中捞人，于是他寻求变异，从另一个角度思考：让水离开人！因此他果断地用石头砸缸放水，救了小伙伴.从此，司马光砸缸救人的事迹被传为佳话，流传千古.司马光砸缸救人，从思维的角度讲，他是成功地运用了逆向思维.

在解决问题的过程中，对已知信息可以多方向、多角度地思考，不局限于原来的方法，可用逆向思维的办法解决问题.

例1有一天刘明和李亮驾车去动物园，在路上，他们有一段对话.

刘明：“看前面的那辆大卡车，开得真快，但是我们可以赶上它.现估计它以每小时65千米的速度匀速前进，而我以每小时80千米的速度匀速追赶.假设我们现在正好在它后面1.5千米，如果我们不去超他的车的话，那么就肯定会同它相撞.李亮，请你告诉我，在相撞前一分钟，我们与它相距多远？”

李亮：“那很简单，在相撞前一分钟，我们与它相距250米.”

李亮答对了吗？他为什么答得这么快？他是怎么算的？

解析：这个问题若考虑用列方程或者更加“高级”的方法，那就搞复杂了.而且李亮也不能马上算出答案.他是怎么算出来的？实际上他是从时间上倒过来考虑，马上得出答案的.由于卡车以每小时65千米匀速行驶，小车以每小时80千米匀速前进，所以每小时小车比卡车多走15千米，即每分钟小车比卡车多走250米.因此，在相撞前一分钟，小车与卡车相距250米.

刘明提出问题时，小车落后于卡车1.5千米，其实此条件对解这个问题是多余的，不管这两辆车之间的初始距离是多少，该题的答案只有一个！这种思考方法很值得借鉴.

二、神童量水与分类思想

有一天，一位国王在后花园里散步，忽然指着水池问身边的大臣：“池中有几桶水？”大臣们都被这古怪的问题问住了，谁都答不上来.这时，有位大臣奏道：“城东有个小孩，人称神童，要不叫他来试一试？”于是国王下令宣小孩进宫.小孩听了国王的问题，眼睛眨巴了两下，随口答道：“如果桶和水池一样大，就是一桶水；如果桶比水池小一半，就是两桶水；如果桶的大小是水池的三分之一，就是三桶水；如果……”没等小孩说完国王便连连赞道：“答得好，答得妙！真是聪明过人.”

细细品味上述故事，小孩的确答得妙，妙在一个众人认为不易回答的问题，小孩能分情况考虑巧妙地答出，他这种思考问题的方法，实质上就是分类讨论的数学思想方法.

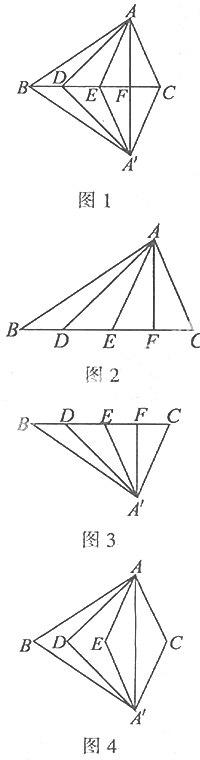
例2数一数图1中有几个三角形.

解析：我们按以下步骤分步进行：（1）先看图形的上半部分（如图2）.如果把4个小三角形中的每一个都看做“基本单位”，那么每2个相邻的基本单位又可构成三角形，这样的三角形有3个，每3个相邻的基本单位可构成2个三角形，4个基本单位构成1个大三角形.于是图形的上半部分共有三角形：4+3+2+1=10（个）.（2）如图3，同理图形的下半部分也有10个三角形.（3）再看整个图形，将中间的线段去掉，如图4，这里有4个三角形，都以AA′为公共边.因此，图1中共有三角形：10+10+4=24（个）.

利用分类思想数图形的个数，可以使复杂问题简单化，解决问题的过程更加清晰、有条理.分类时，要做到既不能重复，也不能遗漏某些部分，当然同一问题也可能有多种分类的方法.

三、“大敦穴”的发现与归纳法

有一个樵夫经常犯头疼病，但找不到治疗的办法.有一次，这个樵夫上山去砍柴，无意中碰破了脚的大拇指，出了一点血，但这时他却感到头部不疼了，当时他也没有在意.后来，他的头疼病复发，在砍柴时又偶然碰破了上次碰破的地方，这时他的头疼又好了，这次却引起了他的注意：奇怪，为什么碰了这个部位，我的头疼就好了呢？于是便记住了这个部位.以后，每当他犯头疼病的时候，就有意识地去刺破这个部位，结果头疼马上就好了.这个樵夫所碰的部位，就是现在人体穴位中的大敦穴，它在脚的大拇指的指甲的外侧根部.这个樵夫发现大敦穴的过程，就是采用了“归纳法”的思想.

归纳法就是从特殊的具体的认识推断出一般的抽象的认识的一种思维方法.它是科学发现的一种常用的有效的思维方法.

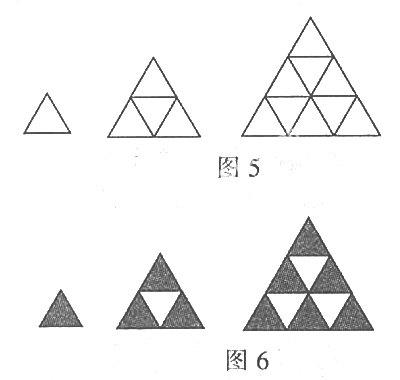
例3用长度相等的小木棒按图5所示的方式搭三角形，按照这样的规律搭下去，搭建第10个图形需要（）根小木棒.

解析：如图6，从第1个图形到第10个图形，在每个图形的内部，由独立的三根小木棒搭建而成的小三角形的个数分别为1，（1+2），（1+2+3），（1+2+3+4），…，（1+2+…+10），所以第10个图形需要小木棒的根数为（1+2+…+10）×3=165.

解决本题的关键是通过观察、分析、比较，依据图形找出变化规律.