《轴对称》单元测试题
何萧萧
学数学,绝不会有过分的努力.
——卡拉吉•奥多里(20世纪希腊数学家)
一、填空题(每小题3分,共30分)
1. 在A、E、F、G、H、K、M、N、O、R十个英文字母中,可看成是轴对称图形的有__.
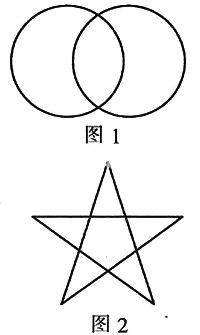
2. 图1和图2都是轴对称图形,图1有__条对称轴,图2有__条对称轴.
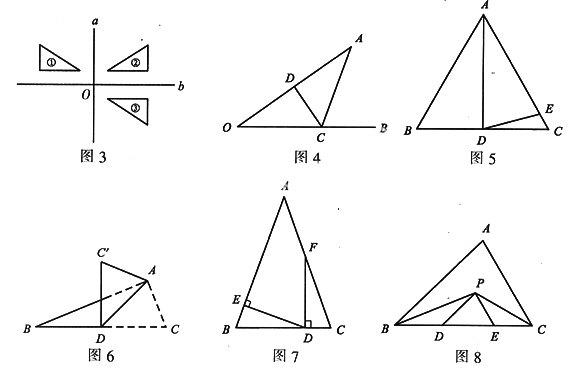
3. 如图3,已知直线a⊥b,交点为O,则图形①与图形__轴对称.
4. 等腰三角形中有一个角为52°,则它腰上的高与底边的夹角为__.
5. 等腰三角形一条边的长是另一条边的长的2倍.若此等腰三角形的周长为40,则腰长为__.
6. 如图4,已知∠O=35°,CD为OA的垂直平分线,则∠ACB=__.
7. 如图5,若在△ABC中,AB=AC,∠BAD=30°,BD=CD,AE=AD,则∠EDC=__.
8. 如图6,AD是△ABC的中线,∠ADC=45°.将△ADC沿AD翻折,点C落在点C′处,则BD与C′D的大小关系是__,位置关系是__.
9. 如图7,在△ABC中,AB=AC,DE⊥AB,DF⊥BC,∠AFD=160°,则∠EDF=__.
10. 如图8,在△ABC中,BC=16 cm,BP、CP分别平分∠ABC和∠ACB,且PD∥AB,PE∥AC,则△PDE的周长为__.
二、选择题(每小题3分,共30分)
11. 妈妈新买的一件衣服上有一个标签,上面有如下几个图形,分别表示这件衣服可干洗,应低温烫,不可漂白和悬挂晾干.这几个图形中是轴对称图形的是().

12. 下列图形中,不是轴对称图形的是().
A. 有两个内角相等的三角形
B. 有一个内角是45°的直角三角形
C. 有一个内角是30°的直角三角形
D. 有两个内角分别是30°和120°的三角形
13. 如图9,将△ABC变换到△A′B′C′的位置,下列说法正确的是().
A. △ABC与△A′B′C′是关于x轴对称的
B. △ABC与△A′B′C′是关于y轴对称的
C. △ABC与△A′B′C′是关于点O对称的
D. △ABC与△A′B′C′既关于x轴对称,又关于y轴对称
14. 已知在直线l同旁有两点A、B.在l上求一点P,使PA+PB最小,则P点的作法为().
A. 作A关于l的对称点A′,连接A′B交l于P
B. 作A关于l的对称点A′,连接AA′交l于P
C. 作AB的延长线与l交于P
D. 以上都不对

15. 平面直角坐标系内点A(-1,2)和点B(-1,6)的对称轴是().
A. x轴B. y轴C. 直线y=4D. 直线x=-1
16. 如图10,在△ABC中,∠C=90°,∠A=30°.在直线BC或AC上取一点P,使得△PAB是等腰三角形,则符合条件的点P有().
A. 2个 B. 4个C. 5个 D. 6个
17. 如图11,已知AE⊥AB,BC⊥AB,AB=AE=2BC,D为AB的中点.有以下结论:①DE=AC;②DE⊥AC;③∠CAB=30°;④∠EAF=∠ADE.其中正确的结论有().
A. 1个 B. 2个 C. 3个D. 4个
18. 如图12,△ABC中,D、E分别是AC、AB上的点,BD与CE相交于点O.给出下列四个条件:①∠EBO=∠DCO;②∠BEO=∠CDO;③BE=CD;④OB=OC.选其中两个条件为一组作为题设,则可推出△ABC是等腰三角形的有().
A. 1组 B. 2组 C. 3组 D. 4组
19. 如图13,△ABC中,∠ABC与∠ACB的平分线交于点F.过点F作DE∥BC交AB于点D,交AC于点E.有下列结论:①△BDF和△CEF都是等腰三角形;②DE=BD+CE;③△ADE的周长等于AB与AC的长度之和;④BF=CF.其中正确的有().
A. ①②③ B. ①②③④
C. ①② D. ①
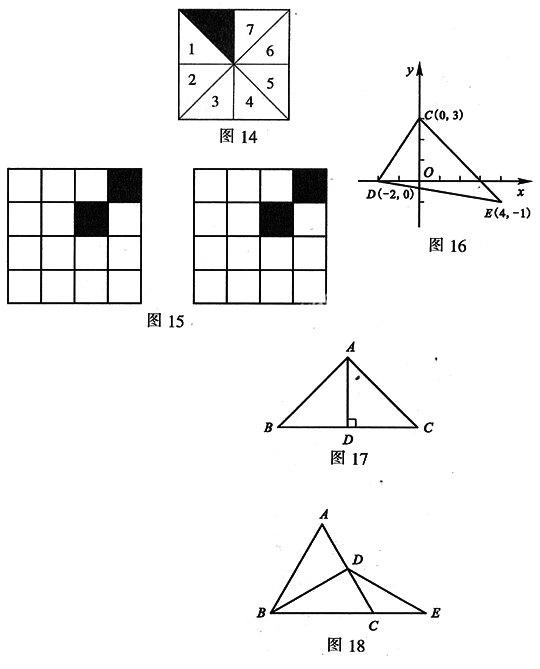
20. 图14中,与阴影三角形轴对称的三角形共有().
A.2个B.3个C.4个D.5个
三、解答题
21. (6分)由16个相同的小正方形拼成正方形网格,现将其中的两个小正方形涂黑(如图15).请你用两种不同的方法分别在图15中再将两个空白的小正方形涂黑,使其成为轴对称图形.
22. (6分)如图16,利用关于坐标轴对称的点的坐标的特点,分别作出△CDE关于x轴和y轴对称的图形.
23. (8分)小玉同学在学习了等腰三角形后,做了一道题,过程如下.
已知△ABC是等腰三角形,BC边上的高AD恰好等于BC边长的一半,求∠BAC.
解:如图17.

∵AD⊥BC,AD=1/2BC=BD=CD,
∴∠BAD=∠B=∠C=∠CAD=45°.
∴∠BAC=90°.
小玉的解答正确吗?若不正确,请给出正确的解答.
24. (8分)如图18所示,△ABC为等边三角形,BD是中线.延长BC到点E,使CE=CD.不添加辅助线,请你写出尽可能多的结论(至少4个).图中有等腰三角形吗?如果有,试证明其中的一个(△ABC除外).
25. (10分)如图19,E、F分别是等边△ABC的边AB、AC上的点,如果AE=CF,那么BE与AF、BF与CE是否相等?若BF与CE交于点P,当点E、F分别在边AB、AC上移动时(不考虑端点),且AE=CF,∠BPE的大小是否随之变化?
26. (10分)如图20,梯形纸片ABCD中,AD∥BC,∠B=90°.若沿AC折叠,则点B恰好落在CD的中点E上.求证:△ACD是等边三角形.
27. (12分)如图21,点C为线段AB上一点,△ACM和△CBN都是等边三角形.AN交MC于点E,BM交CN于点F.
(1)求证:△CEF为等边三角形.
(2)将△ACM绕点C按逆时针方向旋转90°,其他条件不变,在图22中补出符合要求的图形,并判断(1)中的结论是否仍然成立(不要求证明).
- 中学生数理化·八年级数学人教版的其它文章
- 如何对待难题
- 把书本与笔记合二为一
- 全等三角形开放型问题评析
- 折叠与轴对称
- 聚焦等腰三角形中的探索型问题
- 杯子里的互质数

