对称给我们带来的数学美
作者简介:王继延,理学硕士. 曾执教高中十余年,并任中学校长. 现为华东师范大学数学系教授,国家数学课程标准核心组成员,全国初中数学实验教科书(华东师大版)常务副主编,教育部基础司项目“全国初中毕业、升学考试评价”数学学科负责人. 作为主编或主要人员参与编写或翻译多本数学教育专业著作与教材,如《全国初中数学实验教科书》《基础教育新课程师资培训指导(初中数学)》《数学教与学研究手册》《数学教学理论选讲》《数学物理方程》《文科数学-数学思想和方法》与《高中数学选修读本》等书,在《人民教育》《数学学报》《高等数学研究》《生态学报》《数学教学》等杂志上发表多篇文章.
同学们,对称美吗?请听王教授给我们一一解析对称的数学美吧.
你看,图1是某些名胜古迹的一些照片.

你发现了吗?这三张照片中的北京天安门、河南开封府与印度泰姬陵的图片都是轴对称图形,那个印度泰姬陵与水中的倒影还恰好成轴对称呢!生活中也有不少那样美的图形,如图2的蝴蝶与螃蟹的照片.
那么这些轴对称图形给我们带来什么信息呢?
让我们从最简单的轴对称图形说起吧.你看,将一条直线段绕着它的中点对折,两半一定重合.线段就是一种简单的轴对称图形.折痕,即对称轴,就是线段的垂直平分线.通过类似的操作实验,你还可以知道角是另一种简单的轴对称图形,折痕,即对称轴,就是角平分线所在的直线.由这些操作,我们还可得到垂直平分线与角平分线的一些性质.
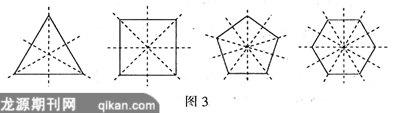
那么一个轴对称图形的对称轴是否只有一条呢?当然不是!你看图3的一些图形,有的有三条,有的则更多.
现在请你观察一下,如下的一些汉字中,哪些是轴对称图形?如果是,那么它们各有几条对称轴?
上下目天田土吕林显王
经过观察和实验操作,我们可以发现轴对称图形的基本性质是:关于对称轴对应的线段相等,对应的角也相等,连接对应点的线段的垂直平分线就是这一轴对称图形的对称轴.这就告诉我们,经过轴对称这一图形的变换,图形的形状与大小都没有发生变化.
你看!图4是一个飞机模型的一半,请你画出整个飞机模型.

我们已经看到等边三角形是一个轴对称图形,它有三条对称轴.那么如果只有两条边相等,也就是等腰三角形,它是否是轴对称图形呢?做个实验,猜测一下.画一个等腰三角形,剪下,将其对折(如图5),发现了什么?每位同学剪的等腰三角形有大有小,但有一点应该是完全一样的:对折后的两半完全重合!
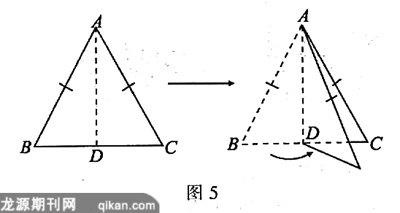
那就是说等腰三角形是一个轴对称图形,那个折痕就是它的对称轴.据此,你还能发现等腰三角形的性质:两个底角相等,底边上的中线、高和顶角平分线互相重合(三线合一).当然还有反过来的结论:两个内角相等的三角形是等腰三角形.这些可是十分重要的结论,需要我们理解记住,以后很多地方都会用到呢.
图形的变换,我们今天说了一个:轴对称.以后还会学习和研究另外几个,有如同轴对称那样使图形的形状与大小都不发生变化的平移与旋转,还有保持图形形状不变,大小可能发生变化的相似变换.这些变换都是我们研究几何问题的重要工具.
好了,今天就说到这里啦,还是让我们一起多想想吧,生活周围到处充满了轴对称给我们带来的数学美!
练习题:
1.如图6,在长方形台球桌面上有两个球M、N,怎样击打球M,可使其撞击一桌边缘反弹后,正好击中球N?(读者还可考虑:若击打球M,使其连续撞击两条或三条桌边缘反弹后,正好击中球N.那么该如何击打?)
2.图7画着的箭头是一个上下对称的轴对称图形,现在只知道其中一个角的大小和两条线段的关系.要求你剪两刀,把它剪成三块,再拼成一个正方形.想想看,该怎样剪.
3.如图8,一辆汽车在直线形的公路AB上由A处向B处行驶.M、N分别是位于公路两侧的村庄.
(1)当汽车从A出发向B行驶时,在公路的哪一段路上距离两村庄M、N都越来越近?在哪一段路上距离村庄N越来越近,而离村庄M却越来越远?何处距离村庄N最近?
(2)在公路上是否存在这样一点H,使汽车行驶到该点位置时,恰好与两村庄M、N的距离相等?如果存在,请画出这一点;如果不存在,请简要说明理由.
参考答案:
1.作点N关于桌边的对称点N′,连接MN′,与桌边交于点C.则沿着MC方向击球,即可达到目的.
2.如图9.
3.(1)分别过点M、N作直线AB的垂线,设垂足为E、F.显然当汽车在AE上行驶时,距离两村庄M、N都越来越近;而当汽车在EF上行驶时,距离村庄N越来越近,而离村庄M却越来越远;当汽车行驶到点F处时,距离村庄N最近.
(2)存在这样的点H.作线段MN的垂直平分线,与AB的交点即是点H.

