巧设元 妙解题

朱元生

一元一次方程在数学问题中的应用非常广泛，只要巧设元，总能将问题轻松解决.

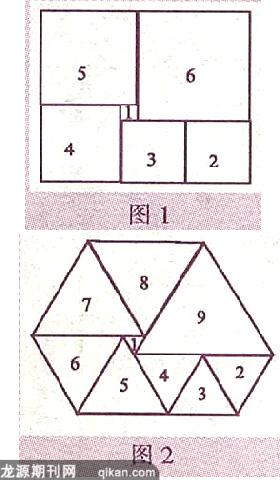
例1图1是由六个正方形拼成的长方形，已知中间的小正方形的边长为1，试求长方形的面积.

解析：给六个正方形分别标上1、2、3、4、5、6.

设正方形2的边长为x，则正方形3的边长也为x，正方形4的边长为（x+1），正方形5的边长为（x+2），正方形6的边长为（x+3）.

根据长方形的对边相等，可得方程:

x+x+（x+1）=（x+2）+（x+3）.

解得x=4.

从而得到长方形的长为3x+1=13，宽为2x+3=11.

所以长方形的面积为13×11=143.

例2图2是由9个等边三角形拼成的六边形，若已知中间的小等边三角形的边长为a，则六边形的周长是.

解析：给9个等边三角形分别标上1、2、3、4、5、6、7、8、9，设等边三角形2的边长为x，则等边三角形3、4的边长也为x，等边三角形5、6的边长为（x+a），等边三角形7、8的边长为（x+2a），等边三角形9的边长为（x+3a）.

从图中可以看出，等边三角形9的边长等于等边三角形2、4的边长之和，可得方程：x+3a=2x.解得x=3a.

所以六边形的周长为x+x+（x+a）+（x+a）+（x+2a）+（x+2a）+（x+3a）=7x+9a=7×3a+9a=30a.

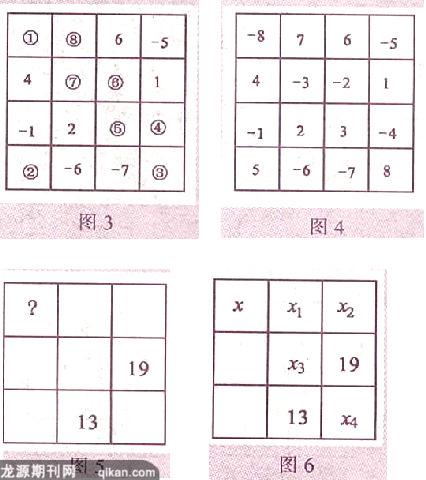
例3将-1～-8和1～8这16个整数填入4×4的正方形表格中，使得每行、每列、每条对角线上四个数之和都相等，如图3所示.其中有8个标有序号（带圆圈的数字）的小方格中填的数被一个顽皮的小朋友擦掉了，请你将这擦掉的8个数恢复出来.

解析：所填表中每行、每列、每条对角线上的四数之和都相等，设这个和为S，则4S=（-1）+（-2）+…+（-8）+1+2+…+8=0，得S=0.

故所填表格中每行、每列、每条对角线上的四数之和都为0.

设方格①中的数为x，则方格②中的数为-3-x；方格③中的数为13-（-3-x）=16+x；方格④中的数为-12-x；方格⑤中的数为11+x；方格⑥中的数为-10-x；方格⑦中的数为5+x；方格⑧中的数为-1-x.

由对角线上的①、⑦、⑤、③四数之和为0，得x+（5+x）+（11+x）+（16+x）=0.得到x=-8.

于是可以依次算出被擦掉的各数，恢复后如图4所示.

练习题在图5中有9个方格，要求在每个方格内填入不同的数，使得每行、每列、每条对角线上的三个数之和都相等，试问:图中左上角问号处的数是多少？

答案与提示：虽然要求的只是左上角的数，但是题目中的条件还与其他的数有关，因此需恰当地增设不同的字母来表示数，以便充分运用已知条件.

如图6，设相应方格中的数分别为x1，x2，x3和x4，问号处填入的数为x，由已知条件得：

x+x1+x2=x+x3+x4=x1+x3+13=x2+19+x4.

由前两个式子之和等于后两个式子之和，得到：

2x+x1+x2+x3+x4=13+19+x1+x2+x3+x4.

所以2x=13+19.解得x=16，即图中左上角问号处的数为16.