舰船水消防系统生命力评估中信息融合理论的运用

1 引 言

舰船消防系统是保障舰船生命力的重要系统，排水系统、灭火系统是其重要组成部分，而这些系统在舰船上从舰首至舰尾,从底舱至舰桥广泛分布，系统间元件功能相互关系十分复杂，其损伤的因素很多且具有不确定性[1]。要真正较高精度地解决这样一个复杂系统在各种攻击情况下的生命力问题利用传统经典的方法是难以完成的。

Dempster-Shafer(简称D-S)证据组合理论在信息融合中获得了广泛的应用，它比传统概率论更好地把握了问题的未知性和不确定性。但是，D-S证据组合理论本身也存在不少问题,如证据组合引起的焦元爆炸,组合条件十分严格等。对于不同来源的证据具有不同的可靠性和权威性，这一普遍存在的现象却很少在证据理论中体现出来。粗集理论能有效地分析和处理各种不完备信息，并从中发现隐含的知识，揭示潜在的规律，为处理不完备信息提供了一种更符合人类认知的知识理论。针对上述情况,根据粗集理论和证据理论的基本关系,提出了一种基于粗集理论的加权证据理论多源信息融合方法，并把该方法应用到舰船水消防系统的生命力评估中，取得了良好效果。

2 证据理论的应用

D-S证据组合理论是讨论一个辨识框架U,它是关于命题的相互独立的可能答案或假设的一个有限集合。按传统方法可以把U的幂集表示为2U，它是U的所有子集的集合。D-S证据理论对这个辨识框架进行运算,并提供计算幂集元素的逻辑,然后使用这些计算结果完成高和低不确定性的计算工作[2]。

给定一识别框U，m:2U→[0,1]是U上的可信度分配，定义函数：

Bel:2U→[0,1]

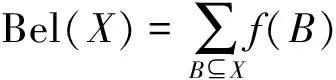
(1)

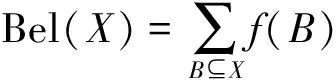
Bel(φ)=0, Bel(U)=1

(2)

(3)

称[Bel(A),pl(A)为A的信任区间，信任区间刻划了对A的信任程度的上下界限。

又假设Bel1,Bel2,…，Belt为论域U上t个独立证据的信任函数，其相应的基本概率分配函数(可信度分配函数)分别为：f1,f2, …,ft，相应的焦点元素分别为：

A11,A12,…,A1K1，A21，A22，…,A2K2，…,At1,At2,…AtK1

(4)

若K1<1，则融合后的可信度分配为：

(5)

由上述定义给出的D-S组合规则，满足交换率和结合率，因此对于多个证据信息融合，可采用D-S规则进行两两组合，且融合的结果和各组证据信息融合次序无关[3]。

3 基于粗糙集理论的权重发现

粗糙集理论的出发点是,根据目前已有的对给定问题的知识将问题的论域进行划分,然后对划分后的每一个组成部分确定其对某一概念的支持程度:即肯定支持此概念、肯定不支持此概念和可能支持此概念。在粗糙集理论中,以上三种情况分别用三个近似集合来表示为正域、负域和边界[4]。

(6)

对于决策系统S=(U,C∪D)，C为条件属性集合，D为决策属性集合。B⊂C，定义B相对于D的正域为：POSB(D)={B|X∈U/IND(D)}，其中,U/IND(D)为D对U划分所得到的等价类集合。POSB(D)实际上是那些可以根据属性集合B准确地被分入由属性D所确定的分类元素的集合。为此，重要性可以用以下2个公式进行判断，即

rC(D)=card(posC(D))/card(U)

(7)

去掉属性a后,

rC-{a}(D)=card(posC-{a}(D))/card(U)

(8)

式中， card(·)表示集合的基数，当从条件属性集C中去掉属性a后再进行分类时，分类U/D的正域改变可以表示为属性a的重要程度，可表示为：

ra=rC(D)-rC-{a}(D)

(9)

对于属性集中各个属性权重的确定，可以将所有属性的重要程度进行规范化处理。

(10)

4 证据加权调整方法

证据权是该条证据在所有证据中重要性的度量指标，体现了对最终合成结果的贡献程度。若对整个证据只有一个1-α的确信度，在对证据打折扣的情况下，信任函数和基本概率赋值的变化可以通过下面的定理给出有关结论[5]：

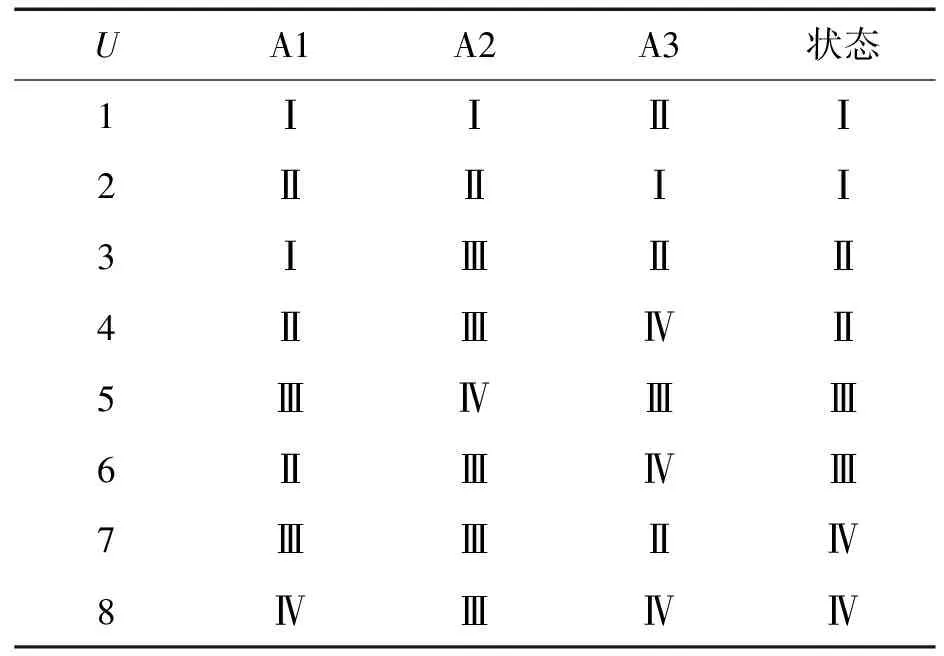
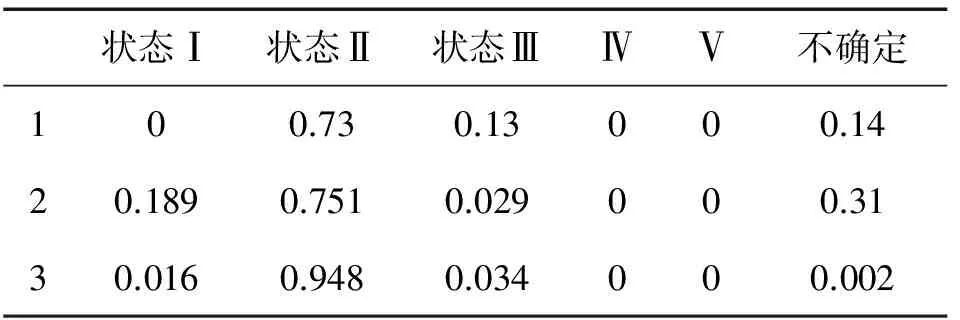
定理1：设BEL:2U→[0,1]是一个信任函数，0

BELa(U)=1

BELa(A)=(1-a)BEL(A),∀A⊂U&A≠Φ

(11)

则BELa是一个信任函数。

定理2:设BELa为定理所规定的信任函数，则其对应的基本概率分配ma:2U→[0,1]满足：

ma(U)=(1-a)m(U)+a

ma(A)=(1-a)m(A),∀A⊂U&A≠Φ

(12)

为此，若运用粗集理论进行D-S证据推理的加权修正，可以按照如下步骤进行：

1) 根据具体系统，确定初始决策表中的例子，可以运用最近根据证据理论得到的结论，假设系统输入信息源为M个，则决策表中前M列为条件属性，最后一列为决策属性。

2) 将输入样本信息离散化，并形成决策表。按照上述粗集理论计算各证据的基本概率权。

3) 设识别框架为Θ={A1,A2,…,At}，A1,A2,…,At为识别框架的t个焦元，有k条证据支持命题。第i条证据为首要证据，其证据权qi，第j条证据权qj，其相对于首要证据的信任度βj=qj/qi。

4) 以βj视为这个证据的信任度，依据证据权对第j条证据的基本可信度进行转换，经过转换后的基本可信度分配为m′(Aj)=βjm(Aj)。

5) 应用D-S组和规则进行证据合成，得到最终的结果。

6) 对新样本进行加权证据融合计算。

7) 决策输出。

5 实例分析

对舰船水消防系统生命力进行评估常用的证据有：一次命中消防栓失效概率A1、消防泵功率损失指标A2和水消防系统不保证供电概率A3。这3种参量对舰船水消防系统生命力的评估是不全面的、不完全的。为此，这3种信源对水消防系统生命力最终评价的权重是不相同的，而且各自的权重大小受到诸多因素的影响。运用粗集理论对这3种参量进行权重判断，结合D-S证据理论，得到状态评估的最终结论。表1是一个经过简化和离散化处理得到的舰船水消防系统生命力评估实例表(以A1,A2,A3表示3种信源的评估结果,以Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ表示水消防系统生命力评估结论，分别表示近乎完好、轻度损伤、中等程度损伤、严重损伤和完全失效)。

表1 舰船水消防系统生命力评估实例表

表1中U表示实例集， 状态列表示的是3种指标综合评价的结论。 对表1进行计算， 可得：

posC(D)={1,2,3,4,5,6,7,8},rc(D)=1

posC-{a}(D)={1,2,5},rc-{a}(D)=3/8，

r{a}=5/8

posC-{b}(D)={2,5,7,8},

rc-{b}(D)=4/8,r{b}=4/8

posC-{c}(D)={1,2,3,5,7,8},

rc-{c}(D)=6/8,rc=2/8

进行规范化处理后得到各自的权重：

Wa=5/11，Wa=4/11，Wa=2/11。

利用一次命中消防栓失效概率A1、消防泵功率损失指标A2和水消防系统不保证供电概率A3,对水消防系统生命力进行融合评价，建立D-S证据理论的识别框架为舰船水消防系统的5种状态，将3种评价分析结果作为基本概率赋值,各证据不相关。某次评估过程中，由专家通过对3种信源的分析得到如表2所示的可信度表。

表2 可信度表

对不同信源的评估结果进行融合，先求出一次命中消防栓失效概率A1和消防泵功率损失指标A2评估结果融合后的各状态可信度分配；将融合后的结果再与水消防系统不保证供电概率A3判定的结果进行融合,最终求出3种信源参数融合后的各状态可信度分配，结果如表3所示。若在上述融合过程中运用粗集分析得到的证据权进行融合，其结果如表4所示。

从表4可以看出，通过对3个信源的评估结果的融合比较，说明了对证据加权后可以提高融合的精度，采用基于信任函数的决策方法，可以对水消防系统生命力作出评估。 同时可以看出， 每多进行一次融合，水消防系统生命力的评估精度得到了提高。

表3 各步骤融合状态可信度表

表4 经过加权的各步骤融合状态可信度表

6 结 论

本文提出了一种基于粗集理论的加权证据理论多源信息融合方法。该方法将粗集理论与证据理论相结合,通过对成功的融合例子进一步数据挖掘，发现用于融合的各信源不同的重要性，进而确定其各自的权重因子。应该看到,粗集理论采用概念的上、下近似来处理信息，具有客观性，但是所选取的样本数据一定要有普遍性和代表性。如果选取的原始样本数据非常少，且不具有代表性,则会出现随着计算样本的增加,权值也会发生变化。同时对原始定量数据的离散化方法的不同也会影响权值系数的值。

[1] 邱金水，董学江，王树明.舰船损管系统生命力评估[J].海军工程大学学报，2003(4):51-56.

[2] HALL D L, LLINAS J. An introduction to multisensor data fusion[J]. Proceedings of the IEEE, 1997,85(1):6-20.

[3] VICENE T A. A new combining function in evidence theory[J]. International Journal of Intelligence system,1995,5(10):1021-1033.

[4] 曾黄麟.粗集理论及其应用—关于数据推理的新方法[M].重庆:重庆大学出版社,1996.

[5] 何友，王国宏，陆大金,彭应宁.多传感器信息融合及应用[M].北京：电子工业出版社，2000.