海洋平台结构系统弹塑性整体计算的裂纹柱壳新单元

1 引 言

以柱壳为基本构件的结构系统常见于海洋工程等大型复杂结构物中。由于柱壳良好的综合性能，船舶与海洋工程的各种平台大多将其作为主体结构。通常此类平台造价昂贵，平台上载有各种专用设备并有较多的人员在平台上工作，因此一旦发生重大安全事故，将可能造成巨大的生命财产损失，甚至导致海洋环境的严重污染和社会层面上的连锁负面反应；另一方面，海洋平台在服役期间长期处于较为恶劣的环境之中，尽管平台的安全性设计要求非常高，但历史事实表明也未能完全避免灾难性事故的发生。应该说在安全系数较大的前提下，一般意义上的强度或失稳破坏不易发生，但究其原因，一个重要的问题是未充分考虑无法回避的自身的隐伤或服役期间所产生的损伤、破损等因素的影响。由于各种交变疲劳载荷的长期冲击，裂纹损伤是各种损伤中最常见且最危险的一种损伤形式。

另一方面，如何从结构系统的角度判断在裂纹损伤条件下的安全度，正确评估结构系统的残余寿命，科学地制定保护维修方案，有效进行裂纹控制，是精确评估平台安全性的一个重要课题。很明显,只有实现裂纹损伤条件下的结构系统整体分析才能回答上述相关问题，但用现行的传统方法无法得到满意的答案。对于“裂纹”也许会首先想到“断裂力学”；而涉及到结构系统或许会想到“结构力学”，可这两者的关注点差别很大。“断裂力学”可处理线性到非线性，以及脆断到撕裂的问题，但它最终关注的是如何表达裂纹尖端的力学特性，所以,一般而言它着眼于单一孤立构件的“局部”，其方法不能提供与结构系统之间相互影响的关系；而“结构力学”已可对复杂结构系统进行非线性极限分析，但在其“整体”中无法涉及如裂纹这样的损伤，即对局部的地方出现的裂纹损伤的力学特性如何表现显得无能为力。通用的三维有限元方法从原理上似乎可以将上述所谓“整体”和“局部”放在一起求解，但因裂纹尖端奇异性特点，仅对单一裂纹构件和裂纹尖端单元网格的密分数据量就已非常可观，与之相关联的结构系统的其它构件则因此很难再考虑。非常大的建模工作量和数据量使得对海洋工程平台这样复杂的结构系统的求解变得非常困难。由此产生了研究和开发一个具有有限元特点的含裂纹影响的理想化单元的设想。通过一个单元来包含裂纹影响的力学信息，使单元网格划分最大限度地减少，从而实现对复杂结构系统整体的分析评价。

目前国内外尚不存在这样一个完善的单元。由于材料科学的发展，高韧性材料被广泛使用，在外力作用下，裂纹扩展前，其前端附近将出现不能忽略的较大范围的塑性区域，在结构系统整体分析中如何考虑这一影响也是一个新课题。

YAO等[1]介绍了裂纹损伤结构系统的弹塑性分析方法，但由于不涉及断裂力学的内容，事实上只是采用了弹塑性结构力学的分析方法，以致因裂纹而引起的刚性降低，内力再分配无法反映。EI-HADDAD等[2]虽然引入了断裂力学的内容，但因仅局限于线弹性范围的静止裂纹，自然塑性影响无法考虑。BRUST等[3]采用的简便方法，由于其推导基于指数型材料，故难以用于弹塑性增量矩阵法。刘松柏等[4]虽考虑了非静定单一构件边界约束的强弱，但忽略了塑性变形与裂纹撕裂的内在联系，丢失了耦合关系，和文献[3]的结果一样只能是单一裂纹构件的一种近似算法。藤久保昌彦等[5]采用了与文献[2]相似的方法，通过能量释放率将一个特殊的裂纹单元结合到一般的梁柱单元中，虽从中也可考虑裂纹前端塑性修正，但从理论上讲仍应是线弹性小塑性修正解，并且在全塑性条件下与塑性节点理论不协调，需要进行人工干预，不利于完整意义上的计算机处理。

本文研究开发了可用于裂纹损伤结构系统整体计算的新的弹塑性裂纹单元，新的单元为弥补目前已有工作的不足，重点考虑了韧性材料在裂纹前端进入较大范围塑性时的弹塑性影响。本研究利用了SANDERS[6]周向壁穿裂纹弹塑性解析解，通过增量微分，获得了节点内力与位移的显式增量关系，进而建立了弹塑性裂纹增量刚度方程，并将理论结果通过有限元分析方法，形成了一个新的特殊单元，为实现裂纹损伤结构系统的整体分析奠定了理论基础。

2 分析方法

分析模型为柱壳，其中无因次轴向坐标为z，距原点的轴向距离为zR。设材料为理想弹塑性材料，裂纹损伤为周向壁穿裂纹，裂纹长所对的圆心角为2α，裂纹面保持全自由；载荷为施加横截面弯矩，载荷作用方向取使裂纹张开的方向，即保持裂纹处于 Ⅰ 型裂纹破坏状态(图1、图2)。

设参量ε的表达式为:

ε2=(h/R)[12(1-μ2)]-1/2

(1)

式中，μ为泊松比；R为柱壳中面半径;h为板厚。

无因次载荷参数:

(2)

式中，σF为材料的屈服应力;M为作用弯矩。

图1 计算模型

图2 裂纹截面

2.1 基本理论

由于裂纹的存在，在载荷作用下，裂纹截面附近的截面呈较为复杂的应力分布，实验和数值仿真结果[7]表明裂纹在柱壳轴向上的影响有限，应力分布从裂纹截面开始沿柱壳轴方向经过大约1/5～1/4柱壳半长的变化，就基本可收敛到相应条件下的非裂纹柱壳的分布状态，因此从整体上可作为梁考虑，这样上述发生的变化可认为主要是裂纹截面中性轴位置发生变化所致，裂纹和非裂纹截面在中性轴上的差距，形成一个附加的转角。另外，在Ⅰ型裂纹弯矩载荷作用下，在截面拉应力区的裂纹前端将出现拉应力Dugdale塑性长度，即图2中β-α的长度。随着载荷作用，在截面压应力区，将可能出现类似的压应力塑性长度，文献[6]将此称为压应力Dugdale塑性长度，即图2中的π-γ的长度。SANDERS利用壳理论边值解和Dugdale裂纹模型推导了裂纹附加转角理论解，而且结果与轴向z坐标无关，其表达式为：

(3)

式中，Θ为裂纹附加弯曲转角；d可理解为裂纹对圆柱壳柔度的影响，其表达式如下:

(4)

Csinβ=β-α+sin(β-α)-

(5)

πc=-(β-γ+sinβcosβ-sinγcosγ)C-

(π-γ-sinγcosγ)G1+

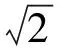
2(sinα-sinβ-sinγ)+(π-γ)+(β-α)cosα+

cosβsin(β-α)-sinγcosγ

(6)

Psinx=Qcosx+β-α-σBsinβ

(7)

Q=-π+γ+σBsinγ

(8)

(9)

(10)

其中，Dugdale拉伸和压缩塑性长度β和γ，从式(11)的超越方程中求解。

(11)

式中，

N1=[sinβ-sinα+(β-α)cosβ]sinx-

N2=[sinγ-(π-γ)cosγ]sinx+

初始，压缩塑性区域不出现时，γ=π，并由式(12)的不等式成立[8]，则只需通过式(11)第一式求出β即可，其第二式此时是自动满足的；当式(12)的不等式不成立时，塑性压缩长度出现，γ<π。

(12)

2.2 裂纹附加转角与弯矩的增量关系

式(3)是反映裂纹影响的主要等式，它不仅包含了裂纹存在的影响，而且由前述可知，裂纹截面的大范围的塑性影响也计入其中，利用该式将可以有效解决本文引言中所提出的问题。由于上述非线性因素，从式(3)～式(11)显然可知，裂纹附加转角与弯矩的关系为隐式，故不宜用矩阵形式表达。另一方面，出于本研究的目的，对于非线性方程求解，运用增量理论是必要的。故这里将推导上述相关公式的增量表达形式。对式(3)进行分析，从Dugdale塑性长度和弯矩的因果关系，可以认为β和γ均应是随σB的变量，可以推导出裂纹附加转角的增量表达式为:

(13)

经整理可得另一种表达方式:

(14)

由上述对β和γ的考虑，同样可对式(11)进行微分计算，从而可得如下表达式:

(15)

将式(15)整理得到:

(16)

将式(16)代入式(14)，消去dβ和dγ组成的向量，可得：

(17)

2.3 裂纹单元增量刚度方程

如图1所示，选择裂纹左右截面分别为i′,j′两节点。利用有限元梁柱理论可以将附加转角与弯矩的关系写成单元刚度方程式的形式，即

(18)

其中，

对于一般梁柱单元，由于刚度矩阵为常量，故其增量形式仅仅将内力和位移向量改为增量写法即可。

就海洋平台结构而言，通常壳长度方向的尺度要远远大于壳截面的最大尺度，因此采用梁单元是一个合理的选择。设如图1所示裂纹损伤的圆柱壳两端节点分别为i和j，在运用有限元计算进行单元划分时，可分为3个单元，第一个单元从柱壳左端到裂纹左截面，为i—i′单元，是一般梁单元；第二个单元从裂纹左截面到裂纹右截面，为i′—j′单元，为本文介绍的弹塑性裂纹单元(注意到该单元与长度无关)；第三个单元从裂纹右截面到柱壳右端,为j′—j单元，也为一般梁单元。

由于上述推导建立在有限元框架体系内，由有限元理论，上述各单元可以进行单元刚度矩阵组装或与全体构件的单元刚度矩阵组装，形成结构整体的总体结构刚度矩阵，然后实施有限元计算。显然，这里包含的是有限元单元族中节点数最少的单元，故形成的未知量也是目前有限元计算中最少的，自然对计算机资源的占用和建模处理等工作量也是最少的，从而使对大型复杂结构系统的整体计算成为可能。

当裂纹截面进入全截面塑性，不难推出有下式成立:

(19)

此时裂纹截面已形成塑性节点。在计算处理上只需将本裂纹单元去掉，然后用塑性节点取而代之，其后将与UEDA等[9]的塑性节点法或YAO的计算[1]构成无缝相接，进一步实施裂纹损伤结构系统的极限分析计算。从理论上讲，两者之间的这一过渡具有一致性，从而回避了由于理论上的不一致所带来的计算上的人为处理，有利于计算机的高效编程和运算。

3 精度的定性分析

从推导过程看，解的误差主要来自SANDERS的理论解，而SANDERS理论解的主要误差来源是壳半膜理论和断裂力学中的Dugdale模型。

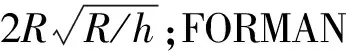
另一方面，来自Dugdale模型的误差主要是因为塑性判断使用的是单轴应力条件,并且忽略了塑性区域沿轴向的扩展，因此所获得的塑性长度常常会偏长，但Dugdale模型巧妙地通过线性结果叠加消除裂纹尖端奇异性的办法实现了对弹塑性非线性问题的求解，避免了复杂数学推导，目前仍是一种公认的非常有效的方法。其误差所带来的结果也是偏于安全的。

在前述整个公式体系中，基本上是对式(3)～式(11)的微分，即是一个正向运算过程，故一般不存在计算上的特别的困难。剩余的计算是增量有限元的常规计算。

4 结 论

本文研究开发了可用于裂纹损伤结构系统整体计算的新的弹塑性裂纹单元，重点考虑了韧性材料在裂纹前端进入较大范围塑性时的弹塑性影响，形成了一个新的特殊单元，为实现裂纹损伤结构系统的整体分析奠定了理论基础。获得了以下结论：

1) 利用SANDERS周向壁穿裂纹弹塑性解析解，通过增量微分运算，获得了内力与位移的显式增量关系。

2) 建立了弹塑性裂纹增量刚度方程，形成了节点或未知数最少的弹塑性裂纹单元，依有限元分析方法，该单元可方便地和结构系统中其它有限元单元进行组合装配并实施整体计算。

3) 定性误差分析表明对于海洋平台的主要结构，其误差为可控。

4) 整个公式体系中，基本上是微分的正向运算，故一般不存在计算上的特别的困难。

5) 该单元的计算可与塑性节点法无缝相接，进行裂纹损伤结构系统的极限分析，实现了两者在理论上的一致性，回避了在计算上的人为处理，有利于进一步提高计算机的计算效率。

作为下一步的工作，该研究将进一步考虑裂纹扩展的影响、扩充组合载荷条件下的单元并且完成该单元的定量精度校核。

[1] YAO T, MOAN T. Elastic-plastic behavior of structural members and systems with crack damage[J]. J. of Soc. Naval Arch., 1987, 161(6): 274-284.

[2] EI-HADDAD M N, RAMADAN O M, BAZARAA A R. Analysis of frames containing cracks and resting on elastic foundations[J]. Intl. J. Fracture, 1990, 45: 81-102.

[3] BRUST F W, GILLES P. Approximate methods for fracture analysis of tubular members subjected to combined tensile and bending loads[J]. ASME J. of Offshore Mechanics and Artic Eng., 1994, 116(11): 221-227.

[4] 劉松柏，安藤柱.き裂とコンプライアンスを有する不静定な配管系の塑性崩壞舉動と終局强度[J].日本機械学会論文集(A編)，1996, 62(5): 1164-1171.

[5] 藤久保昌彦，赵 耀，矢尾哲也.亀裂損傷を有する円筒部材の曲げ崩壞解析[J]. 西部造船学会会報，1991, 82(8): 177-189.

[6] SANDERS J L.Dugdale model for circumferential through-cracks in pipes loaded by bending[J]. Intl. J. Fracture, 1987, 34: 71-81.

[7] 赵耀.裂纹损伤圆柱壳承载能力的实验研究[J].华中理工大学学报，1998, 26(5): 54-57.

[8] SANDERS J L.Tearing of circumferential cracks in pipes loaded by bending[J]. Intl.J.Fracture, 1987, 35: 283-294.

[9] UEDA Y, YAO T. The plastic node method: a new method of plastic analysis[J].Computer Method in Appl. Mech. and Eng., 1982, 34: 1089-1104.

[10] TADA H, PARIS P C, IRWIN G R. The stress analysis of cracks handbook[S]. Del Research Corporation,Hellertown, Pennsylvania, 1985.

[11] SANDERS J L. Circumferential through-cracks in cylindrical shells under tension[J]. J. Applied Mechanics, 1982, 49: 103-107.

[12] FORMAN R G, HICKMAN J C, SHIVAKUMAR V.Stress intensity factor for circumferential through cracks in hollow cylinders subjected to combined tension and bending loads[J].Eng. Fracture Mechanics, 1985, 21: 563-571.