三峡库区船舶碰撞能量损失方法的研究

1 引 言

船舶的碰撞与搁浅是船舶结构重大破损最主要的原因。根据劳氏船级社1995年的统计报告，50%的船舶事故是由碰撞和搁浅造成的。1998年对穿梭油轮的调查发现,70%的原油泄漏事故所造成的海洋污染是穿梭油轮的碰撞与搁浅引起的。综合各种海洋事故统计报告可见船舶碰撞与搁浅是对船舶安全与海洋环境的重大威胁。

三峡库区由于其特有的航道特点和在长江区段中的特有地位，碰撞问题就显得尤为突出。为有效减少事故发生，不但需要提高船员素质、完善监管措施和加强硬件设备，还需要对船舶碰撞机理深入地研究，从而有效地防止通行船舶事故的发生并减少损失。

MINORSKY[1]于1959年揭开了船舶碰撞研究工作的序幕。

PETERSEN和ZHANG[2]基于刚体碰撞力学的一般理论，分析了船舶碰撞过程中的能量耗散问题，并且建立了简化估算公式。

PETERSEN[3]的研究工作具有代表性，他分析了二维情况下的船舶碰撞过程。该方法假设相撞船体只在碰撞点发生相互作用，所有变形均发生在碰撞点附近，并且用非线性弹簧来模拟，船体的其余部分则作为刚体处理。作用于船体上的力包括碰撞力和流体动力，碰撞力假设为撞深的函数，流体动力则采用切片法计算。所建立的船—船碰撞系统数学模型为假定在一个时间步长内，加速度是线性变化的，最终可以求出碰撞力。

梁文娟[4]等考虑碰撞区结构变形的三维特性和船体的六自由度运动，将PETERSEN的二维方法成功地推进到三维。

有限元法是结构碰撞响应分析的一个强有力工具。目前已成功开发了许多非线性有限元商用软件，如LS_DYNA3D、ABAQUS、MSC/DYTRAN、DNV/ADVANCE以及MARC等，这些软件均可用于结构的碰撞分析计算。随着计算机硬件的发展，有限元软件也在向大型化、集成化的方向发展。这也促使有限元的建模和网格划分更加趋于细密，但船舶碰撞数值仿真的建模技术及其在结构耐撞性中的应用目前仍是船舶计算结构力学领域的一个挑战性课题。

2 船舶碰撞能量损失的计算方法

2.1 外部碰撞力学分析理论

外部碰撞力学基于外部动力分析，从动量守恒定理出发，通过解决碰撞过程中两船的刚体运动性能及船与水的耦合问题来估算碰撞能量，以直接计算两船碰撞后的动能损失。本文将基于PEDERSEN和ZHENG[5](1998)碰撞分析理论给出碰撞能量的解析表达式，此运动分析理论中只考虑纵荡、横荡和首摇等3种运动。

2.2 船舶相撞导致船舶变形破损的能量扩散估算

当撞击船冲击被撞船的侧部时，撞击可视为两细长梁的冲击行为。假设具有纵向速度Vax和横向速度Vay的船A撞向纵向速度为Vb1和横向速度为Vb2的船B。为建立系统的碰撞方程(见式(1))，建立如下两个坐标系，其中xyz坐标系是相对于海底的固定坐标系，其中z轴垂直向上伸出静水面，x轴位于船的中纵剖面内并指向船首，坐标原点位于船中底部。ξηξ坐标系里原点位于撞击点C，ξ轴指向撞击面的法线方向，并设x轴与η间的夹角为α，如图1所示。

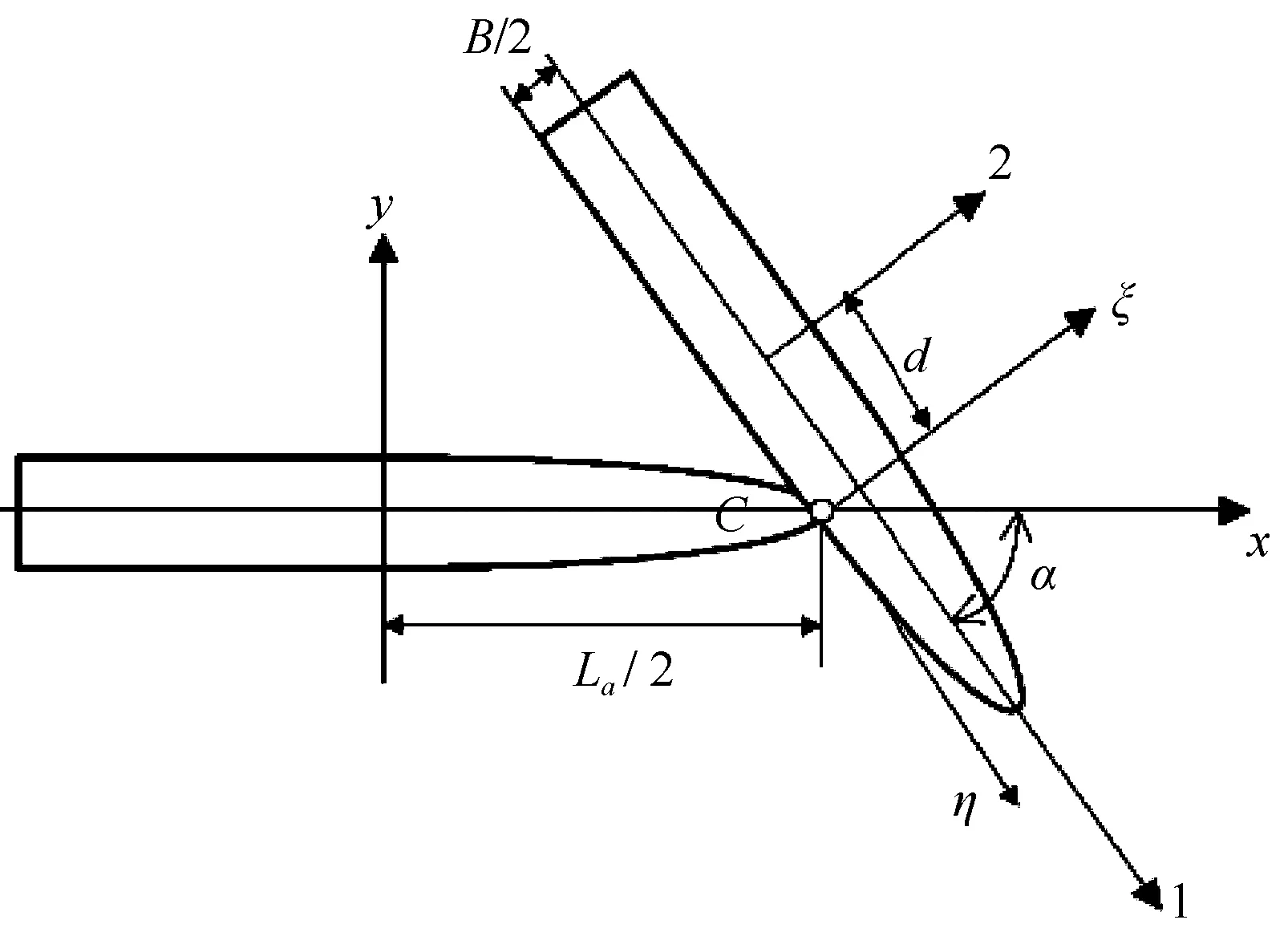
图1 两船相撞的简化图

其中，

(1)

对于撞击后粘连在一起的情况，撞击过程在ξ和η方向的扩散能量分别可表示为：

(2)

式中，

(3)

式中，

系数Daξ,Daη,Dbξ,Dbη,Kaξ,Kaη,Kbξ,Kbη则为：

由此得到相撞后总的能量扩散：Etotal=Eξ+Eη。

2.3 附加质量及其他相关系数

前面的方程中附加质量系数max、may、ja以及mb1、mb2、jb取决于船的外形和冲击历程，可利用水弹性理论并结合切片方法通过数值计算得到。为简单起见，MINORSKY(1959)及MOTORA等(1978)通过水动力计算和一系列的模型实验得到这些系数的经验范围：如may=0.4～1.3，如考虑撞击时间很短，则可取may=0.4。而纵荡的附加质量系数要小于横荡系数，max=0.02～0.07，可取max=0.05,ja=0.21。本文中计算所取的系数max=mb1=0.05，may=mb2=0.4，ja=jb=0.21。

上式中e(0≤e≤1)为恢复系数，本文考虑完全塑性碰撞，即e=0。

2.4 速度变化对能量损失的影响

表1为仅考虑撞击船速度变化，而被撞船静止时，船艏垂直碰撞船舯的能量损失数据。

表1 速度变化时的能量损失数据表

从图2中可见，随着速度的增大，能量的损失也增大。

图2 速度—能量变化数值曲线

2.5 撞击角度变化对能量损失的影响

表2为在仅考虑撞击角度变化时，船艏以10 m/s速度撞击船舯的能量损失数据。

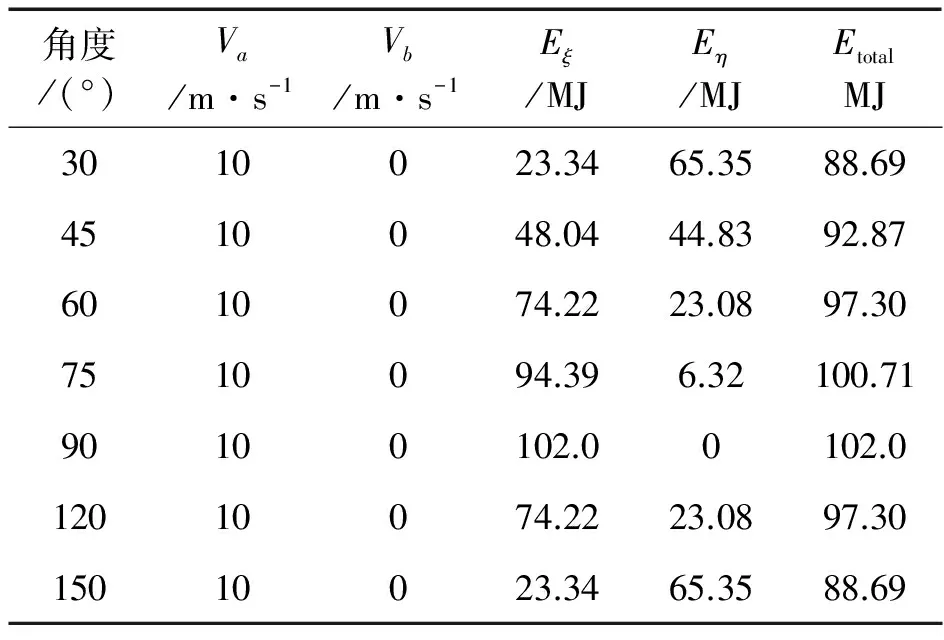
表2 撞击角度变化时的能量损失数据表

从图3可见，船艏垂直碰撞船舯时，能量损失最大。

图3 撞击角度—能量变化数值曲线

2.6 撞击点位置变化对能量损失的影响

表3为仅考虑撞击点位置变化时，撞击船以10 m/s速度与被撞击船垂直碰撞的能量损失数据。

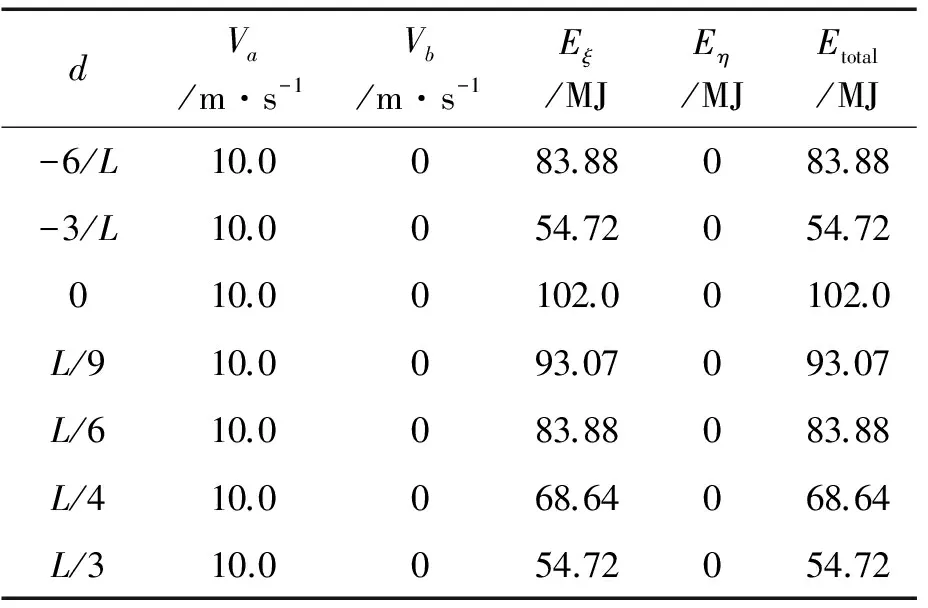
表3 撞击点位置变化时的能量损失数据表

从图4可见，撞击船撞在被撞船船舯时，能量损失最大。

图4 撞击点位置—能量变化数值曲线

3 2 000 t级化学品船有限元模型

3.1 碰撞过程中的环境模拟与模型简化

在一般的船舶碰撞研究中，不论是理论方法还是有限元分析方法，通常只考虑撞击船艏和被撞船船舷其中一方的变形，而将另一方视为刚体，从而大大简化碰撞分析过程。但若从碰撞研究的角度来看，考虑碰撞双方的真实变形和吸能，对船舶碰撞过程进行真实模拟是必不可少的。因此本文将同时考虑撞击船和被撞击船的结构响应。

本文假设2艘相同型号的2 000 t级化学品船发生垂直碰撞，碰撞时船的吃水状态相同，并处于正浮状态。碰撞船以10 m/s的速度撞击被撞船船舯。为了减少建模工作量，缩短计算时间，不必将2艘船的全船模型作为有限元分析的计算模型。

本文将撞击船的艏部和被撞船的舷侧撞击区域处理成可变形结构，作为计算模型，船舶碰撞过程中的非碰撞区结构几乎不发生任何变形，它们的主要作用是作为碰撞区可变形结构的“刚性”边界,并以重量、重心和惯性矩的表现形式影响着相撞船体的运动响应。因此,采用合适的惯性等效方法将这部分“刚性结构”从繁重的建模工作中分离出来是完全必要的,不仅可以简化有限元模型,而且也有助于计算效率的提高。

船体和流体之间的相互作用取决于相撞船舶的型线特征、碰撞历程等。精确的计算是相当困难的。附加质量模型采用船体附加质量的形式来考虑周围流体介质的动力影响，避免占用大量机时的流固耦合计算，显著提高计算效率。在撞击船和被撞船上,需要加上适当的附连水质量。附连水质量采用经验公式确定。

本文中取横漂运动的船体附加质量为:

Myy=0.4M

取进退运动的船体附加质量为:

Mxx=0.05M

其中,M为船舶质量。

3.2 2 000 t级化学品船的主尺度及模型

表4为建立2 000 t级化学品船模型时所用的主尺度参数。

表4 2 000 t化学品船主尺度参数

图5所示为2 000 t级化学品船的几何模型。

为减少建模工作量，本文只建立被撞船的一个舱段，由于舱段对称，仅建立半个舱段研究即可，图6为2 000 t化学品船的半个舱段几何模型。

图5 船艏几何模型

图6 舱段几何模型

3.3 仿真中使用的材料模型

在单元类型的选择上，对于撞击船船艏和被撞击船的舷侧撞击船区域选用hughes-liu壳单元，且沿厚度设置5个积分点，这种单元的特点是消耗更多时间,但处理大变形以及翘曲问题效果更好。非碰撞区域相对来说变形较小，均采用默认的Belytsch-Tsay单元，这种单元求解效率最高，也是LS_DYNA默认的单元类型。

所有单元采用线性随动硬化材料，密度7.8×103kg/m3，杨氏模量E=210 GPa,泊松比ν=0.3,剪切模量ET=1.18 GPa,屈服应力σT=0.235 GPa。

3.4 材料破裂失效准则的选择

在材料失效准则的选择上，本文采用定义失效应变来判断模型失效。本文的失效应变取为0.15。

3.5 材料应变率的考虑

碰撞过程是一个动态响应过程，材料的动力特性影响不能忽略。实践表明，低碳钢的塑性性能对应变率是高度敏感的，其屈服应力和拉伸强度极限随应变率的增加而增加[7]。船体结构材料大多属于低碳钢, 而船舶碰撞又是一个瞬态过程, 材料的应变率是比较大的, 所以,在船体结构碰撞分析中考虑材料应变率敏感性的影响是完全必要的。 本文在材料模型中采用cowper-symonds本构关系。

(4)

3.6 接触的定义

接触问题的处理是船体结构碰撞计算中重要而困难的部分。碰撞过程中，接触边界是不断变化的，计算中必须不断地对接触边界进行搜寻。以往所作的碰撞过程分析一般采用的都是面与面的主从接触，这要求对结构有可能发生的接触现象有所把握，并且做到没有遗漏，避免定义不可能发生的接触。显然这样大大增加了处理问题的复杂性。单面自动接触广泛应用于汽车碰撞分析中，它将自动从壳单元的两边进行接触检测，不用人为定义主、从接触面，所以适合各种复杂的接触行为。因此，本文中的接触定义为单面自动接触。

4 仿真计算结果与分析

4.1 船舶碰撞过程情景描述

本文计算的碰撞时间为0.5 s。两船碰撞0.18 s时刻如图7所示。

图7 碰撞场景

撞击船与被撞击船由于吨位与吃水状态相同，起初两船处于同一水位上。随着碰撞过程的进行，与外壳舷侧结构发生碰撞的首先是水线上方艏柱前倾部分，撞击船的艏柱部分已经切入到了被撞船的外壳舷侧内部。碰撞过程继续进行，随着船艏的继续深入，船艏的尖头部位与被撞船的内壳舷顶列板发生碰撞，并且尖头切入内壁，最终将会穿破上甲板。值得注意的是，碰撞使撞击船艏在船长方向发生了倾斜。在真实的侧向垂直碰撞时，撞击船也会发生纵向倾斜。

4.2 船艏结构损伤变形

船艏结构变形不大，艏部外板发生了一定程度的屈曲变形，与船侧结构直接碰撞的区域发生了较大的压溃变形,如图8所示。

图8 船艏压溃图

4.3 舷侧结构损伤变形

舷侧结构的损伤变形具有局部性，基本集中在碰撞区域。直接与船艏相撞的船侧及上甲板部分发生了很大变形，并且出现破裂。如图9所示，外壳的舷侧外板发生了拉伸变形，上端已经被船艏切开了一个裂口。由于船艏的特殊性，在船艏还没有完全穿透双层壳时，船艏的尖头部位已经与内壳的舷顶列板发生碰撞，最终将穿透上甲板，导致灾难性的后果。

图9 舷侧与上甲板破裂图

4.4 能量损失分析

如图10所示，撞击船起初具有177 MJ的动能，在0.1 s之前两船还没有相撞。在碰撞发生后0.1～0.5 s之间动能开始急剧减少，直到0.5 s时动能已经减少到165.65 MJ,此时动能损失了11.35 MJ。

如图11所示，撞击船起初内能为0，内能从0.1 s开始急剧增加，到0.5 s时内能增加到3.35 MJ。

如图12所示，被撞击船起初动能为0，动能从0.1 s开始急剧增加，到0.5 s时动能增加到1.01 MJ。

如图13所示，被撞击船起初内能为0，内能从0.1 s开始急剧增加，到0.5 s时内能增加到2.91 MJ。

图10 撞击船动能曲线示意图

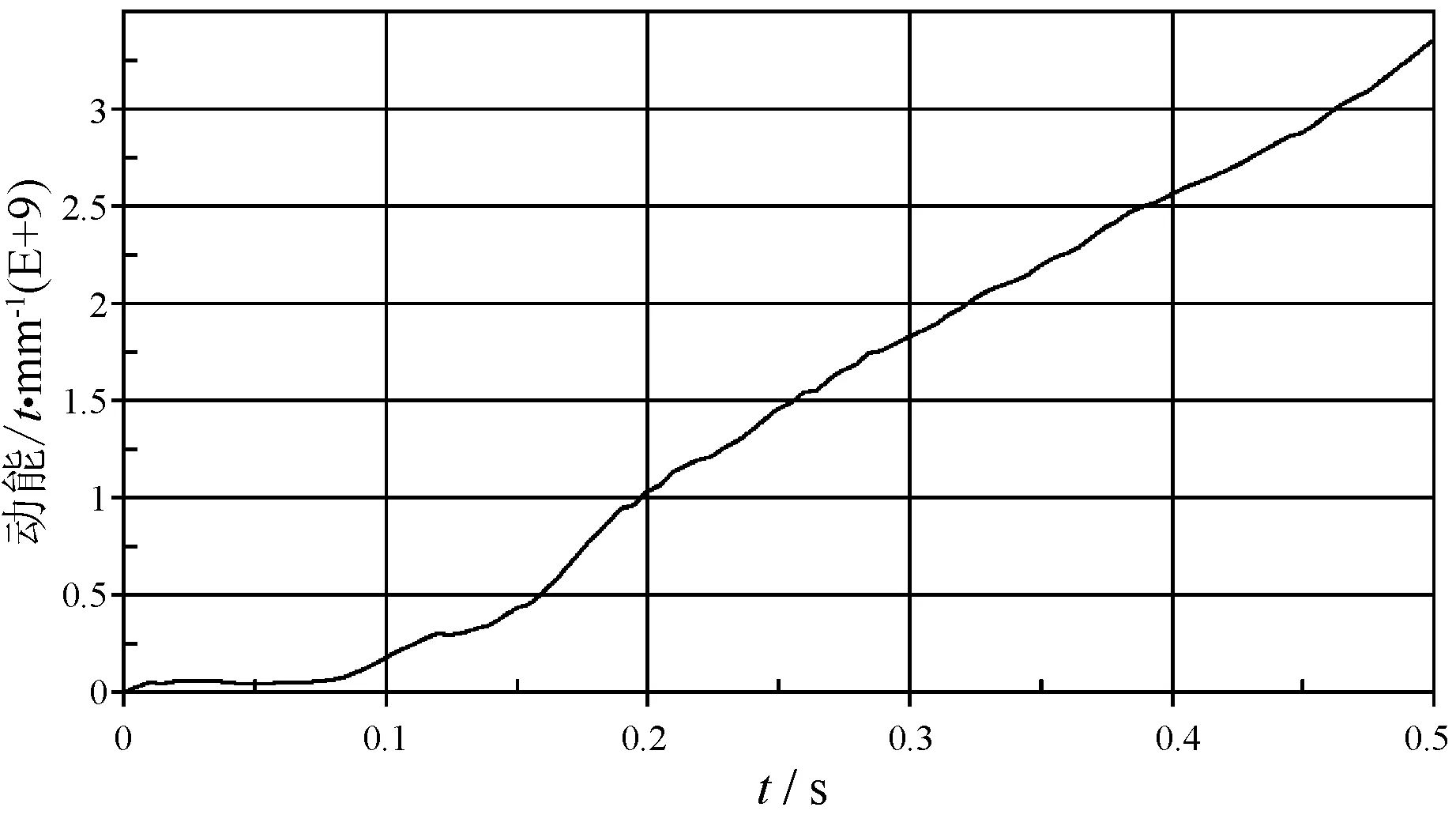
图11 撞击船内能曲线示意图

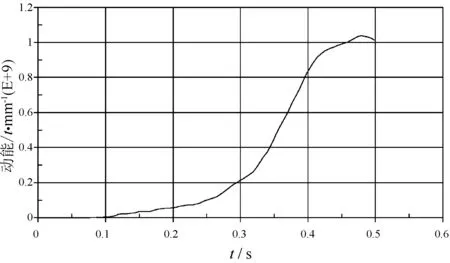
图12 被撞击船动能曲线示意图

图13 被撞击船内能曲线示意图

表5能量形式转换数据表

序号能量转换形式能量值/MJ比例/%1撞击船内能3．3529．502被撞击船内能2．9125．603被撞击船动能1．018．904摩擦能、沙漏能等4．0836．005动能损失总计11．35100

由表5可见，撞击船损失的动能主要转换为两艘船的内能，很少一部分转换为被撞船的动能。船艏吸收的能量和舷侧所吸收的能量相当，以往将船艏视为刚体的方法偏于保守，不能反映真实的情况。

4.5 各构件吸能能力

由表6可见，船体外板吸收了大部分能量，是吸收能量的主要构件。

表6 船艏各构件吸能数据表

图14所示主要是船艏的外板、甲板、龙骨、强横梁等吸收能量的状况。

图14 船艏各构件吸能图

由表7可见，舷侧外板吸收了大部分能量，是吸能的主要构件。

图15所示主要是舷侧外板、 上甲板、 内壁板、 强肋骨、强横梁等吸收能量的状况。

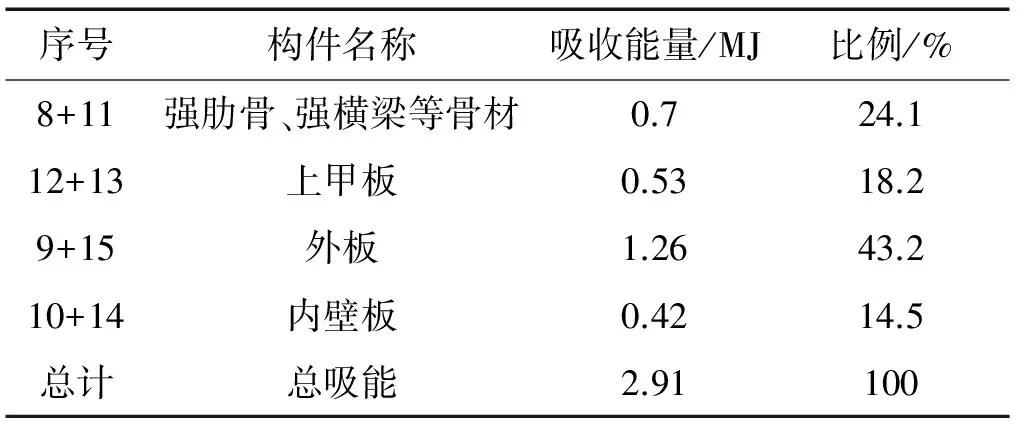
表7 舷侧各构件吸能数据

图15 舷侧各构件吸能图

5 结论与建议

船舶碰撞类型按照船艏形状可以分为水下撞击和水上撞击。以往的文献通常研究的都是水下撞击，即撞击船船艏为球鼻型艏。由于三峡库区化学品船船艏为前倾型艏，因此研究水上撞击是必要的。所以在评价三峡库区化学品船碰撞损伤标准时，应注意以下几点：

1) 外部碰撞力学分析理论能够简单快速地评估碰撞能量损失的大小，但是不能详尽反映碰撞的复杂过程，有其局限性。有限元仿真能够详尽模拟碰撞的复杂过程，并能全面反映能量转换的情况，但是建模工作量大，效率不高，受到时间的限制。所以，在评估碰撞能量损失的大小时，建议将两种方法有机结合起来。

2) 以往的文献通常将船艏视为刚体，这是因为舷侧的吸收能量要远远大于船艏的吸收能量。但是也有相关文献报道如PEDERSEN提到的某些型式的船艏吸收的能量将会大于被撞船舷侧吸收的能量[8]。所以为了反映真实情况，应该考虑两者同时吸能的情况。

3) 以往的评价标准通常是不允许双壳舷侧结构的内壁板发生断裂破坏，而由于三峡库区的化学品船船艏的特殊性，碰撞在未穿透内壳之前可能先导致上甲板破裂，同样会造成化学品的泄漏，所以对于此类碰撞需要区别对待。

参考文献:

[1] MINORSKY V U. An analysis of ship collision to protection of nuclear powered plant[J].Ship Research,1959(1):1-4.

[2] PETERSEN P T, ZHANG Shengming. The mechanics of ship impacts against bridges[C]∥Proceedings of the Int.Symp on Advances in Ship Collisim Analysis. Copenhagen:Technical University of Demark,1998:41-51.

[3] PETERSEN P T.Dynamics of ship Collisions[J].Ocean Engineering, 1982, 9(4):295-329.

[4] 梁文娟,金允龙,陈高增.船舶与桥墩碰撞力计算及桥墩防撞[C]∥中国公路学会、桥梁和结构学会.第十四届全国桥梁学术会议论文集.上海：同济大学出版社，2000:566-571.

[5] ZHANG Shengming.The Mechanics of ship collisions[M].Lyngby:Department of Naval Architecture and Offshore Engineering, Technical University of Denmark,1999.

[6] 王自力，顾永宁.应变率敏感性对船体结构碰撞性能的影响[J].上海交通大学学报，2003，34(12):1704-1707.

[7] 赵海鸥.LS-DYNA动力分析指南[M].北京：兵器工业出版社,2003.

[8] SAJDAK J A W,BROWN A J.Modeling longitudinal damage in ship collisions,SSC Report SR-1426[R].Blacksburg,VA:Department of Aerospace and Ocean Engineering,Virginia Polytechnic Institute and State University,2004.